网站首页  词典首页

请输入您要查询的论文：

　

标题 基于元胞自动机双车道混合车辆变道规则的交通流模型研究
范文 王婷++周石鹏



摘 要：针对车辆行驶的交通流问题，兼顾现实中的多车道及车辆性能差异两个问题，在开放性边界的条件下，将基础的STCA模型进行改进，建立对称双车道大小车变道元胞自动机模型。文章核心在于变道规则的演化设计，根据逐步改进的变道规则，模型分为三种：模型一，大、小车都不允许变道；模型二，小车允许变道但同时不允许超车，大车不允许变道；模型三，小车既可以变道又可以超车，大车允许变道不允许超车。利用Matlab软件进行计算机仿真模拟，得到三种模型的时空斑图，图形结果显示：在保证安全性的前提下，车辆的变道、超车行为在改善交通状况的方面确实起到了很大的作用，堵塞相变少，同步流得到提升，道路利用率得到了提高，较STCA模型模拟的交通流更接近现实，也更具有指导意义。
关键词：交通流；元胞自动机；双车道；混合车辆；变道规则；仿真模拟
中图分类号：F570 文献标识码：A
Abstract： In the open boundary condition， by improving the basic SCTA model， paper established a cellular automaton of hybrid vehicle in symmetrical two-lane. The care of this paper is the evolutionary design of lane changing rules. According to the improved lane changing rules， the model is divided into three types. Model Ⅰ： lager and small vehicle are not allowed to change lanes. Model Ⅱ： the small cars are allowed to change lanes but not allowed to overtake； the large cars not allowed to change lanes. Model Ⅲ： the small cars are allowed to change lanes and to overtake； the large cars are allowed to change lanes but not allowed to overtake. Taking advantage of Matlab software to simulate， models obtain three types of space-time figure. On the premise of safety， the result display the behavior of changing-lane and overtaking in improving the traffic situation has indeed played a big role. It is shown that the congestion is less， the synchronous flow is improved， and the road utilization rate is promoted. This model is closer to reality and more instructive than STCA model.
Key words： traffic flow； cellular automation； two-lane； hybrid vehicle； lane changing rule； simulation
0 引 言
汽车代步确实给我们的生活带来了诸多的方便，但随着其数量井喷式的增长，给我们的交通状况带来了前所未有的压力。每逢节假日的高速公路，甚至是在普通工作日，我们城市的高架、公路都被填的水泄不通。车辆行走缓慢、容易发生交通事故，这种状况屡见不鲜。早在20世纪中叶开始，交通问题就成为了社会关注的热点问题[1-2]。合理准确的交通流模型，能够给驾驶员、道路规划机构一些科学的参考和建议。交通系统本质上属于离散的系统，且具有很多非线性特性。元胞自动机模型（Cellular Automaton Model，CA）能够有效模拟交通流的微观运动，较好地揭示交通流从自由运动相到局部堵塞相的转变，成为研究交通流的重要模型之一，且被广泛应用。最初人们发现184号CA规则最符合单车道的交通流模拟，车辆随机分布在一维离散的元胞链上，每个元胞只能被一辆车占据或者被空闲下来，每辆车所在元胞位置就是其在公路上对应的坐标，且具有各自的速度。每个元胞上车辆之间产生相互作用，它们根据自身状态及邻域元胞上车辆的状态选择下一步长的运动：加速、减速、随机慢化。到了1992年，Nagel和Schreckenberg提出了著名的NaSch模型[3]，随后的学者在此启发下，不断改进模型的规则以及参数[4-16]，使其模拟结果更接近现实交通流状况以及能够给出更为具体的建议，即后期陆续提出的STCA模型、VDR模型、T2模型、BJH模型等，这些模型将双车道变道、交通的亚稳态、回滞、驾驶员行为、前车状况等特殊现象考虑进来，实施进一步地研究分析。
按照对交通流细节描述的不同，交通流模型分为三种，分别为：微观交通流模型、中观交通流模型、宏观交通流模型。本文站在微观的角度，主要研究混合车辆在双车道变道过程中对整个交通系统产生的影响。大、小车具备不同的性能，在操作简便、视野开阔、加速制动性能良好等方面来看，小车最优、大车其次、障碍车最差。也正是因为每类车辆性能的不同，使得它们在直线行驶、变换车道过程中存在速度快慢、操作实施难易程度的差别，进而对道路交通的影响程度存在差异。因此在双车道模型中仅仅考虑车辆的变道规则是不夠的，还要将车辆自身性能区分开来，使得最终的仿真模拟更贴近实际情况，也更具有现实指导意义。
1 模 型
现实生活中均是多车道的道路，本文以双车道为例进行交通流的仿真模拟，后续可以延伸到更多车道情况下。考虑到车辆自身性能的差异以及模型的简洁易懂，本文将车辆分为小车、大车两类型，他们分别代表了性能优、劣两个等级车的种类。小车在制动、加速方面更为迅速，在变道过程中更为灵活，因此在设定变道规则时也要区分车的种类，这样模拟出来的结果才会更贴近现实。
按照双车道制定两条平行的元胞链，将这两条元胞链都均匀分割成500个元胞，每个元胞最多只能同时被一辆车占据。在元胞自动机模型中，每个元胞依旧采用以往的经验：对应道路7.5m的数值长度，则模拟的实际道路长度为3.75km[8]，边界为开放性边界条件。
1.1 变道模型。模型在时间和空间上都是离散的，道路的初始化状态：车辆随机地分布在元胞长度为500的一维离散元胞链上，每个元胞在一个步长时间内只能被一辆车占据或者被闲置。v■、x■、d■分别表示车辆在时刻t的速度、所处元胞位置及车间距。其中v■∈0，1，2，…，v■，这里的v■分为大小车最大速度两个等级：v■表示小车的最大速度，v■表示大车的最大速度。R■表示小车在每条元胞链上车辆总数中所占的比例，R■对应大车的比例，l表示随机慢化概率。
根据STCA模型原型的改进，变道规则如下所示：■
其中：d■表示与邻车道前方车辆之间的元胞数，d■表示与邻车道后方车辆之间的元胞数，d■表示足够允许车辆变道的元胞数临界值。
d■d■表示邻车道行驶条件较好，第i辆车的驾驶员接收到可以变换车道的信息。d■
>d■为安全条件，表示第i辆车变道不会造成对邻道上后面车辆的堵塞。
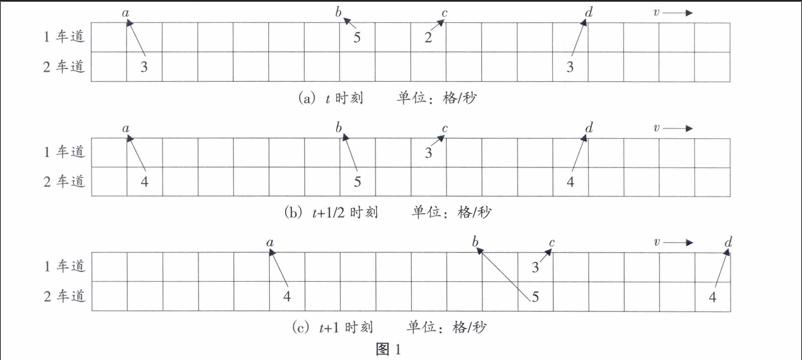
在STCA模型中d■取v■，但是这个条件过分严格，使得原本可以进行变道的车辆因为此严格条件的限制而无法完成变道，大大缩减了道路的利用率、减小了车流量。在本文计算机模拟时，定义d■=1+v■-v■x■-j+1，在保证安全的前提下改善过去严苛的要求，拓宽了变道的条件，这在很大程度上提高了道路的利用率，车流量也会随之增加。下面以图形的形式演示双车道车辆变道的过程，如图1所示。
1.2 变道规则的细化。在本文中，车辆种类的不同需要设定不同的变道规则，将车辆变道模型分为三种情况来研究。
（1）小车、大车都不能变道，只能在各自的道路上自左向右行驶。
在这种情况下，所有车辆完成加速、减速、随机慢化三个过程，完成一个步长时间内空间与速度的更新。其中加速、减速、随机慢化的规则如下。
①加速过程。车辆完成加速需要遵循的表达式为：v■a■-j+1=minv■a■-j+1+1， v■， j∈1，2，…，j。
②减速过程。在减速之前，首先要计算出车辆与同道前方车辆的车间距，计算公式如下：d=k-a■-j+1。
其中：k表示第i辆车同道前方车辆的位置。
然后，完成减速过程，遵循公式如下：v■a■-j+1=minv■a■-j+1+1， d， j∈1，2，…，i。
③随机慢化。第i辆车的驾驶员能够根据自身驾驶经验结合前方道路的状况做出减速的判断，称这一过程为随机慢化。本文使用Matlab软件进行编程，基本理论如下。
定义一个随机慢化的函数randslowv；
确定一个慢化概率prob_slow=l，在本文中l取0.3；
产生一个随机数u，若u≤l，则v■=maxv■-l， 0。
当所有车辆完成上面三个步骤，都会更新自己的状态，产生一个新的速度值和位置坐标。
（2）小车允许变道，大车不允许变道。在这个原则下，必须区分小车、大车，若是小车，则先完成加速过程，再根据变道规则选择是否变道，上文中已经详细说明变道规则，在此不再赘述。若满足变道条件，完成转换车道的步骤；若不满足，则在原本的车道上完成减速、随机慢化步骤。当然，这里还要控制在时刻t已经完成一次变道的小车，在时刻t+1不能再连续变道，这种情况在下文中的第三种情况中进行分析。对于大车则实施与第一种情况相同的行驶状态。最终，实现车辆在空间与速度上的更新。
（3）小车、大车均允许变道，小车允许连续变道，也就是所谓的超车行为，但是大车不允许连续变道。在此原则下，同样需要区分小车、大车，但是与第二种情况不同的是，再次放宽了变道条件，大小车都允许发生变道行为，并且小车允许连续变道，即实现超车，但是大车不能实现连续变道。具体的变道规则、加速、减速、随机慢化均与情况一、情况二相同。
最后，为了验证模型的合理性及说服力，加入障碍车。障碍车包括车辆的物理尺寸笨拙、加减速性能差、驾驶员反应迟缓等严重影响交通流效率的车辆种类。当车辆遇到前方是障碍车时，只要满足变道条件，就可以发生变道，结合理论和实际，这样可以大大提高交通流的效率。
2 数值模拟和分析
设定道路的初始化状态，双车道分割成500个等份的元胞格点，车道边界为开放性边界，将车辆按照一定的比例r随机分布在元胞链上，在本文中r取0.3，小车、大车的分配比例分别为R■=4/5、R■=1/5。参照《中华人民共和国交通安全法》的规定，定义小车最大速度v■=5、大车最大速度v■=3。即小车每秒可通过5个元胞格点，对应实际车速135km/h；大车每秒可通过3个元胞格点，对应实际车速81km/h。车辆在随机慢化过程中，定义慢化概率l=0.3，再随机产生一个随机数0≤u≤1。若u≤l，则进行慢化操作v■=maxv■-1，0，否则不实施慢化操作。
本文采用Matlab软件进行仿真模拟，根据变道規则的不同分为上文中提到的三种情况进行研究分析，具体的模拟结果在下文中将做出具体的阐述。
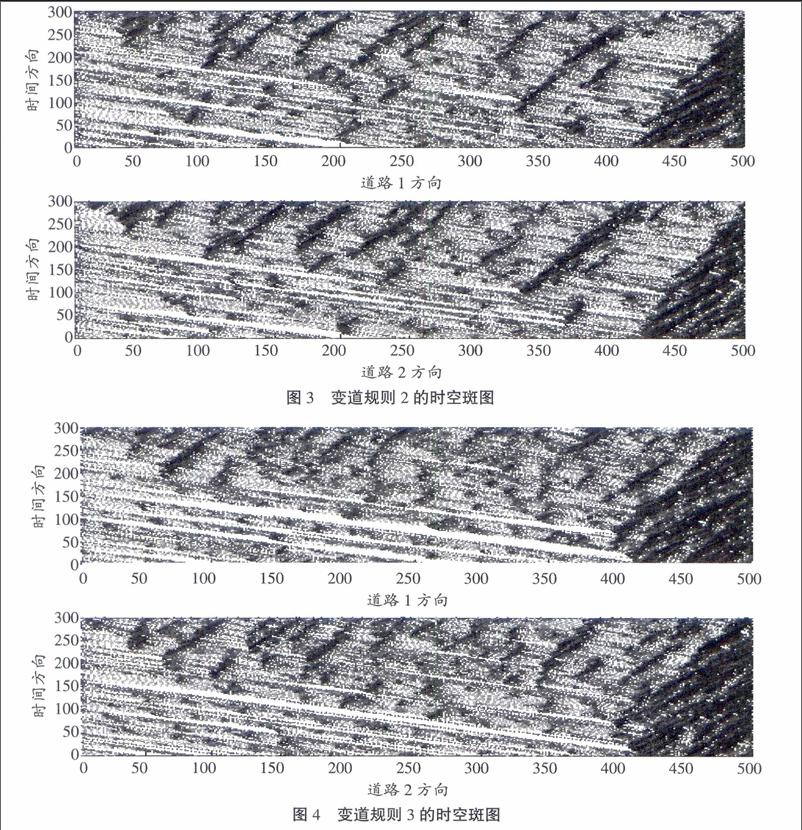
（1）变道规则1：小车、大车都不允许变道。在这种情况下，所有类型的车辆只能在各自原始的车道上自左向右行驶，不能转换行驶车道。这种规则严重阻碍了车流量、速度，致使道路资源的大大浪费。模拟的时空斑图如图2所示。
（2）变道规则2：小车允许变道且不允许连续变道，大车不允许变道。在这种情况下，所有大车只能在各自原始的车道上自左向右行驶，不能转换行驶车道。与变道规则1比较，在此规则2中，拓宽小车的变道条件，允许小车发生变道行为，但是禁止小车连续变道，也就是不能完成超车行为。采用Matlab模拟，得到的时空斑图如图3所示。
如图2、3所示，规则2中堵塞相明显比规则1中的减少很多，车辆同步流提升较大，同时道路资源的利用率也得到了较大提升。
（3）变道规则3：小车、大车都允许变道，小车允许连续变道，但是大车不允许连续变道。在这种情况下，所有车辆都允许采取变道行为。与变道规则2比较，再次拓宽了车辆的变道条件，允许小车变道且能够连续变道，完成超车行为，但是大车考虑到安全的因素，况且自身性能的限制不能完成超车。采用Matlab模拟，得到的时空斑图如图4所示。
如图4所示，交通流的拥堵相再一次明显减少，说明车辆的变道、超车行为在改善交通状况的方面确实起到了很大的作用。本文模型的模拟结果能够给实际交通规划提出一个科学合理的参考。
3 结 论
本文针对双车道，将车辆自身的不同属性作为切入点，根据车辆的操作简便、视野开阔、加速制动性等方面将其区分为大车、小车。结合CA交通流仿真模型，重新定义大车、小车的行使和变道规则，运用Matlab进行编程，具体呈现出三种演化结果。
（1）规则1：大、小车都不允许变道，只能在各自原本的车道上行使，通过时空斑图可以看出堵塞相较多，车辆行驶缓慢，同步流较少，造成道路资源很大的浪费。
（2）规则2：大车不允许变道，小车允许变道却被限制超车行为，其时空斑图呈现出堵塞相明显减少，同步流提升，道路资源的利用率得到了较大提升。
（3）规则3：大、小车都允许变道，小车允许超车，但大车不允许超车，其时空版图显示堵塞相再一次明显减少，道路资源逐渐得到了充分地利用。
在保证安全性及合理性的前提下，将演化规则一步步改进，模拟结果也更加理想且逼近现实。车辆的变
道、超车行为在改善交通状况的方面确实起到了很大的作用，本文模型的模拟结果能够给实际交通规划提出一个科学合理的参考。
参考文献：
[1] Wolfram S. Statistical Mechanics of Celluar Automata[J]. Review of Modern Physics， 1983，55（3）：601-644.
[2] Li X B， Wu Q S， Jiang R. Cellular Automaton Model Considering the Velocity Effect of a Car on the Successive Car[J]. Physics Research E， 2001，64（1）：128-132.
[3] Nagel K， Schreckenberg M. A cellular automaton model for freeway traffic[J]. Journal de Phys. I France， 1992，12（2）：2221
-2229.
[4] CHMURAA T， HERZB B， KNORR F. A simple stochastic cellular automaton for synchronized traffic flow[J]. Physica A， 2014（405）：332-337.
[5] AL-KAISY， DURBIN C. Platooning on two-lane two-way highways： an empirical investigation[J]. Procedia Social and Behavioral Sciences， 2011（16）：329-339.
[6] CHMURAA T， HERZB B， KNORR F. A simple stochastic cellular automaton for synchronized traffic flow[J]. Physica A， 2014（405）：332-337.
[7] 刘应东，牛惠民. 多站台港湾式公交站交通流模型及仿真分析[J]. 交通运输系统工程与信息，2012，12（5）：97-102.
[8] 王永明，周磊山，吕永波. 基于元胞自动机交通流模型的车辆换道规则[J]. 中国公路学报，2008，21（1）：89-93.
[9] 郑容森，谭惠丽，孔令江，等. 开放边界双车道混合车辆交通流的研究[J]. 广西师范大学学报（自然科学版），2005，23（2）：1-4.
[10] 李兵强，钟诚文，牟勇飚. 基于安全效应的双车道元胞自动机交通流模型研究[J]. 交通與计算机，2007，25（136）：27-30.
[11] 冯树民，聂涔，胡宝雨. 基于元胞自动机的高速公路货车结伴行为研究[J]. 交通运输系统工程与信息，2016，16（5）：97-103.
[12] 彭麟，谭惠丽，孔令江，等. 开放性边界条件下双车道元胞自动机交通流模型耦合效应研究[J]. 物理学报，2003，52（12）：3007-3012.
[13] 刘应东，牛惠民，王建强. 考虑安全移动距离的交通流元胞自动机模型[J]. 计算机工程，2015，41（6）：18-23.
[14] 吴可非，孔令江，刘慕仁. 双车道元胞自动机NS和WWH交通流混合模型的研究[J]. 物理学报，2006，55（12）：6275-6280.
[15] 沈泉飞，曹敏，董玉军. 基于粒子群算法的矢量元胞自动机转换规则获取[J]. 现代测绘，2015，38（3）：11-14.
[16] 邱小平，于丹，孙若晓. 基于安全距离的元胞自动机交通流模型研究[J]. 交通运输系统工程与信息，2015，15（2）：54-60.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 11:40:28