《初中数学概念教学中不同概念类型的应对策略》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

初中数学概念教学中不同概念类型的应对策略

范文

孙洪波吴晗

【摘要】学生的培养要从根上抓起，数学概念是数学基础理论的重要组成部分，在学生分析、理解和吸收数学的基本原理、基本规律过程中有着举足轻重的地位.因此，数学概念教学是数学基础教育的核心内容.数学概念特点鲜明，本文针对数学概念存在的问题，分析数学概念的特征，结合初中生的心理认知特点，提出了不同概念类型的应对策略，从而帮助学生更好地认识数学概念，理解数学概念和应用数学概念解决问题.

【关键词】初中;数学;概念;策略

数学的研究对象是事物的数量关系和空间形式，这种关系和形式脱离了事物的具体物质属性，而数学概念有与之相对应的特点.数学概念是人脑对现实对象本质特征的一种反映形式，也是一种数学的思维形式.数学中通常用定理、法则、公式等表达一般思维形式的推理和判断，而数学概念恰恰是定理、法则、公式等的基础，所以，正确理解数学概念是掌握数学基础知识、运用数学运算技能、发展逻辑论证和提升空间想象能力的前提条件.

一、当前初中数学概念教学的教与学都存在一些问题

一、教师层面

一些教师对课程标准的重要性认识不足，没有深入研究，对概念的讲解不到位，因此，在实际授课过程中，教师无法向学生具体、全面地讲授对数学概念的理解，甚至可能传授一些错误的数学概念理解.这种问题的存在，对学生掌握数学基础知识和基本技能的影响是非常负面的，学生学习数学知识的有效性就要大打折扣.特别是当学生碰到综合题目时，学生经常因为数学概念不清晰，读不懂题，理解不全题意而不能将题目正确解答出来.如果教师不改变教学模式，不注重概念教学，一味地让学生刷题，实现知识的“全覆盖”，就会不利于对学生数学创新能力的培养，学生很难适应未来激烈的竞争.

（二）学生层面

数学试卷考题一般不会直接考数学概念的定义，而是在试题中间接考查学生对基本概念的理解，如果学生对概念学习感到枯燥乏味、兴趣不高，那么对概念的理解也不会深刻，从而影响其数学思维的开发.一些学生在学习新内容时，对数学概念死记硬背，忽视了概念的生成过程，填鸭式地被动接受，不求甚解，这样不但不知其然，更不知其所以然，没有真正理解数学精髓，后期解题更难以灵活应用，不能揭示相关概念的本质属性.

针对数学概念教学存在的问题，本文分析了数学概念的特征，有的放矢地进行研究.有些数学概念既是某种对象的性质，又是某种对象的判定，性质特征让我们认识了概念的内涵，而判定特征让我们明白了概念的外延.有些数学概念具有指导性特征，它指出了某种数学操作过程，如“中位数”概念，它指明了寻找中位数的操作方法;有些数学概念交代了对象的形式特征，如“分式”“二次根式”，概念中带有“形如”字样的都属于这一类;有些数学概念是具体的，指向清晰明了，而有些数学概念是抽象的，需要细致琢磨;有些数学概念是相对的、发展的，在不同阶段学到的是不一样的，但纵观知识体系又是不断递进的，如“函数”;有些数学概念具有很强的系统性、关联性，并非独立存在.如果学生对概念的定义、形成过程理解深刻，那么将有助于他们灵活地运用相关数学概念解决生活中的数学问题.如果学生生搬硬套，忽视概念间的相互关系，未能将它们有机结合，概念间无法构成系统，学生在解题时就不能有敏捷的思维，甚至会出现知识上的断层，更谈不上灵活解题.

二、不同概念类型的应对策略

（一）简单概念与复杂概念

有些数学概念通俗易懂，无须过多解读，学生就能接受、理解.例如，正数、负数、多项式、同类项等，这样的概念属于简单概念.对于简单概念的教学，教师可以指导学生从生活实际出发，创设情景，通过与生活的实际感知，从自身的实际体验中抽象提取出相关的简单概念.例如，教师在教学四边形时，对于平行四边形的概念、矩形的概念、菱形的概念及正方形的概念，学生很容易从生活中得到图形原型，自然对概念掌握起来更具形象化，容易理解，对后续特殊四边形的性质与判定的学习也大有帮助.

对于复杂的数学概念，教师应该与学生一起搜寻相关的教学情景，提炼实例中体现的数学特征，概括本质属性，得出概念.在剖析概念时，教师要对正例与反例做出恰当的组合.当学习复杂概念时，具体的例子显得尤为重要.学生不仅要从正例中获得信息，而且要从反例中获得信息.复杂概念的表达一般会由文字语言和符号语言共同描述，教师要在教学中善于抓住复杂概念语句中的核心关键词，引导学生反复推敲，深入理解.以概念中的关键词为抓手进行教学，可以有效地加强学生对概念的准确把握.

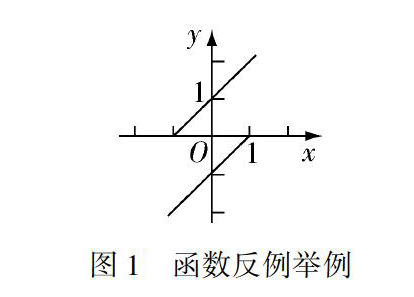
下面以“函数”概念的学习为例，阐述复杂概念的教学策略.对于初中学生来说，函数是一个非常复杂的概念，教师在教学时要不断地给出具体的生活实例，或者可以让学生模仿教师找到一些实例，如某一天的气温变化图、根据年龄与身高绘制的表格、速度不变时路程与时间之间的关系等.教师引导学生发现每一个例子中都含有两个变量，它们之间具有某种特定的关系，而这种关系就是函数关系.学生会总结出“一個量变化，另一个量也随之变化”，这时，教师可以告诉学生“y=1（x为任意实数）”也是一个函数关系，从而引导学生修正对函数概念的认识为“一个量确定下来，另一个量也随之唯一确定下来”，从而得到函数的概念.在这之后，教师对概念进行辨析，不但要有正例，而且要有反例，如图1所示，当x=0时，y有两个值（-1，+1）与之对应，函数值不唯一.通过正反例举例，学生可以进一步更好地理解函数概念.

图1函数反例举例

（二）具体概念与抽象概念

对于具体概念，特别是直观概念，在初中数学概念教学中，借助图形、形象认识、数形结合始终在数学概念的掌握中起着重要的作用.特别是对于初中生来讲，他们的抽象概括能力还不高，对事物的认知还停留在具体事物阶段，所以借助图形学习概念是非常必要的.例如，在学习函数的概念时，学生借助函数图形会对概念的认知达到一个更深的层次.下面以“一次函数”为例.

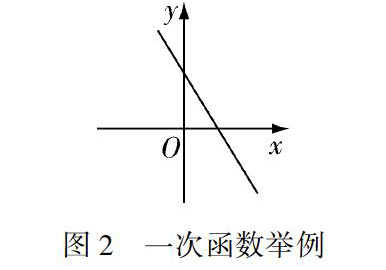
一般来说，形如y=kx+b（k，b是常数，k≠0）的函数，叫作一次函数.这是一个非常具体的概念，只要是照着这个形式给出的函数就是一次函数，但只是照搬形式，还是不能很好地理解究竟什么是一次函数，这时对一次函数图像的研究就显得尤为重要.通过列表、描点、连线，学生会发现一次函数的图像是一条直线，直线的升降趋势受k控制，直线与y轴交点的位置受b控制.当k<0，b>0时，一次函数图像如图2所示.这样由解析式结合图像就能让学生更深层次地理解一次函数的概念.

图2一次函数举例

对于抽象的数学概念的处理，教师应先了解学生的认知水平，从实际生产、生活的经验中寻求贴切的具体实例进行引入，由熟悉到陌生，有助于化抽象概念为具体概念，特别是概念引出阶段，顺其自然，思维无突变，有利于学生对抽象概念的理解.以概率的定义为例，对于初中学生来说是抽象的、难以理解的，但是通过抛掷硬币的实验游戏，教师让学生明白了抛掷硬币有两种可能性，每种可能性的概率都是0.5.通过具体事例变抽象为具体，学生亲身感知并了解了概念，加深了对概念的认识，这是解决这类概念教学的好方法.

（三）关联概念与类比教学

在初中数学教学中，对其中涉及的相关概念进行类比及有机联系是非常必要的，既能起到复习的作用，又能全面深入地联系各个相关概念，训练学生的整体思维能力.数学中的概念众多，相互间有着密切的联系，如分数与分式、全等三角形与相似三角形、方程与不等式等，教师在教学时应善于发现它们的相同点与不同点，以确保学生能够掌握概念的本质，将新概念纳入已有的知识体系中，巩固思维导图.

对于初中的数学概念，概念之间不仅存在一定的纵向联系，还存在一定的横向联系，如何掌握好这些概念的相互联系，教师应当引导学生自主地加以辨别概念间的差异，寻求概念之间的沟通及联系，探究概念的知识网络或路线图，最终对概念之间的内在联系和本质上的区别有一个深刻的理解.例如，教师可以安排学生通过图表的方式画出平行四边形、正方形、矩形和菱形的联系图，这样有助于学生更加深入、全面地掌握这些数学概念.有些概念之间有内在联系，教师要对它们做好比较，使学生对概念的本质有较深刻的认识.一般情况下，在研究一元二次方程等概念时，学生要搞清楚它们之间的联系，一旦遇到和它们有关联的问题往往就可以迎刃而解;在研究“乘方”与“幂”“方程的解”与“不等式的解”时，学生要注意分析它们之间内在的联系与区别.

对关联概念进行类比教学，既能够培养学生细致入微的观察力，又能巩固知识图谱，主动发现概念的内在联系和区别.同时，师生多进行类似的探讨，有助于学生触类旁通，掌握更多的数学知识.

（四）易混淆的概念与对比教学

在初中数学教学中，一些概念特别容易混淆，以“平方根”和“算术平方根”为例.在学习“平方根”与“算术平方根”这两个概念时，一个正数的平方根既有正数，又有负数，这两个数都是方程x2=a（a>0）的两个根，这与学生的学习思维印记是非常不一样的，此时，学生还要学习“算术平方根”的概念，很容易引起概念上的混淆，有时要取正、负两个值，有时却只能取一个正值.

对于容易混淆的概念，我们应当进行对比教学，注重这两个概念的区别和联系，并且能够从概念的内涵和外延去发现它们的相同之处和不同之处.教师指导学生画概念关系图是一种非常好的训练，通过對比，学生可以将两个概念分辨清楚.以“平方根”和“算术平方根”为例，当我们画概念图时，我们可知一个正数平方根的数量有两个且互为相反数，其中正的平方根，被称为“算术平方根”.

在初中数学的概念教学中，教师能够有针对性地选取不同的方法与策略进行教学，从而达到事半功倍的效果.教师也能够根据概念的特点和类型选取最恰当有效的方法进行教学，从而帮助学生自然地认知概念、理解概念和运用概念.

【参考文献】

[1]喻平.数学教育心理学[M].北京：北京师范大学出版社，2010.

[2]曹才翰，章建跃.中学数学教学概论（第三版）[M].北京：北京师范大学出版社，2012.

[3]吴晗，孙洪波.基于数学核心素养理念的概念教学研究：以“平方根”为例[J].数学学习与研究，2019（24），37-38.

[4]严晓冬.探究基于有效教学的初中数学概念课策略[J].数学教学通讯，2020（2）：78-80.

[5]陈永保.浅谈初中数学概念教学[J].科教导刊（中旬刊），2020（5）：132-133.

[6]宋高阳.初中数学概念教学中的问题与策略：从广东省中考方向看数学概念教学[J].中学数学研究（华南师范大学版），2020（2）：26-27.

[7]杨晓红.高中数学概念的教学策略研究[D].上海：师范大学，2011.

[8]邱祥成.理解概念理解学生理解教学：平方根概念教与学的分析[J].中学数学研究（华南师范大学版），2015（10）：22-24.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。