《一种超低旁瓣的脉冲压缩技术》-工学论文，通信论文-论文范文参考-科学狗论文网

标题

一种超低旁瓣的脉冲压缩技术

范文

张炼

[摘要]随着我国科学技术的不断发展，使得雷达系统也得到了迅速的发展。而脉冲压缩技术作为雷达技术的一项重要突破，它能够有效的增加雷达的作用距离和距离分辨率。但旁瓣作为脉冲压缩技术中的不可避免的一个问题，往往会导致雷达无法正常的进行目标的分辨。本文就超低旁瓣的脉冲压缩技术进行了深入的分析。

[关键词]超低旁瓣脉冲压缩技术

脉冲压缩技术是雷达系统技术发展过程中的一个重要技术突破。根据雷达方程，为增加雷达作用距离，需要提高雷达发射能量，对于采用发射单脉冲信号的雷达来说，意味着提升发射功率或加宽发射信号，而脉冲功率的增加受到硬件系统的限制，而仅仅增加脉冲宽度，则会导致雷达距离分辨力随之变差。脉冲压缩技术是一种能同时提高雷达的作用距离和距离分辨率的技术，具有大时宽大带宽。在发射端采用大时宽信号（通常是线性调频信号LFM），有利于提高雷达的发射平均功率；在接收端通过脉冲压缩处理将大带宽信号转为窄脉冲，达到较高的距离分辨能力。脉冲压缩技术解决了雷达的距离分辨能力和作用距离之间的矛盾，广泛应用于现代雷达，但是脉压通过匹配滤波后，在无法避免的在主瓣的两侧出现幅度低于主瓣的一系列的距离旁瓣。

旁瓣是脉冲压缩处理中最不乐见却又无法避免的问题，旁瓣是有害的，如果大目标的旁瓣较高，在信号处理时会被误认为是主瓣，从而造成虚假目标的误判；并且较强散射点（大目标）的旁瓣会压制或者掩盖临近的弱散射点（较小目标）的主瓣，导致小目标被淹没，从而引起目标漏判。因此如何降低旁瓣，提高主副瓣比，成为脉冲压缩的重点和难点。

二、脉冲压缩实现

2.1时域脉冲压缩

脉冲压缩可以通过时域卷积和频率快速傅里叶变换来实现。脉冲压缩滤波器的延迟频率特性与发射信号变化规律相反，即脉冲压缩器的相频特性与发射信号的相位是共轭匹配，这就是匹配滤波器实现脉冲压缩的原理。

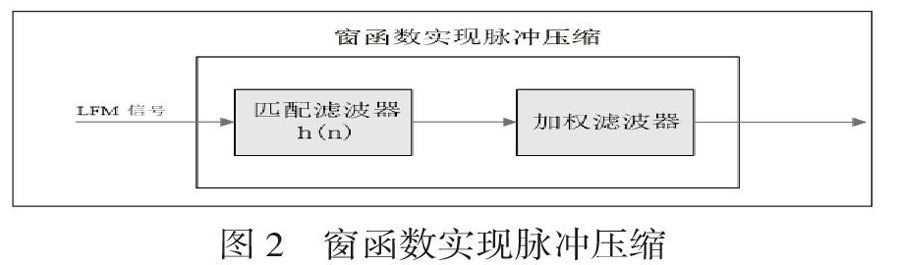
假设线性调频脉冲数字信号为s（n），则由匹配滤波器理论可知，匹配滤波器的单位脉冲响应h（n）为s（n）的镜像再共轭，即h（11）=s*（N-l-n），0

则匹配滤波器的输出信s。（n）为脉冲数字信s（n）和单位脉冲响应h（n）的卷积，即：s0（n）=s（n）*h（n）

当线性调频脉冲信号s（n）发射出去遇到目标并返回，其回波信号x（n）对应着一定的距离单元。当回波信号x（n）通过匹配滤波器（其单位脉冲响应为h（n））后会在相应的距离单元上输出信号x0（n），所以时域数字脉冲压缩处理就是将回波信号x（n）与单位脉冲响应h（n）进行时域线性卷积运算，即

x0（n）=x（n）*h（n）

由于线性调频脉冲信号为大时宽带宽积信号，其时宽T与带宽B都比较宽，而进行卷积运算的回波信号长度应该是整个处理单元的长度，并且为复信号，因此要使用高阶复数滤波器实现数字压缩处理，这在实现起来是比较麻烦的，同时通过软件处理这样的时域线性卷积效率较低。

2.2频域脉冲压缩

循环卷积可以通过离散傅里叶变换在频域完成，时域卷积对应频域相乘，所以可以在频域实现脉冲压缩。频域快速傅里叶变换法是先将输入信号进行快速傅里叶变换，接着与脉冲压缩系数相乘，然后进行逆变换，得到脉冲压缩的结果。如图1所示。FFT之前补零是为了使输入信号序列长度和滤波器的长度相同。

设回波数字信号为x（n），匹配滤波器的单位脉冲响应为h（n），根据循环卷积定理，长度为N的序列x（n）和h（n）的卷积可以通过对两个N点FFY相乘后再取IFFY来实现，即

FFT{[x（n）*h（n）N}=FFT[x（n）]×FFY[h（n）]

先对回波数字信号x（n）进行快速傅立叶变换以求得回波信号频谱，再与匹配滤波器频谱进行乘积运算，最后对乘积结果进行快速傅立叶逆变换得到脉压结果，整个过程可表示为：y（n）=IFFT{FFT[x（n）]×FFT[h（n）]）

采用频域实现脉压方法相对于时域卷积而言，其运算量将大为减少，而且如果在脉冲压缩时需要考虑加窗函数来抑制旁瓣，只需将匹配滤波器系数与窗函数在MATLAB中进行时域相乘（时域加窗）或者频域相乘（频域加窗），将其结果作为最后的匹配滤波器系数存入DSP即可，不需要增加存储器，也不会增加运算量。

需要注意的是，FFT/IFFT的点数不是任意选取的。假设输入信号的点数为N，滤波器阶数为L，那么经过滤波后输出信号的点数应为N+L-1，则所做FFY的点数必须保证大于等于N+L-1，通常取2的幂对应的数值大于等于该点数。与此对应，在对输入信号及滤波器系数进行FFT之前，要先对其进行补零处理。FFT实现比较简单，并且FPGA中已经广泛集成了FFT的IP核，所以实际工程中频域方法实现脉冲压缩非常高效且应用广泛。

2.3窗函数实现脉冲压缩

脉冲压缩通常采用加窗函数的方法来降低副瓣。窗函数实现脉冲压缩就是在脉冲压缩滤波器后面级联一个具有某种锥削函数频率响应的副瓣抑制滤波器，称这种锥削函数为加窗函数，常用的加窗函数有海明窗、凯撒窗和布莱克曼窗等。如图2所示。

时域实现窗函数的脉冲压缩方式分两步进行：

第一步：将脉冲压缩滤波器h（n）和加窗函数w（n）进行卷积，获得加窗函数后的滤波器的响应hw（n），则

hw（n）=h（n）*w（n）

第二步：将回波信号x（n）与匹配滤波和窗函数卷积后的脉冲响应hw（n）进行时域线性卷积运算，得到降低旁瓣的脉冲压缩结果，即：x0（n）=x（n）*hw（n）

频域实现脉冲压缩滤波器的频率响应为原脉冲压缩滤波器频率响应与副瓣抑制滤波器频率响应（即频域加窗函数）的乘积，即：Hw（k）=H（k）w（k）=FFT[h（n）]×FFT[w（n）]

然后将回波信号频谱FFT[x（n）]与加窗函数的脉冲压缩滤波器的频谱Hw（k）进行乘积运算，对乘积结果进行快速傅立叶逆变换得到脉压结果，即：y（n）=IFFT{FFT[x（n）]×Hw（k）}

通过加窗函数进行加权处理可以降低旁瓣，然而不可避免会对主瓣展宽，牺牲一定的距离分辨和性噪比，加不同的窗函数加权对脉冲压缩有不同的影响，需要进行比对选择最优的窗函数。不加窗函数和加不同的窗函数的脉压结果如图3所示，蓝色为不加窗，红色为加了海明窗，黑色为加了凯撒窗（）。

可以看出不加窗时，主副瓣比约17dB，加了窗函数后，主瓣展宽但副瓣大幅度压缩，主副瓣比明显增加，达到50dB以上，且不同的窗函数主瓣展宽程度和旁瓣的压缩程度不同，过渡带和第一旁瓣的位置也不同。虽然加窗函数加权可以明显降低副瓣，提高主副瓣比，但同时也不可避免带来了信噪比损失和主瓣展宽的问题，信噪比损失会降低雷达作用距离，而主瓣展宽则会降低雷达探测距离的分辨能力。

为了减少匹配滤波后旁瓣对系统性能的影响，需要获得最优的幅频特性函数，在对造成干扰的旁瓣信号进行最大抑制的同时，最小限度地影响到距离分辨力和信号检测能力。为此，本文提出一种超低旁瓣的脉冲压缩方法，通过加双凯撒窗的方式进行加权，达到整体性能最优。

三、加双凯撒窗实现脉冲压缩

3.1原理

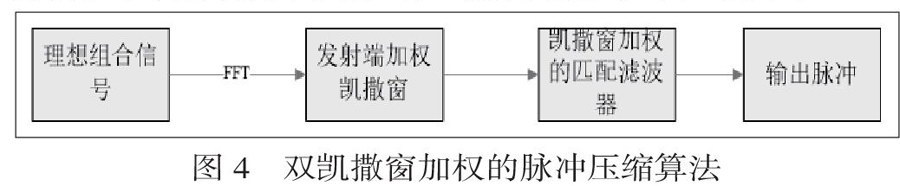
加双凯撒窗是在发射机和接收机中同时用用凯撒窗进行加权，发射信号经过加窗处理后不再具有原LFM的频谱特点，边缘的阶跃性大大减小，菲涅尔纹波也减小，从而有效降低旁瓣。双凯撒窗加权的脉冲压缩算法流程如图4所示。

设发射信号为s（t），发射端和接收端的时域加权函数都是w（t），h（t）是针对s（t）设计的理想匹配滤波器冲激响应函数，则经过发射端和接收端加权处理后得到的脉冲压缩输出信号为：y（t）=[s（t）×w（t）]*[h（t）×w（t）]

实际工程应用中，发射信号需要通过功放放大后输出，而功放的工作点在很多情况下工作设在饱和区或接近饱和区，因此，加凯撒窗后发射信号将会出现严重的幅度失真。为解决此问题进行改进，在加权过程中，在发射端就不用进行窗函数加权，发射信号仍为LFM信号，只在接收端等效加权hw（t），时域实现时，将脉冲压缩信号输出等价为：

y（t）=s（t）*hw（t）

通过频域实现的方法计算窗函数的等价函数hw（n）：

hw（n）=IFFT{FFT[s（n）×w（n）]×FFT[h（n）×w（n）]/FFT[s（n）]}

通过hw（n）得到滤波器的频率响应，具体实现时，按照图1进行，只是将脉冲压缩系数更换为hw（n）。

3.2仿真分析

加双窗函数与不加窗函数的比较与加单窗函数类似，加双窗时，不同的窗函数对脉冲压缩有不同的影响。与不加窗比较，加双窗函数时主副瓣比更大幅度增加，达到了70dB以上，双凯撒窗甚至达到了80dB以上，加双凯撒窗与双海明窗比较，脉宽展宽幅度小，且过渡带宽更窄，副瓣更加大幅度压缩。下面比较加单窗函数和加双窗函数的结果，在脉冲展宽和主副瓣比之间寻找最优性能。加不同的单窗函数和加不同的双窗函数对脉冲压缩有不同的影响。与加单窗比较，加双窗时主瓣展宽幅度很小，几乎没有展宽，但主副瓣比继续明显增加，增加20dB以上，加双凯撒窗与双海明窗比较，双凯撒窗展宽幅度更小，近距的旁瓣明显降低，过渡带宽更窄，副瓣更加大幅度压缩。加双凯撒窗，对整体的性能是最好。

结论：本文通过理论分析和仿真对比，探讨了双凯撒窗加权算法在旁瓣抑制中的应用及其优越性。与不加窗比较，加单窗函数的主旁瓣比增加50dB以上，虽然主旁瓣比得到了一定的提高，但是主瓣展宽，牺牲了距离分辨力和信噪比SNR；与加单窗比较，加双窗的主瓣展宽幅度很小，几乎没有展宽，主副瓣比得到了明显的提升，进一步提升约20dB，且加双凯撒窗的主瓣展宽曲线更加陡峭狭窄，主瓣宽度的增加幅度也较小，近距的旁瓣明显降低，过渡带宽更窄，副瓣更加大幅度压缩，主副瓣比达到80dB以上，一种非常有效的得到超低旁瓣的脉冲压缩方法。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。