《浅析培养学生一题多解的思维能力》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

浅析培养学生一题多解的思维能力

范文

胡春阳

摘要：数学教学的主要目的是为了培养学生思维能力，让学生可以举一反三，理解数学知识内涵，并且应用数学知识解决各类问题。在初中数学教学中，动态四边形问题是检验、锻炼学生思维能力的重要题型之一，基于此，本文立对培养学生一题多解的思维能力进行研究，希望以下内容的论述可以具有一定参考价值。

关键词：动点;动态四边形;平行四边形;一题多解

中图分类号：G4? 文献标识码：A? 文章编号：（2020）-27-056

引言

就目前学生解题情况而言，一题多解的思维能力培养一直是难点之一，因此，需要通过归纳解题思路与教学方法保证学生可以顺利解题。

一、几何证明下的一题多解教学

例1如图，在五角星ABCDE中，∠A，∠B，∠C，∠D，∠E的和等于多少度？请加以证明.

[教学预设]

方法1：如图，根据三角形外角的性质得到∠1=∠C+∠E，∠2=∠B+∠D，将求五个角的和转化为求一个三角形的内角和.

方法2：如图，连接CD，利用“八字形'得到∠B+∠E=∠1+∠2，依然将求五个角的和转化为求一个三角形的内角和.

方法3：如图4找到燕尾模型”，得到∠1=∠A+∠C+∠D，再根据∠1与∠2互为对顶角得到∠1=∠2，从而知道这五个角的和为180°.

在利用法3解决这个问题时要先证明燕尾模型"中四个角的关系，同样可以得出多种方法.

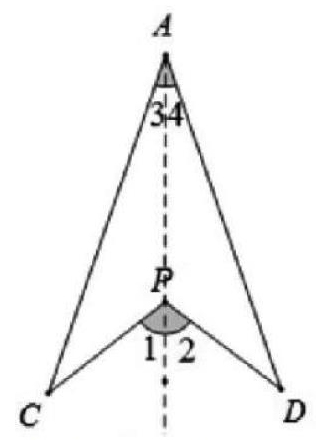
方法1：如图，连接CD，根据三角形内角和为180°.得到∠P=180°-∠1-∠2，∠A+∠3+∠4=180-∠1-∠2等量代换得到∠P=∠A+∠3+∠4.

方法2：如图6，连接AP，根据三角形内角和为180°得到∠1=180°-∠C-∠CAP，∠2=180°-∠D-∠DAP，所以∠CPD=360°-∠1-∠2=∠C+∠CAP+∠D+∠DAP=∠C+∠CAD+∠D.

方法3：如图7，连接AP并延长，因为∠1、∠2分别是△ACP、△ADP的外角，所以∠1=∠3+∠C，∠2=∠4+∠D，所以∠CPD=∠1+∠2=∠3+∠C+∠4+∠D=∠CAD+∠C+∠D.

二、一题多解具体教学方法

2.1将“一题多解”应用于教学情境设计

初中数学教师在开展教学情境设计：工作的过程中，可以着手于设计问题的悬疑性，通过创设生活中普遍存在的情境，引导学生进入至探究性问题现象中，将旧知识内容完美过度至新知识内容。在初中数学教学活动中，教师利用情境设计，能够确保所设计探究性问题的科学性与合理性，对学生产生一定的吸引力，调动起学生的探究兴趣。在利用“一题多解”时，初中数学教师应当以教学大纲要求为基础，高度重视学生的整体发展，对系统、灵活的教学情境开展设计工作，透过相关教学情境，帮助学生通过自身经验，将新知识与旧知识结合的关键点挖掘出来。利用新旧知识的摩擦与碰撞，充分调动起学生的求知欲望，使学生感知到高中数学的魅力，为以后的数学学习活动，创造良好条件。

2.2将“一题多解”应用于例题讲解

在初中数学教材的各节课后，均设置了相应的例题，这些例题难度系数比较低，主要为了帮助学生高效巩固有关教学内容。利用这些所设计的例题，能够帮助学生深入理解相关知识内容，强化学生记忆，能够将丰富多样的例题素材提供给教师。在对这些例题进行运用的过程中，大多数情况下，教师运用的是变换习题形式，帮助学生通过其他视角，开展有关教学内容的学习与理解活动。利用“一题多解”，开展例题教学活动，能够促使学生通过解题思路，深入理解教学内容，实现教学质量与学习效率的提升，促进学生思维能力培养与提升活动的开展。比如，在进行‘等差数列的前n项和”这一内容教学时候，关于例题中的已知条件，学生可以通过所掌握的知识体系作出解答，并与例题中解题思路的差异，开展相关对比活动。在此前提条件下，教师立足于教学目标，充分发挥出自身的引导作用，帮助学生依据例题中的阶梯思路的提示内容，对其他解题方式方法进行查找，这样能够实现学生解题思路的拓展，增强学生学习能力的培养。

2.3将“一题多解”应用于公式推导

在高中数学的众多教学内容中，公式这一教学内容居于重要地位。学生在对数学习题进行解答的过程中，至关重要的条件之一就是公式。在解答高中数学习题的过程中，公式所占据的比重比较大。所以，学生应当在教师的指导活动下，确保公式掌握与运用的灵活性。而不是利用死记硬背形式，对其开展机械化记忆活动。在开展高中数学教学工作的過程中，关于公式的推导教学过程方面，教师应当给予高度关注，不断提升学生对公式的理解能力与应用能力。公式推导也属于解题过程的范畴，能够帮助学生了解公式应用技巧。在推导公式的过程中，应用“一题多解”，能够对学生思维进行培养，确保学生灵活运用公式这一教学目标的完成。比如，关于等差数列通项公式方面，可以将“一题多解”的方法引入进来，第一，可以依据a2=a1+d，a3=a2+d=a1+2d...的形式，开展相关推导活动，得出相关公式。第二，可以着手于等差数列，利用累计相加形式，获取差数列公式，在推导数列通项公式的过程中，累加法的运用次数非常多，这样能够帮助学生强化公式的学习，还能够使学生了解多种不同的解题方式方法，实现学生思维的高效拓展，为学生数学思维的发展与进步做出贡献。

结论

综上所述，对于学生而言，解决这类问题首先需要基础知识扎实，这样才能在综合类试题中抽丝剥茧，还需要立足于图形，完成图形的解析，从而思考一题多解最终的落脚点，以静制动解决问题。

参考文献

[1]裴润济.初中数学复习方法的探究[C].中华教育理论与实践科研论文成果选编（第2卷）.中国教育教学丛书编委会，2010：808一810.

[2]程华.数学课堂合作学习问题透析——以西安市某初中为例[J].教育导刊，2010（01）：40一42.

[3]俞凯.精彩来自不断的争鸣与探索——在实验几何中培养学生探究能力的一次教学尝试[J].中学数学教学参考，2008（14）：21一23.

[4]孟凡慧.数学习题教学与学生思维能力培养方法谈[J].科技信息（科学教研），2007（35）：172.

[5]孟庆锋，孟庆宇.浅谈创新精神在初中数学教学中的体现[J].黑龙江教育（中学版），2003（Z2）：72一73.

[6]汪健.从“一题多果”看中考对初中学生数学能力的新要求[J].数学教学通讯，1995（04）：24一25.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。