《相悖答案的产生与电势能概念的深层分析》-理学论文，中学数理化论文-论文范文参考-科学狗论文网

标题

相悖答案的产生与电势能概念的深层分析

范文

谭东敏孔令峰张井卫

[摘? ?要]高中物理教学中，有时会发现：一个问题从不同角度分析解答，会得出不同的结论，两种分析解答过程似乎都有道理，是否真的如此呢？文章以两道点电荷在电容器中的电势能的变化问题为例进行分析探讨。

[关键词]点电荷;电容器;电势能

[中图分类号]? ? G633.7? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2021）17-0039-04

一线教师在日常的备课、教学、解题及教学反馈等过程中，时常会发现各种各样的问题。有的问题，真的值得我们一线教师深入探讨。本文通过对两道点电荷在平行板电容器中电势能变化问题的分析解答，发现得到两个相悖的结论，并以此为出发点探讨产生相悖结论的原因，并在此基础上对电势能概念作深层次的分析探讨。

一、相悖答案产生与思考

高二上学期的一次月考后，一位实习老师跟我们讨论这次月考物理试卷上的一道关于电容器的试题（题目1）。

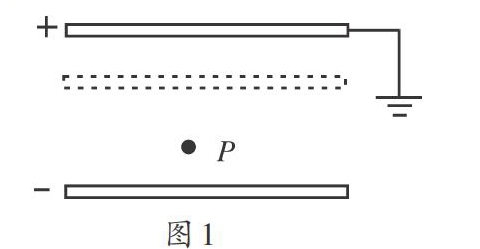
题目1.一平行板电容器充电后与电源断开，正极板接地，在两极间有一正电荷固定在P点，如图1所示，以U表示两极板间的电压，E表示两极板之间的场强，Ep表示该正电荷在P点的电势能，若保持负极板不动，而将正极板移至图中虚线所示位置，仍保持正极板接地，则（）。

A.[U]变小，[Ep]变大 B.[U]变小，[Ep]不变

C.[U]变大，[E]不变 ? D.[U]变大，[E]变大

解析：平行板电容器充电后与电源断开，因此电容器的电荷量不变，将正极板移到图中虚线所示的位置时，板间距离d减小，根据[C=εS4πkd]可知，电容器的电容C增大，Q一定，根据[U=QC]可知板间电压U变小;根据[E=Ud]，[Q=CU]，[C=εS4πkd]，联立可得[E=4πkQεS]，可知E与d无关，E不变;P与正极板间的距离减小，上极板与P点的电势差由公式[U=Ed]可知，P与正极板之间的电势差减小，且[U=0-φp]，则P点的电势变大，正电荷在P点的电势能[Ep]变大，故A正确，BCD错误，故选A。

关于电势能[Ep]的变化，上述解释是从[P]点的电势变化着手，分析得出P点的电势变大，那么在[P]点的正电荷的电势能变大。

这位实习老师认为，正点电荷固定不动，即点电荷没有发生位移，那么电场力对其就没有做功，根据“功是能量变化的量度”来分析，点电荷的电势能不可能变化。而且这位实习老师还对比了2016年天津高考理综试卷物理部分的第4题（题目2）。

题目2.如图2所示，平行板电容器带有等量异种电荷，与静电计相连，静电计金属外壳和电容器下极板都接地，在两极板间有一固定在[P]点的点电荷，以[E]表示两板间的电场强度，[Ep]表示点电荷在[P]点的电势能，[θ]表示静电计指针的偏角。若保持下极板不动，将上极板向下移動一小段距离至图中虚线位置，则（）。

A. [θ]增大，[E]增大 B. [θ]增大，[Ep]不变

C. [θ]减小，[Ep]增大D. [θ]减小，[E]不变

解析：若保持下极板不动，将上极板向下移动一小段距离，则根据[C=εS4πkd]可知，C变大，Q一定，则根据[Q=CU]可知，U减小，故静电计指针偏角[θ]减小;根据[E=Ud]，[Q=CU]，[C=εS4πkd]，联立可得[E=4πkQεS]，可知Q一定时，E不变;根据[U1=Ed1]可知P点离下极板的距离不变，E不变，则P点与下极板的电势差不变，P点的电势不变，则[EP]不变;故选项ABC错误，D正确。

相悖答案的发现题目2中，点电荷同样没有移动，该题的解析同样是从点电荷相对接地极板的电势角度切入，解释其电势能不变。该实习老师是从电场力做功的角度分析电荷电势能变化的：点电荷固定，电场力对该点电荷不做功，故电势能不变化。从这两个角度分析得到的结论相同，从电场力做功的角度解释更为简洁。

但是我校的这道月考题，如果按照参考答案，从电荷所处的电势变化来分析，得到电荷的电势能增大的结论;但是从电场力做功改变电势能的角度来分析，电势能则是不变的。众所周知，一个正确的结论从不同角度分析都应该是自洽的，从不同维度分析同一个问题得到的结论应该也是相同的。出现不同的结论，问题在哪里呢？

二、从电势能的概念探讨“答案相悖”的原因

人教版教材中《电势能和电势》这节课的教学中常用类比重力势能的方式引入电势能的概念——“由于移动电荷时静电力做的功与路径无关，电荷在电场中也具有势能，这种势能叫作电势能，可用[Ep]表示”，“电荷在某点的电势能，等于把它从这点移到零势能位置时静电力做的功”;又从定义“电势”[φ=Epq]的式子可演变出电势能的表达式[Ep=qφ]。关于电势能的变化，教材中的表述是：“功是能量变化的量度，静电力做功等于电势能的减少量”。如果对教材内容的解读不够，人们就会产生这样偏颇的观点：从“表面”上看，电势能好像是电荷的，认为其电势能的变化应由该电荷所受静电力做的功决定。

其实这位实习老师在这个问题的处理上忽略了两点。

第一，电势能的系统性。不管是重力势能，还是电势能，都是系统共同具有的，而不是物体或点电荷单独具有的，但是我们为了表达简要起见，往往说成“物体的重力势能”或“电荷的电势能”，在这样的习惯性交流表达的大环境中，容易使人忽视势能的系统性，所以作为教师，对势能的理解一定要时刻铭记它的“系统性”。既然势能具有系统性，那么势能就不是由单个物体或单个点电荷决定的，而是由组成系统的各方共同决定。势能是否变化也不能只看保守力对所谓的单个物体或单个点电荷做功的情况，而是从彼此之间的相互作用力对彼此各方的做功情况来分析。

在题目1中，由于接地的上极板带正电与P点的正电荷相互排斥，上极板向下移动是靠近P点的正电荷，点电荷P虽然固定不动，但它们之间的相互作用力对上极板做负功，故点电荷与上极板之间的电势能增加。这里我们只是讨论点电荷与电容器之间的电势能，撇开了电容器自身系统的静电能。

第二，忽略了电势能的相对性。重力势能和电势能的多少都是相对零势能位置而言的。题目1中上极板接地，一般我们习惯认为，上极板电势为零。虽然在平移上极板的过程中，电场力对P点的电荷没有做功，但是这个过程中极板间的电场强度没有变化，P点与上极板的距离d发生了变化，那么P点与上极板的电势差[U=Ed]一定发生变化，所以P点的电势也就变化了，电势能自然也要变化了。从“系统性”分析和从“相对性”分析都得到相同的结论：电势能是增加的。所以，我们在解决问题的时候不妨尝试从不同角度切入，尝试用多种方法解决，在多种思路的交织中，我们会构建更全面、更系统的思维关联，对我们解决新的问题不断提供启发性思考。还有可能挖掘出新的问题，对这些新问题的思考、研究，会使我们对这类问题有更深层次的理解。

该实习老师在解题过程中发现的问题是关于物理概念的，物理概念是客观事实的共同属性和本质特征在人脑中的准确反映，是人们在长期认知客观事物和自然现象的过程中，经过观察、思考、猜想、建模、实验验证、分析比较、归纳总结等环节而得到的抽象化表征。在中学物理概念教学过程中，学生或教师对物理概念认识和理解上难免会出现一些偏差，对概念的广度和深度认知不够、不透。但对一个物理概念全面、精准的认知，对物理教师而言至关重要，我们决不能将自己偏颇的认识甚至错误的概念传授给学生，这也是教师上课前要充分备课的重要原因。

三、解决“答案相悖”问题的过程中发现新问题

如果从系统电场力（相互作用力）做功的角度看，题目2中的电势能也应该是变化的。与上述解析结论是不统一的。上极板与固定在P点的点电荷无论是同种电荷还是异种电荷，两者间距发生变化时，虽然电场力对P点的电荷没有做功，但是电场力对上极板的电荷一定做功，那么，P点的电荷与极板之间的电势能应该发生变化，但是题目2的解析中结论是不变的，该问题不由使我们产生疑虑。关于这个疑虑的新问题，曾向同事请教。

同事认为，点电荷在电场中拥有的电势能的多少以及变化情况，都应该以零势面为参考，题目2中参考答案的解析是没有问题的。至于做功问题，不应该以上极板——非零势极板，来讨论电势能的变化，因为电势能是相对于零势面而言的。关于点电荷与电场之间的电势能的变化不能“片面”地以单个极板与点电荷之间的相互作用力做功来讨论，电容器之间的电场是两极板共同形成的，那么，电荷在电容器电场中的电势能是将两极板共同“贡献”糅合到以零势面为参考的条件之中的。

该同事还以我们熟悉的重力势能为例，类比解释这个问题。如图3所示，质量为m的小球相对零势面的重力势能[Ep=mgh]，不会以上面的非参考平面a的（上）下移动而改变的，因为小球相对零势面b做功的“能力”没有改变。同理，点电荷的电势能也是相对零势面而言的，题目2中平移电容器的上极板并不会影响电荷相对下极板（零势面）的做功“能力”，故电荷的电势能是不变化的。

该同事很好地用高中教材的相关知识进行解释，但是依然没能解决“系统之间的静电力（保守力）做了功，与系统的电势能却不变”之间的矛盾。那么，问题在哪里呢？一天放学后，我们针对图3进行深入探讨，探讨中发现电荷与电容器之间的电势能和重力势能存在一点不同：在地球表面重力场是地球单侧形成的，而电容器极板间的电场是两极板共同激发的。从这个“不同点”切入，找到了这个新问题的根源。

四、平行板电容器电势能的理论分析

首先，我们要了解接地电容器的两极板的电荷分布情况，从而确定电容器的电场情况，进而清晰地分析点电荷在电容器两极板间的电势能。通过查阅与电容器相关的资料，找到了相关的内容。由于极板接地，两极板外侧表面均无电荷，电容器两极板面积相对两极板的间距而言非常大（如图4）。若忽略边缘效应，两极板内侧表面均匀分布等量异种电荷，在极板间共同形成匀强电场。根据对称性，两极板的电荷在极板间激發的电场相同，合场强为单极板激发电场强度的两倍[2]。

根据高斯定理，单个极板激发的电场强度[3]： [E+=E-=σ2ε0]? ? ? ? ?①

根据电场叠加，带电电容器之间的电场强度： [E=E++E-=σε0]? ? ? ? ?②

点电荷靠近或远离带电极板[Δd]与带电极板靠近或远离点电荷[Δd]的过程中，其电势能的改变效果是等价的，根据电势能变化与静电力做功之间的关系，不难理解，

电势能均变化：[ΔEp=-W电=-qσ2ε0?Δd]③

①②③式中[σ]为极板电荷面密度，[ε0]为介电常数，q为点电荷的电量，[Δd]是点电荷与极板间距的变化量。

题目1中，因为下极板没有上下移动，所以点电荷与下极板之间的电势能没有变化，那么，点电荷与电容器之间的电势能的变化只能来源于上极板向下移动而引起的“贡献”。如果，上极板向下平移[Δd]，那么电量为q的正电荷与电容器的电势能的增加量就是[ΔEp=qσ2ε0?Δd]。

如果按照题目1参考答案的解题思路去计算电势能的变化，我们便会发现问题的端倪。若上极板向下平移[Δd]，由于极板间的电场强度[σε0]不变，则点电荷所处位置与上极板之间电势差的变化量则为[ΔU=σε0?Δd]。因为上极板接地，我们认为其电势为0，所以，点电荷所处位置P点的电势变化量为[Δφ=σε0?Δd]，因此点电荷与极板间的电势能变化了[ΔEp=qσΔdε0]，与此过程中电场力做功不符，且为静电力做功的两倍。同样，根据电势能变化与静电力做功之间的关系，题目2中上极板移动[Δd]距离，P点的电势能也应该变化[qσ2ε0?Δd]，但是按上述解析的思路分析，点电荷在P点的电势能是不变的。这样的结果真耐人寻味。

我们认为，对孤立带等量异种电荷的电容器来说，板间电场的零电势面不应为接地极板，应与两个孤立的等量异种点电荷的电场一样，是与等量异种电荷（极板）等距的中央平面。

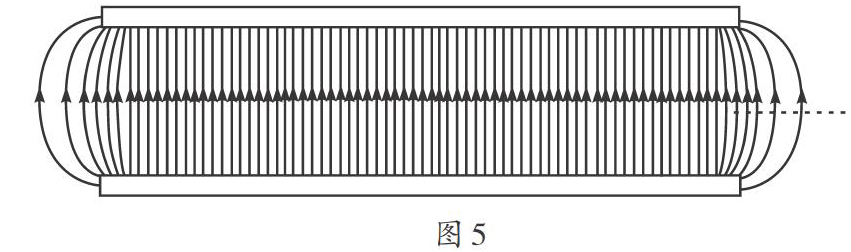
由于均匀带电平面的电势：[φ=-σ2ε0x]，[x]是到带电平面的距离[4，5]。那么，带等量异种电荷的两极板的电荷面密度相同，均为[σ]。如果极板间距为d，设到正极板距离为x处电势为零，则满足：[-σ2ε0x+--σ2ε0（d-x）=0]，可知，[x=d2]。也就是说，带等量异种电荷的极板共同激发的电场的零势面为极板间的中央平面（如图5）。电容器的极板相对它们的间距是很大的，但是一个平行板电容器相对可视的空间而言，则显得非常小，那么带电的电容器可看作有限区域内的点电荷系，无穷远是零势点的最佳优选点[4]。

以电容器极板间的中央平面为零势面，题目1、题目2的矛盾也就迎刃而解了。题目1中，当上极板向下平移[Δd]，则中央平面（零势面）会向下移动[Δd2]，那么，P点到零势面的电势差减少了[ΔU=EΔd2=σ2ε0Δd]，显然，P点电势就增加了[Δφ=σ2ε0Δd]，那么，正电荷与电容器之间的电势能增加了[ΔEP=qσ2ε0Δd]，这个结果与静电力做功完全相符。

题目2的情景中，电荷与电容器之间的电势能变化量与静电力做功依然完全相符，这里不再赘述，读者可以自行推导验证。

关于电荷与电容器之间的电势能是高中课程中回避的一个问题，却是一个值得我们探讨的问题，从诸如题目2的高考真题中，我们可以看出，高考真题可能有意无意地避开了它，但面对这样的问题，我们教师可以深入地思考探究。

[? ?参? ?考? ?文? ?獻? ?]

[1]? 张维善.人教版课程标准实验教科书《物理》选修3-1[M].北京：人民教育出版社，2017.

[2]? 缪钟英.中学物理教师进修用书《电磁学问题讨论》[M].合肥：中国科学技术大学出版社，2019：8.

[3]? 梁灿彬.大学普通物理学教程《电磁学》[M].北京：高等教育出版社，2018.

[4]? 金仲辉，陈秉乾 .静电场电位零点的选择[J].大学物理，1984（8）：44-45.

[5]? 封小超.关于零电位选择的几个问题[J].大学物理，1986（7）：13-16.

（责任编辑易志毅）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。