网站首页  词典首页

请输入您要查询的论文：

　

标题 粗粒土与结构接触面往返剪切试验的PFC2D数值模拟
范文 赵亦凡　刘文白






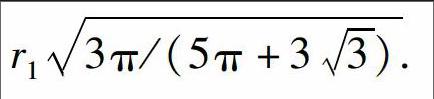
摘要：为研究土颗粒的细观，利用PFC2D对粗粒土与结构接触面往返剪切试验进行数值模拟，研究接触面的剪胀特性与颗粒平移、旋转、破碎的关系及体应变可逆性和不可逆性规律.当不考虑颗粒破碎时，土体具有可逆性剪胀体应变；当考虑颗粒破碎时，土体具有不可逆性剪胀体应变.验证接触面体应变是由一个可逆性体应变分量与一个不可逆性体应变分量构成的.PFC2D位移场试验及类长形颗粒定向试验表明可逆性体应变主要由颗粒平移和颗粒自身旋转产生.对考虑颗粒破碎现象的黏结模型分析表明，不可逆性体应变主要由压密和破碎两种物态演化现象产生，颗粒破碎起主要作用.
关键词：接触面； 往返剪切； 可逆性剪胀； 不可逆性剪胀； PFC2D
中图分类号： P642.116
文献标志码： A
Abstract：In order to study the microscale of soil particles， the cyclic shear test of the gravalstructure interface is simulated by PFC2D. The relationships between the dilatancy of the interface and the particle translation， rotation， breakage， and the rules of reversible and irreversible volume strain are studied. The soil has the volume strain of reversible dilatancy without considering particle breakage and the soil has the volume strain of irreversible dilatancy with considering particle breakage， which verifies that the volume strain of the interface is composed of a reversible volume strain component and an irreversible volume strain component. The PFC2D displacement field test and the elongated particle orientation test indicate that the reversible volume strain is mainly produced by particle translation and rotation. The analysis on the binding model considering particle breakage shows that the irreversible volume strain is mainly produced by the evolution from particle compaction to particle breakage， where the particle breakage plays a main role.
Key words：interface； cyclic shear； reversible dilatancy； irreversible dilatancy； PFC2D
0引言
土是散粒状介质组成的颗粒集合体，而土颗粒的细观组构变化是土宏观形变的内因[14]，所以对土颗粒的细观研究是有必要的.以往学者[57]根据土与结构接触面的宏观物理试验，归纳出土与结构接触面的强度率、剪切率、剪胀率、压缩率和演化率等5条基本规律.本文基于前人对粗粒土与结构接触面剪胀率的研究，进一步进行接触面剪胀率的细观研究.随着计算机数值计算的不断发展，以CUNDALL等1979年提出的颗粒离散元为代表的数值分析法成为土力学的一个主要研究手段.颗粒流程序（Partical Flow Code，PFC）作为离散元的一种，能较好地模拟土的性状.国内学者已用PFC对土的细观机理进行研究：周健等[8]用PFC模拟砂土剪切带的形成；刘文白等[9]用PFC进行上拔荷载作用下扩展基础的细观数值模拟.
对土力学试验的数值模拟是PFC的一个重要运用，对直剪、单剪和双轴的试验已取得成果.[1012]本文基于土与结构接触面的往返剪切试验[12]，运用PFC2D进行数值模拟，研究接触面的剪胀特性，剪胀体应变的划分，可逆性体应变和不可逆性体应变的产生机理和基本规律，土颗粒的位移规律、旋转规律和破碎现象.
1PFC2D数值模拟模型的建立
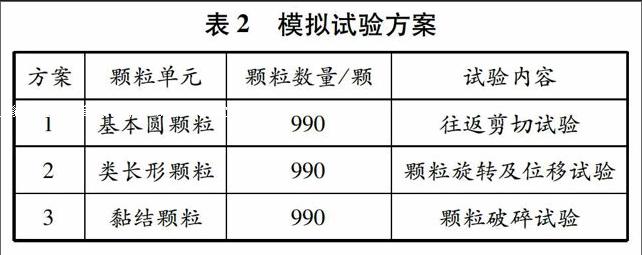
用PFC2D中的Wall命令定义4面墙体，分别模拟结构物和加荷板，见图1.在往返剪切试验过程中：上底板及左右墙通过伺服控制施加恒定的竖向压力及围压，控制下底板（有一定的粗糙度）以一定速率左右来回运动，以实现宏观上的往返剪切；土体模拟试样宽为100 mm，高为100 mm，其高宽比与物理试样相同；土颗粒最大半径为2 mm，最小半径为1 mm，初始孔隙率为0.3；采用半径扩大法，放大系数为1.6，通过半径放大法固结粗粒土试样；土体密度为2 500 kg/m3，颗粒半径随机均匀分布，共计990颗土颗粒.
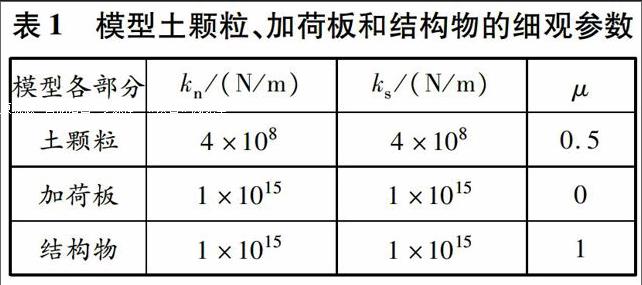
PFC2D提供的接触刚度模型有线性接触模型和HM非线性接触模型.本文采用线性接触模型就能满足要求，模型的细观参数有法向接触刚度kn，切向接触刚度ks和颗粒摩擦因数μ.经过模型试验的反复调试，最终选定墙体的kn=ks=1×1015 N/m，μ=0.5.土颗粒、加荷板和结构物的细观参数见表1.
2颗粒模型的建立
2.1基本圆颗粒
基本圆颗粒通过PFC2D中ball命令生成，半径r1取值为1～2 mm.在不考虑颗粒破碎的情形下，粗粒土与结构接触面往返剪切试验采用基本圆颗粒，见图2a.
2.2类长形颗粒
为更直观地观察并记录试验中颗粒的旋转，可用PFC2D中CLUMP命令建立类长形颗粒，根据类长形颗粒长轴的始末位置统计颗粒旋转量.采用等面积法在原颗粒处生成由3个相连小圆颗粒组合成的类长形颗粒（见图2b），该类长形颗粒可视为一个独立的大颗粒，不会分裂成小颗粒.类长形颗粒生成时长轴方向随机分布，新生成的颗粒半径r2=r13π/（5π+33）.
2.3黏结颗粒
在考虑颗粒破碎情形下，建立接触黏结颗粒，再进行粗粒土与结构接触面往返剪切试验.黏结颗粒（见图2c）由3个小圆颗粒和2个黏结键组成，同样采用等面积法生成，颗粒半径也取为r2.通过设置黏结强度控制土颗粒的破碎：取法向黏结强度和切向黏结强度都为20 kPa，当黏结颗粒所受外力超过黏结强度时，黏结键发生断裂，颗粒破碎成3个小颗粒，否则不发生破碎.发生破碎的黏结颗粒越多，表明颗粒破碎程度越严重.
3剪胀率及体应变的划分
土作为离散介质的集合体受到结构物的约束，在结构接触面处发生既不同于土、又不同于结构材料的力学响应，涉及大变形、非线性、局部不连续等力学问题.文献[8]通过PFC2D模拟粗粒土与结构
接触面的往返剪切试验，研究接触面处的剪胀率，证实剪胀率中剪胀体应变v由可逆性体应变分量vd，re和不可逆性体应变分量vd，ir构成（v=vd，re+vd，ir），并依此分析可逆性体应变的基本规律和不可逆性体应变的基本规律.
在常法向应力σ和围压均为400 kPa的情况下，下底板以6×10-4 mm的步幅左右来回剪切（见图1），共进行10个循环.图3为PFC2D模拟的往返剪切作用下结构接触面处土的剪应力τ随循环次数N变化的曲线.
分析图3可知：
（1）接触面处土的剪应力（平均剪应力=施加的剪力/上底板宽度）随剪切位移的增大而增大；
（2）剪应力出现峰值后不再随剪切位移的增大而增大，且在剪应力达到峰值时接触面处土颗粒剪切强度达到极限状态；
（3）在剪切位移转向时，剪应力相应从峰值下降，并随剪切位移的增加达到反向剪应力峰值；
（4）每个剪切循环内，剪应力变化具有规律性，即具有相同剪应力峰值及相同的变化曲线.
4剪胀体应变的可逆性体应变
4.1可逆性体应变的基本规律
通过PFC2D自带的FISH语言，监测每一时步试样的体应变（在PFC2D中，以每一时步试样总面积（即四面墙体所围面积）变化表示试样的体应变）.根据体应变是否随循环剪切次数增长而单调变化定义可逆性体应变和不可逆性体应变.将体应变曲线上下波动的那部分定义为可逆性体应变，体应变曲线中移除上下波动后剩余的部分定义为不可逆性体应变（不可逆性体应变呈抛物线向下），见图4.
图4为不考虑颗粒破碎时，10次往返剪切内可逆剪切体应变随剪切循环次数变化的情况.由于剪切位移是从结构物中间开始的，单次数剪切比双次数剪切的体应变峰值多半个循环的剪切体应变，造成图中单次数循环体应变峰值总比双次数循环体应变峰值多半个循环的剪切体应变.
由图4可知：
（1）在一个完整的来回剪切循环内，可逆性体应变从0增大至峰值，又完全回到0.
（2）由于土颗粒试样同时受到围压和剪切作用，试样体应变的增加和减小可分别定义为试样的体胀和体缩.可逆剪切体应变随相应剪应力变化而同时变化.当剪切作用方向与初次剪切作用方向相同时，可逆性体应变表现为体缩；而当剪切方向与初次剪切方向相反时，可逆性体应变表现为体胀.
（3）由于围压作用不会使试样产生可逆性体应变，而剪切作用下由于颗粒的平移和颗粒自身的旋转，试样既能产生体缩现象又能产生体胀现象，所以这部分可逆性体应变主要是由结构接触面处土颗粒的平移和自身旋转产生的.
4.2颗粒的平移
为研究粗粒土与结构接触面在往返剪切试验下颗粒的可逆性体应变，采用基本圆颗粒进行位移场试验.图5显示在一个完整往返剪切作用下的土颗粒的平移变化.当施加初始方向向左的剪切力（图5b）时，土颗粒会围绕试样中心偏右的一个“旋转中心”向左位移，颗粒与颗粒的平移是连续变化的，且靠近结构面处的颗粒位移值最大.当施加初始方向向右的剪切力（图5c）时，形成新的结构面异向性，颗粒随着剪切位移的增加也逐渐向右位移，此时会在试样中心产生偏左的一个“旋转中心”.
4.3颗粒旋转
利用类长形颗粒观察往返剪切试验中颗粒的旋转.通过颗粒定向程序统计一个完整剪切循环后全部颗粒自身的旋转分布，见图6.由图6可以观察到几乎所有颗粒都发生旋转（0°不存在），且初始剪切方向向左与向右两种情况下颗粒旋转角度分布相差不大.剪切前颗粒长轴方向随机分布，剪切时颗粒在总体上呈定向排列.通过模拟试验可知，在结构接触面处的颗粒旋转角度较大，原因可能是：颗粒旋转是受到结构物剪切作用产生的，因此靠近结构接触面的颗粒先发生旋转，接触面处颗粒的旋转再带动上面几层颗粒的旋转.从图7可以观察到，在一个剪切循环内小颗粒比大颗粒的旋转角度大（在整个土体试样中都有该规律），原因可能是：小颗粒在土骨架中所受约束小，旋转比较自由，而大颗粒受到其他颗粒的挤压，无法自由旋转.
5剪胀体应变的不可逆性体应变
5.1不可逆性体应变的基本规律
在竖向应力较大、颗粒发生破碎时，不可逆性体应变显著.在往返剪切作用下，结构接触面处颗粒发生压密和破碎两种物态演化.颗粒破碎是不可逆性剪胀体应变的主要原因.
5.2颗粒破碎
运用PFC2D黏结模型研究土与结构物在往返剪切作用下的颗粒破碎现象：黏结颗粒（黏结颗粒单元面积等于原来大颗粒的面积）破碎由黏结强度控制，当黏结颗粒受力超过黏结强度时，黏结键断裂，颗粒破碎.图8为考虑颗粒破碎时粗粒土与结构接触面往返剪切试验中体应变随剪切循环次数的变化情况.图8中，体应变总趋势逐渐变小为不可逆性体应变，小波峰为可逆性体应变，可见在考虑颗粒破碎时不可逆性体应变起主导作用.对比图4与8可知，不可逆性体应变大小与颗粒破碎程度密切相关，颗粒破碎程度越大不可逆性体应变越显著.这是因为颗粒破碎是个不可逆的过程，会使颗粒数目、主轴方向、配位数等发生变化，由此产生的宏观试样体应变也是不可逆的.随着剪切循环次数增加，颗粒逐渐破碎，不可逆性体应变增加.通过PFC2D可以得到，体应变总趋势是一直减小的，但体应变变化速率逐渐减小，这是因为连续牢固的土骨架形成后，土颗粒难以进一步被压密及破碎.
6结论
基于PFC2D对粗粒土与结构接触面往返剪切试验的颗粒流数值模拟有以下结论：
（1）接触面体应变可以认为是由一个可逆性体应变分量和一个不可逆性体应变分量构成的.
（2）运用基本圆颗粒的位移场及类长形颗粒的定向试验研究可逆性体应变，发现可逆性体应变是由颗粒平移和自身旋转产生的.位移场试验表明颗粒会围绕一个“旋转中心”位移，“旋转中心”的位置受剪切方向的影响；颗粒定向试验表明剪切作用造成土颗粒转动后的长轴方向偏向于剪切方向一侧.
（3）运用黏结颗粒破碎程序研究颗粒破碎现象，发现随着剪切循环次数的增加，颗粒逐渐破碎，不可逆性体应变增加.通过PFC2D模拟得到，体应变总趋势是一直减小，但剪胀体应变的变化速率逐渐减小，说明不可逆性体应变主要由压密和破碎两种物态演化产生，颗粒破碎起主导作用.
参考文献：
[1]POTYONDY J G. Skin friction between various soils and construction material[J]. Geotechnique， 1961， 11（4）： 339353.
[2]CLOUGH G W， DUNCAN J M. Finite element analysis of retaining wall behavior[J]. J Soil Mech & Foundations Division ASCE， 1971， 97（12）： 16571672.
[3]DESAI C S， RIGBY D B. Cyclic interface and joint shear device including pore pressure effects[J]. J Geotechnical & Geoenvironmental Eng ASCE， 1997， 123（6）： 568579.
[4]池永. 土的工程力学性质的细观研究——应力应变关系剪切带的颗粒[D]. 上海： 同济大学， 2002.
[5]王成华， 占川. 土与结构界面力学特性研究综述[J]. 建筑技术， 2013， 44（6）： 486490.
[6]尚守平， 鲁华伟， 邹新平， 等. 土结构动力相互作用结构自振周期的研究[J]. 地震工程与工程振动， 2013， 33（2）： 117125.
[7]张嘎， 张建明. 粗粒土与结构接触面的可逆性与不可逆性剪胀规律[J]. 岩土力学， 2005， 26（5）： 699704.
[8]周健， 史旦达， 贾敏才， 等. 砂土单调剪切力学性状的颗粒流模拟[J]. 同济大学学报： 自然科学版， 2007， 35（10）： 12991304.
[9]刘文白， 周健. 上拔荷载作用下扩展基础的颗粒流数值模拟[J]. 水利学报， 2004， 35（12）： 110.
[10]杜强， 刘文白. 土与结构物半模直剪试验的颗粒流数值模拟[J]. 水运工程， 2012（8）： 160165.
[11]胡黎明， 马杰， 张丙印. 散粒体间接触面单剪试验及数值模拟[J]. 岩土力学， 2008， 29（9）： 23192322.
[12]蒋明镜， 李秀梅. 双轴压缩试验中砂土剪切带形成的离散元模拟分析[J]. 山东大学学报： 工学版， 2012（2）： 5561.
[13]张翀， 舒赣平. 颗粒形状对颗粒流模拟双轴压缩试验的影响研究[J]. 岩土工程学报， 2009， 31（8）： 12811286.
（编辑贾裙平）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 1:10:55