《基于RBF神经网络的X型四旋翼飞行器优化控制》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于RBF神经网络的X型四旋翼飞行器优化控制

范文

张莹刘子龙

摘要：为使x型四旋翼无人机系统能够在受到扰动时快速调整状态以适应环境变化，对x型四旋翼无人机进行区别于传统的受力分析，建立动力学数学模型，采用RBF神经网络和PID联合控制方法，依靠神经网络自学习和非线性映射特征实现系统控制参数的动态整定。以MATLAB/Simulink为实验平台，对RBF神经网络PID控制系统和单纯PID控制系统分别进行仿真。实验结果表明，RBF神经网络PID控制比传统的PID控制调整时间更短、控制效果更好，增强了系统自适应性。

关键词：x型四旋翼飞行器;神经网络;PID控制;自整定

DOI：10.11907/rjdk.191229

中图分类号：TP301 文献标识码：A 文章编号：1672-7800（2019）012-0051-05

0引言

无人飞行器由空气动力抵消机身重量，飞行控制系统控制其飞行状态或由遥控器控制飞行，从而实现相应空中目标任务，无需人员在机体直接操作。四旋翼无人机（Quadrotor unmanned aerial vehicle，QUAV）是一种通过无线遥控设备控制、机载各种传感器感知无人机姿态实现自主飞行的非载人飞行器，属于典型的非线性欠驱动系统，广泛应用于军事、民用等领域。

目前大多以十字型四旋翼无人机为研究对象，但x型四旋翼无人机姿态变换更加灵活快速，变换过程更加稳定安全，调整更加迅速，并且这种结构不会遮挡前识相机的视线，更加便于加装航拍摄像机等装置，有利于后期开展更加深入的研究工作，所以选择x型四旋翼无人机进行研究。

Altug、Erginer、Bouabdallah、Siegwart等以滑模控制方法为基础设计了无人机滑膜控制器，但该控制器在控制无人机姿态时会不断切换，产生抖动，影响控制效果。GonzOlez lvhn & Tan等利用反步法设计了无人机控制器，但是反步法要求被控对象模型必须精确，所以实际效果往往不理想。文献[10]以Mamdani模型设计了模糊神经网络，但是5层网络结构使网络复杂度增大，训练时间较长。传统PID控制技术具有原理简单、易于实现、控制方便等优点，但是其3个控制参数均为固定值，整定好后无法改变，在非线性系统中想得到良好的控制效果较难。近年来发展的神经网络具有很强的自学习、自适应能力，并且对非线性函数无限逼近，事实上大多数工业工程控制系統均含有某些未知的非线性情况，因此本文将传统PID控制的优势和神经网络的特点相结合，利用RBF神经网络对PID参数进行自整定，使复杂的x型四旋翼无人机非线性系统参数能适应外部环境变化，达到良好的控制效果。

1控制系统数学模型

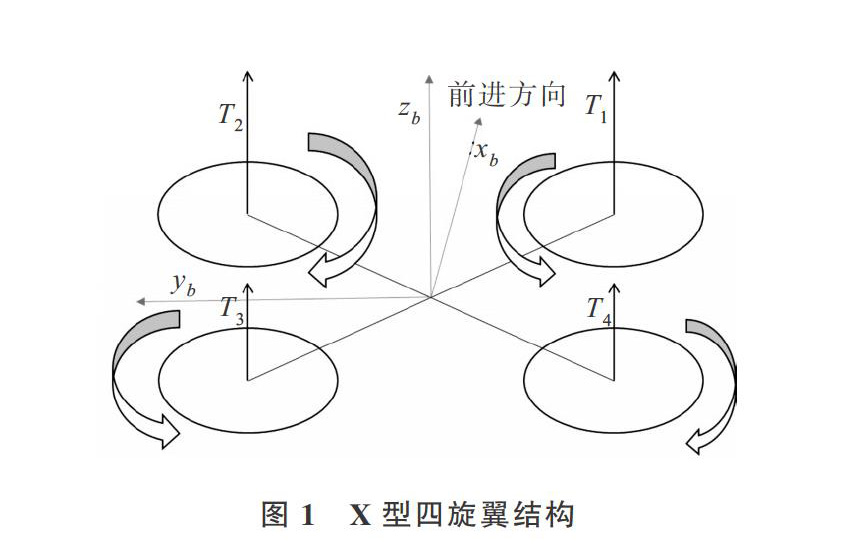
x型四旋翼处于同一对角线上的旋翼为一组，旋转方向一致且区分正反浆，顺时针旋转为正浆，反之为反浆。如图1所示，1、3上的旋翼逆时针旋转，为反桨;2、4上的旋翼顺时针旋转，为正桨。

四旋翼飞行器为了改变飞行器姿态，产生相应的飞行位移运动，通常使用调节多个旋翼之间的转速差方法，使各个旋翼产生相对于质心的力矩。运动分析如下：

垂直升降：同时增加（减小）4个旋翼转速;

俯仰运动：增加（减小）1、2转速，减小（增加）3、4转速;

滚转运动：增加（减小）2、3转速，减小（增加）l、4转速;

偏航运动：增加（减小）1、3转速，减小（增加）2、4转速1。

实际四旋翼飞行情况十分复杂，为对其动力学建模作如下假设：①飞行器为刚体;②质量和转动惯量不变;③飞行器只受重力和螺旋桨升力影响，螺旋桨升力沿Zb向下，重力沿Ze方向;④飞行器重心与中心一致;⑤1、3螺旋桨逆时针转动，2、4螺旋桨顺时针转动。

2RBF神经网络

RBF神经网络属于前向神经网络类型，网络结构为三层的前向网络。第一层为输入层，由输入信号源节点组成;第二层为隐藏层，隐藏层节点数根据具体问题需要而定，径向基函数是对中心点径向对称且衰减的非负非线性函数，是局部响应函数;第三层为输出层，对输人模式作出响应。RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐藏层空间，隐含层对输入矢量进行变换，将低维模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。

四旋翼飞行控制系统是一个典型的多变量、高非线性、强耦合、干扰敏感、欠驱动系统。四旋翼控制系统各通道之间的耦合性、自身不确定性是目前控制系统设计理论中的难点和热点。

虽然传统的PID控制能够在一定条件下整定出最优系统的PID参数，但是现实系统并不是一成不变的，在某种情况下整定好的PID参数到另一种情况或者系统受到干扰时，先前整定的参数便不再适合新的系统，所以参数应跟随系统的变化而变化。RBF神经网络具有非线性映射能力强、收敛速度快等突出特点，由RBF神经网络与经典PID控制器相结合而形成的RBF神经网络PID控制，已应用于PID自整定控制，所以系统选择用RBF神经网络整定PID参数的方法来适应系统状态的改变。因为雅可比矩阵的值直接影响到PID控制器参数的改变，所以RBF实际是通过辨识雅可比矩阵进而改变Kp、Ki和Kd的值，以此调整PID控制器参数进而调整整个系统状态的。如图2所示，RBF神经网络由输入层、隐藏层和输出层三层网络构成，输入层和隐藏层为非线性关系，隐藏层和输出层为线性关系，隐藏层的径向基函数选择为高斯基函数。输入层神经元数为n，隐藏层神经元数为m。

所以优化过程为最小化该代价函数。

（2）误差反向传播。由梯度下降法优化代价函数，J（k）表示误差能量瞬时值，这种对神经元突触权值步步紧逼的调节过程将持续下去，一直到系统达到稳定状态为止，此时学习过程停止。

由式（17）和式（18）得：

在MATLAB环境下对四旋翼的俯仰通道进行仿真实验，给定输入信号为yd（k）=0.50*sin（2*pi*k*ts），用来检测RBF神经网络的辨识能力，结果如图5-图7所示。可以看出，RBF神经网络能够很好地逼近被控对象的实际输出。由于辨识网络开始处于不断寻优过程，所以误差较大。但是RBF神经网络的输出曲线和理想输出曲线大致吻合，证明RBF神经网络对非线性对象具有良好的辨识能力。

RBF神经网络选用3-6-1结构，学习速率为0.1，动量因子系数为0.05，PID参数初始值为Kp=0.03，Ki=0.28，Kd=0.03，PID的学习速率为0.20。当给定输入信号为r（t）=1.0*sign（sin（2*pi*t*ts））时，如图8一图10所示。

系统在0时刻和每次输入变化附近，辨识结果出现较大波动，此阶段为系统自学习寻找PID参数值的过程。将RBF&PID控制器和PID控制器对比，可以看出RBF&PID控制器在姿态控制时其跟踪误差比PID控制器更小、调节时间更短，能更加快速地恢复目标状态。在系统输入发生改变时，神经网络PID控制可以自学习寻找合适的PID参数，在四旋翼飞行过程中遇到扰动之后快速恢复到指定轨迹要求。

5结语

本文以x型四旋翼无人机飞行器姿态控制系统为对象，采用RBF神经网络与传统PID控制相结合的控制方法对系统进行动态控制，有效提升了快速性和鲁棒性，获得良好的控制效果。但本文还停留在仿真阶段，运用于x型四旋翼无人机实际飞行控制还需进一步研究。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。