网站首页  词典首页

请输入您要查询的论文：

　

标题 抵达，而后远航
范文 周卫东 言克琴


[摘 要]“分数的意义”这一课的教学难点是理解单位“1”的含义。通过顺学而导、比较探究、拓展延伸、回顾反思等教学环节，把学生的思维不断引向深处，学生在激烈的思维燃烧、智慧碰撞中，拓展对于分数内涵的深刻理解，体会分数的应用价值。
[关键词]分数的意义；引入；探究；拓展；反思
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）14-0019-03
“分数的意义”是人教版教材五年级下册的内容，教学的重点是让学生明确分数的意义。为了使学生能够初步理解单位“1”的含义，教师要让学生经历分数意义的抽象过程，在建构分数意义的过程中，培养学生分析、综合、抽象、概括的能力，让学生学会用数学思维思考问题。
一、顺学而导，引入新知
师：这节课我们研究什么内容？
生1：分数的意义。
师：三年级时，我们两次学习分数，下面来检验大家学得怎么样。
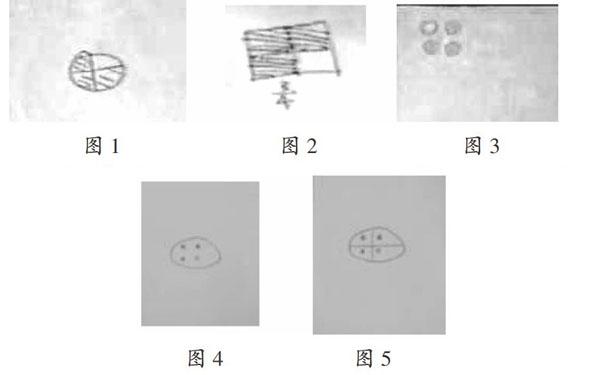
师（板书：）：认识它吗？它表示什么含义呢？换种方式，不用语言表达，在纸片上画一张图来表示的含义。（学生动手操作；教师巡视，并选择有代表性的学生作品进行展示）
师（指图3）：对于这幅作品，大家有什么比较好的建议？
生2：这里的4个圆应该加上一个圈，这样更容易看出“1”在哪里。
师：你的想法与这位同学一样（出示图4），他的作品就有一个圈。还有别的建议吗？
生3：我认为，分数首先要“分”。图4虽然看到了一个整体，但看不出“分”的痕迹。
师（指图4）：我非常同意生3的观点。分数首先要“分”，这张图“分”了吗？哪位同学来把它分一下。
（学生修改图4，得图5）
师：说说你是怎么分的。
生4：我把这4个圆平均分成4份。
师：在研究分数的过程中，有一个特别重要的前提是什么？
生5：前提是要平均分。
师（强调）：这是研究分数的前提，没有平均分就没有分数。
二、比较探究，逐步抽象
1.第一次概括：抽象出单位“1”
师（出示图6）：老师也带来了一幅图，这幅图可以表示嗎？
生（齐）：可以！
师：在刚才的作品中选择两幅，再加上老师的这一幅，编上号①②③（如图7、8、9）。三幅作品的画法不一样，为什么都能表示？它们有什么相同的地方？
生1：都是把一个整体平均分成4份，取其中3份。
师：善于比较、求同存异是学习数学的一项重要的基本功。大家再比较①②③号图形有什么不同的地方。
生2： ③号图是线段图，①号和②号都不是线段图。
生3：它们的形状不同。
生4：①号图分的是一个物体。
师（板书：一个物体）：既然①号图分的是一个物体，那②号图呢？
生5：②号图分的是4个物体。
师：分的物体只能是4个吗？画8个行不行？画10个呢？
生6：可以。
师：那②号图可以怎么概括？
生7：把多个物体平均分成4份。
师：对，这是三年级下册所学习的知识，你们的领悟能力特别强！那③号图中的这条线段代表什么呢？
生8：质量单位。
师：如果把这里的1吨换成1米、1小时、1平方米，行不行？
生（齐）：可以！
师：谁能说说③号图中的这条线段实际上代表什么？
生9：一个计量单位！
师：其实一个物体、一个计量单位和多个物体组成的一个整体，它们都有一个共同的名称，就是单位“1”。
师：回过头看一看，单位“1”有哪几种类型呢？
生10：单位“1”有一个物体、一个计量单位、多个物体组成的一个整体共三种类型。
师：还能再举一些单位“1”的例子吗？
……
2.第二次概括：抽象出的意义
师：理解了单位“1”，谁来说说的含义？
（教师把的意义补充完整并板书，让学生完整地说出 的意义）
3.第三次概括：抽象出分数的意义
师出示：
师：每个句子里的单位“1”分别是什么？分数表示什么含义？
生11：第（1）句是把全班学生人数看作单位“1”， 把单位“1”平均分成9份，表示这样的5份，就是。
生12：第（2）句把地球表面积看作单位“1”，平均分成100份，海洋面积是其中的71份。
师：这句话里面还隐含了另外一个分数，你能找到吗？
生13：地球表面有的面积被陆地覆盖。
师：真棒！能看到表面的数学，还能找出隐藏在文字里面的数学，这是比较高级的学习方式。
生14：第（3）句是把1小时看作单位“1”，平均分成3份，小明做家庭作业用了这样的1份。
师：我们研究了这么多的分数，如果继续研究下去，能研究得完吗？
生（齐）：研究不完。
师：那能不能概括出什么是分数呢？
生15：把单位“1”平均分成x份，表示其中的x份。
师：你有很强的符号意识。如果用文字来表示呢？
生15：若干份。
师：表示这样的……用什么词好呢？
生16：1份或几份。因为把单位“1”平均分成若干份，表示的可以是1份，也可以是几份。
师：现在让我们自豪地把分数的意义完整地读一遍。要提醒大家的是，读的时候把你认为重要的词加重语气。现在回顾一下，我们是怎么概括出分数的意义的？（生答略）
师：说得太好了！是的，我们以“变”与“不变”为线索，研究出了分数的意义。其实，分数的知识中还有许多的“变”与“不变”，让我们来一起学习吧。
三、拓展延伸，意义建构
1.分一分
师出示：
师：这里的单位“1”有12个圆片，其中有一部分涂了颜色，请你先分一分，再用表示出来。

生1：把单位“1”平均分成3份，涂色部分表示其中1份，就是（如图10）。
生2：把单位“1”平均分成6份，表示其中的2份，用表示（如图11）。
生3：把单位“1”平均分成12份，表示这样的4份，就是
（如图12）。
师：比较图10、11、12，什么变了，什么没变？
生4：图10是把单位“1”平均分成3份，阴影部分表示这样的1份；图11是把单位“1”平均分成6份，阴影部分表示这样的2份；图12是把单位“1”平均分成12份，阴影部分表示这样的4份。
生5：单位“1”没变，阴影部分的数量也没变。
师：同样的单位“1”，不同的分法就能得到不同的分数。还有没有其他发现？
生6：分的份数越多，每一份代表的数就越小。
生7：这三种分法中，阴影部分没变，三个分数的大小应该是相等的。
师：真了不起！这是我们将要学习的内容，你现在已经有所感觉了！
2.游戏
师：分圆片中有“变”与“不变”，游戏中也有“变”与“不变”呢！
（1）游戏一：按要求取物
师（拿出A、B两个袋子，袋子中装有一些圆片，分别发给两位学生，让他们数一数一共多少个）：请拿A袋的同学和拿B袋的同学各取出袋中圆片的摆到黑板上。（拿A袋的学生贴出5个，拿B袋的学生贴出3个）
师：同样是，为什么A袋取了5个，而B袋只取3个？
生8：两个袋子的单位“1”不一样。
师：大家算一算，A袋的单位“1”是多少？B袋的单位“1”又是多少？
生9：A袋10个，B袋6个。
师：请两位同学把袋子里的圆片都摆上黑板，公布答案。
师：请拿A袋的同學取出，拿B袋的同学取出。（两个学生都摆出2个圆片）
师：对于他们取的结果，如果你是数学老师，你可能会问一个什么数学问题？
生10：为什么分数不一样，拿出的个数却是一样的呢？
师：你真有做小老师的天分，跟我要问的问题是一样的。谁能回答这个问题？
生11：因为它们的单位“1”不一样。
师（小结）：不一样的单位“1”，不一样的分数，但是它们取出的个数可能是一样的。
（2）游戏二：挑战未知
师出示：
师：把刚才A、B两个袋子里的16个圆片都摆在一起，组成一个大的单位“1”。
师：如果要你取圆片，你打算取几个？方框里填几？（生答略）
师：谁能看出这两则游戏里的“变”与“不变”呢？
……
四、回顾反思，全课总结
师：通过这节课的学习你有哪些收获呢？
……
【赏析】
细细品味周老师的这节课，深深地感到：如果把每一节课看作是一段难忘的旅程的话，那么周老师的这节数学课所实现的不仅仅是知识的抵达，更是儿童思维发展和生命成长的远航。
1.启锚：知识的生长点与学情基点
奥苏伯尔曾说：“如果让我不得不把所有教与学的原理还原成一句话的话，那就是要知道学生已经知道了什么，然后在已有知识的基础上进行教学。”要让学生的学习真正发生，最关键之处就是要摸准他们学习的真实起点，找准他们“现在在哪里”。本节课是在学生初步认识分数的基础上教学分数的，需要学生能够完整地概括、抽象出分数的意义，这正是学生学习分数的一个难点。周老师打破常规思路，创造性地从切入，引导学生根据已有的知识积累，从平均分一个物体，自然生长到平均分由多个物体所组成的整体，不断逼近“单位1” 这一核心概念。然而，对于的表述，班上没有一个学生能给出完美答案，周老师不急不忙，顺学而教，引导学生将多幅接近分数意义的图形进行比较、修正，使学生最终领悟“整体”的概念，为理解分数的意义做好准备。
2.抵达：知识的核心处
维果茨基的“最近发展区”理论认为：支架式学习是指围绕事先确定的学习主题，建立一个概念框架，把学生的学习从一个水平引向另一个水平的学习方式。根据以往的教学经验，要让学生深刻地理解并准确地表达出分数的意义十分困难，对此，教师要善于帮助学生积累根的知识储备，激活学生相关的活动经验，让分数的意义在丰富的土壤中自然地生长出来。周老师巧妙地引导学生分三次来概括分数的意义：先围绕单位“1”的三个层次的内涵（一个物体、一个计量单位、多个物体组成的一个整体）抽象出“单位1”；再在单位“1”概念的基础上概括出的意义；最后，概括出“若干份”“一份或几份”和分数的意义。这样的教学，源于教材，基于学情，细致严谨、环环相扣，一步一步地逼近和抵达分数的核心知识，学生自然理解到位。
3.远航：驶向思维的纵深处
周卫东老师一直倡导一个观念：教学，不能囿于抵达，更要能远航！是的，教学追求被吸引，美丽的风景在远方。本节课的教学，在概括了分数的意义之后，学生思维的脚步并没有停下，而是在多层问题情境的作用下不断发酵、孕育与生长。“分12个圆片”的设计，能引导学生在“变”与“不变”的辩证思维中感悟“在总数不变的情况下，分的份数与每份数的大小变化、分子分母的变化与分数值大小关系”，为后续分数基本性质的学习做了很好的铺垫。而“游戏”环节的设计，把学生的思维不断引向深处。这两个教学环节不但隐含了众多的思维发散点，更是指向分数问题的解决。学生在激烈的思维燃烧、智慧碰撞中，深刻理解了分数的内涵，逐步完善了对分数知识的建构。
（责编 金 铃）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 4:28:27