网站首页  词典首页

请输入您要查询的论文：

　

标题 一种改进的C4.5决策树算法
范文 胡美春　田大钢



摘 要：为了提高C4.5决策树算法的有效性，提出一种改进的C4.5决策树算法。结合粗糙集理论的属性约简算法和Fayyad边界点判定定理，对C4.5算法进行了改进，利用UCI数据集进行了实验。结果表明，改进的C4.5算法不仅提高了准确率，而且缩小了决策树规模，减少了分类时间。
关键词：C4.5决策树算法；粗糙集；属性约简；连续属性；分割阈值
DOIDOI：10.11907/rjdk.151479
中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2015）007-0054-03
0 引言
决策树方法在分类、预测、规则提取等领域应用广泛。构造决策树的算法有很多种，其中最具影响力的决策树算法是ID3算法[1]和C4.5算法[2]。ID3算法是由Quinlan于1979年提出来的，C4.5算法是由Quinlan于1993年在ID3算法的基础上提出来的，保留了原有算法的优点并改进了原算法的缺点。但是，C4.5算法仍然存在一些不足，比如在处理现实数据时，数据集中存在很多与决策属性关联性很小甚至毫无关联的冗余属性；连续属性值处理过程中最优分割阈值选择比较耗时等等。因此，本文提出一种改进的C4.5算法，通过实验将它与传统的C4.5算法进行比较与分析，以此来说明改进算法的优越性。
1 C4.5算法原理
C4.5决策树算法主要利用信息熵原理，选择信息增益率最大的属性作为分类属性，递归地构造决策树的分支，完成决策树的构造[3]。它是在ID3算法的基础上提出来的。
ID3算法的基本原理[4]如下：设E=F1×F2×F…×Fn是n维有穷向量空间，其中Fi 是有穷离散符号集。E中的元素e={V1，V2，…Vn}称为样本空间的例子，其中Vj∈Fi，（j=1，2，…n），为简单起见，假定样本例子在真实世界中仅有两个类别，在这两个类别的归纳任务中，PE和NE是实体分配，称为概念的正例和反例。一样本集被一棵决策树作出正确分类所需要的信息量为：
I（P，N）=-PP+NlogPP+N-NP+NlogNP+N（1）
如果选择属性A作为决策树的根，A取V个不同的值{A1，…，An}，利用属性A可以将E划分为V个子集{E1，…Ev}，其中Ei（1≤i≤V）包含了E中的属性A取Ai值的样本数据，假设Ei中含有pi个正例和n个反例，那么子集Ei所需要的期望信息是I（pi，ni），以属性A为根，所需要的期望熵为：
E（A）=∑Vi=1pi+niP+NI（pi，ni）（2）
其中，
I（pi，ni）=-pipi+nilogpipi+ni-nipi+nilognipi+ni（3）
以属性A为根的信息增益为：
Gain（A）=I（P，N）-E（A）（4）
对样本集T，假设A有s个不同取值的离散属性，划分为s1，s2，···，sn共n个子集，用A分割样本集所得的信息增益算法与ID3一样，分割信息量为：
S（s，A）=-∑ni=1sislog2（sis）（5）
信息增益率为：
GainRatio（s，A）=Gain（s，A）S（s，A）（6）
C4.5算法的基本原理与以上ID3算法的基本原理类似，唯一不同的是ID3算法是选择信息增益最大的属性作为测试属性，而C4.5算法是按公式（6）计算信息增益率。选择具有最高信息增益率的属性作为测试属性，较好地解决了ID3算法的多值属性偏向问题。
2 基于粗糙集理论的属性约简
1982年波兰数学家Z.Pawlak提出了一种新的数学工具，主要用来处理不确定性和模糊性问题，它就是粗糙集（Rough Set）理论。和处理不确定性问题的数学工具相比，粗糙集理论具有一定的优越性。比如，它在处理数据时，并不需要关于数据的任何已知的或额外的信息；另一个特点则是它能表达和处理不完备信息，能够通过属性约简推导出知识的最小表达。
2.1 粗糙集概念
定义1：一个四元组S=（U，A，V，f）可以用来表示一个信息系统，对象的非空有限集合为U，即论域U = {x1， x2， …， xn}；A为属性的非空有限集合；通常将属性集分为两类，A=C∪D，C∪D=Φ，C称为条件属性集合，D称为决策属性集。 V=∪a∈AVa，Va是属性的值域；f：U×A→V是一个信息函数，即a∈A，x∈U，f（x，a）∈Va。一个关系数据表格可以用来表示一个信息系统，表格的行代表论域中的对象，列代表对象的属性。表中一行属性的值反映一个对象的全部信息。
定义2：在一个已知的信息系统中，对于属性集RA且R≠Φ的不可区分关系IND（R）定义为：IND（R）={（x，y）|（x，y）∈U×U且a∈R，有f（x，a）=f（y，a）}，若（x，y）∈IND（R）， 则称x和y是R不可分辨的。显然IND（R）是一个等价关系，记作U/IND（R）={[x]p：x∈U}，简记为U/R，其中：[x]p={y∈U|（x，y）∈IND（R）}。
定义3：对于一个给定的知识表达系统S=（U，A，V，f），每个XU和一个不可区分关系RA，X的上近似和下近似分别定义为：，apr（X）=∪[x]R∩X≠Φ[x]R={x：[x]R∩X≠Φ}，apr（X）=∪[x]RX[x]R={x：[x]RX}，X的正域定义为：POS（X）=apr（X）。
2.2 粗糙集的属性约简
定义4：一个属性a的重要性（P对U有一个分类，R对U也有一个分类，如果分类完全相同，则P，R对于分类来说是一样的）可以利用两个属性集合P，R之间的相互依赖程度来确定。属性集P对R的依赖程度用γR（P）表示，定义如下：
γR（P）=card（POSR（P））card（U），POSR（P）=∪X∈U/IND（P）aprR（X）
其中card（.）表示集合的基数，POSR（P）是属性集R在U/IND（P）中的正区域。
定义5：属性a加入R，对于分类U/IND（P）的重要性程度为：SGF（a，R，P）=γR（P）-γR-{a}（P）。
定义6：在信息系统S=（U，A，V，f）中，PA，且P是独立的，满足IND（P）=IND（A），则称P是A的一个约简，用RED（A）表示P的所有约简集合；如果P中的所有元素在A中不可省略，则称P是A的核，记为Core（A），显然Core（A）=∩RED（A）。
3 C4.5决策树算法改进
3.1 算法改进思想
3.1.1 属性约简基本思想
粗糙集理论中进行属性约简的方法有很多种，本文采用的是基于属性重要性的属性约简方法，基本思想为：
依据定义4计算决策表中决策属性对条件属性C的依赖程度γc（D），如果POSc（D）≠POSC-{c}（D），表示该属性为核属性，将此属性加入核属性集Core（D）；依据定义5分别计算每个属性相对于核属性集的重要性程度，选择重要性程度最高的属性与属性核集进行合并，作为当前约简结果集，直到约简集能够保持相对约简为止，输出约简结果；否则继续计算，相对约简的标准为IND（RED）=IND（D）。
3.1.2 连续数据离散化过程改进基本思想
C4.5算法在连续属性离散化过程中，需要对属性的所有划分进行预测，这一计算量很大，将占有很多时间，如何快速定位连续属性的最佳分割点已成为亟待解决的问题。根据Fayyad[5]边界点判定定理，无论数据集有多少种分类，无论数据分类怎样分布，连续属性的最佳划分点总是出现于连续序列中两个相邻异类实例的边界点上[6]。所以，在对连续属性进行离散化过程中，不需要对每个阈值点比较，只要比较相邻不同类别的边界点即可。例如，当排序后的实例属性值为{v1，v2，···，v10}，其中前3个属性类别C1，后3个属于类别C2，最后3个属于类别C3，只需要检查两个边界点v3和v7，无需检查其余7个阈值点，然后选择v3和v7中使得平均类熵最小的那个作为最优阈值[7]。
3.2 改进算法描述
输入：决策系统S=（U，V，F，C∪D）
输出：决策树
（1）对决策树系统进行规范，依次对每个属性从1开始逐个编号，每个属性的取值范围也从0开始逐个编号。
（2）根据定义2计算不可分辨关系U/IND（R），就是将相同条件属性值的实例分在同一个组，形成若干个这样的组，从而构成U上的一个划分，用二维数组IND的每一行存放每一组实例。
（3）根据定义3计算条件属性C的正域POSC（D）。扫描IND数组的每一行，如果存在决策树属性值不一样的实例，就将这一行删除，POSC（D）就为剩下的实例集合。
（4）根据定义4计算决策表中决策属性对条件属性C的依赖程度γc（D）。
（5）令核属性集Core（D）=φ。
（6）对每个条件属性c计算POSC-{c}（D），如果POSc（D）≠POSC-{c}（D），则Core（D）=Core（D）+{c}。
（7）令约简集RED=Core（C）。
（8）如果IND（RED）=IND（D），则输出最小约简集RED，否则对每个C-RED的属性p，计算属性重要性SGF，选择属性重要性程度最大的加入到RED中，如果同时存在多个属性达到最大值，则从中选择一个属性值组合数最少的属性加入到RED中，重复第（8）步直至输出最终约简集RED。
（9）利用以上得到的最小约简属性，得到新的数据样本集合，作为算法的数据输入。
（10）利用传统算法中的方法创建节点，如果样本集中存在连续型属性时，则使用改进的离散化方法进行处理。
（11）对样本集重复进行步骤（10）操作，直至分支样本集中全为同一类别或者样本集为空。
3.3 实验结果分析
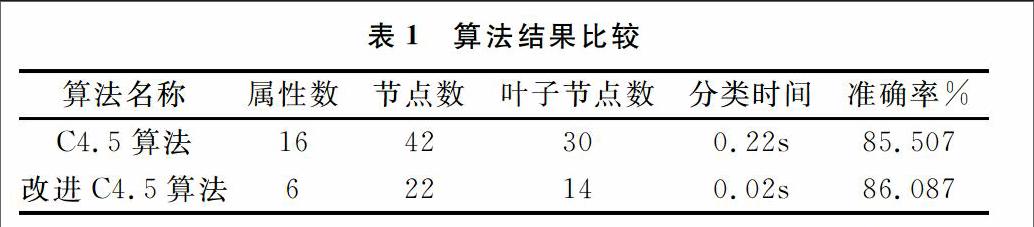
为了验证改进算法的优越性， 在Win7系统和WEKA 3.6.9平台下，利用UCI数据集中的Credit-a数据集进行具体分析和验证。Credit-a数据集包括690个样本，共16个属性（包含了决策属性），其中有6个连续型属性，有2类。首先，分别对每个属性和属性的取值范围逐个编号，利用上述的粗糙集属性约简算法对该数据集进行属性约简，约简后决策表中仅剩6个条件属性：A2、A6、A7、A9、A14和1个决策属性class，然后采用改进的C4.5算法对约简后的数据集进行分类（其中70%作为训练样本，30%作为测试样本），分别利用传统的C4.5算法和改进的C4.5算法进行分类，对比分析与比较两种算法的结果，如表1所示。
结果显示，改进的C4.5算法得到的决策树比传统的C4.5算法小，属性个数从16降到了6，减少了数据冗余，节点数从42减到了22，叶子节点数也从30减到了14，决策树的规模得到了优化；分类时间从0.22减少到0.02，提高了分类效率；分类准确率则从85.507%提高到86.087%。因此，可以看出改进的C4.5算法不仅缩小了树的规模，提高了分类效率，而且提高了分类准确率。
4 结语
本文提出一种改进的C4.5决策树算法，不仅利用粗糙集理论中的属性约简方法对决策表中的条件属性进行了过滤，去掉大量冗余属性，减少噪声，而且对连续属性离散化过程进行了改进，将约简后的数据作为输入，得到最终分类结果。实验数据表明，改进的C4.5决策树算法不仅缩小了决策树规模，而且提高了分类准确率和决策树构造效率。该改进算法对今后决策树算法的研究与应用具有一定的指导意义。
参考文献：
[1] QUINLAN J R. Induction of decision tree[J].Machine Learning.1986，1（1）：81-106.
[2] QUINLAN J R. C4.5：Programs for machine learning[J].San Mateo：Morgan Kaufman Publishers Inc，1993：27-48.
[3] 李强.创建决策树算法的比较研究——ID3，C4.5，C5.0算法的比较[J].甘肃科学学报，2006 （12）：84-87.
[4] 蔡丽艳.数据挖掘算法及其应用研究[M].成都：电子科技大学出版社，2013：20-26.
[5] FAYYAD U M，IRANI K B.On the handling of continuous-valued attributes in decision tree generation[J].Machine Learning，1992，8（1）：87-102.
[6] 姚亚夫，邢留涛.决策树C4.5连续属性分割阈值算法改进及其应用[J].中南大学学报：自然科学版，2011，42（12）：3772-3776.
[7] 乔增伟，孙卫祥.C4.5算法的两点改进[J].江苏工业学院学报，2008，20（4）：56-59.
[8] 黄爱辉.决策树C4.5算法的改进及应用[J].科学技术与工程，2009，9（1）：34-36，42.
[9] 李孝伟，陈福才，李邵梅.基于分类规则的C4.5决策树改进算法[J].计算机工程与设计，2013，34（12）：4321-4325，4330.
[10] 赵卫东，李旗号.粗糙集在决策树优化中的应用[J] .系统工程学报， 2001， 16（4） ：289-295.
[11] 向卓元，张蕾.粗糙集理论对C4.5算法的优化研究[J].电脑知识与技术，2012，8（16）：3782-3785.
[12] 刘鹏.一种健壮有效的决策树改进模型[J].计算机工程与应用，2005（33）：172-175.
[13] QINGYUN C. Research on incremental decison tree algorithm[C].2011 International Conference on Electronic & Mechanical Engineering and Information Technology，2011.
[14] 屈志毅，周海波.决策树算法的一种改进算法[J].计算机应用，2008，28（S1）：141-143.
[15] 周剑锋，阳爱民，刘吉财.基于改进的C4.5算法的网络流量分类算法[J].计算机工程与应用，2012，48（5）：71-74.
[16] 刘晓宇.C4.5算法的一种改进及其应用[D].青岛：中国海洋大学，2013.
（责任编辑：杜能钢）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/6 3:04:48