《面向业务需求的航空白组网连通性研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

面向业务需求的航空白组网连通性研究

范文

刘岩松郑欣王金涛龙岩

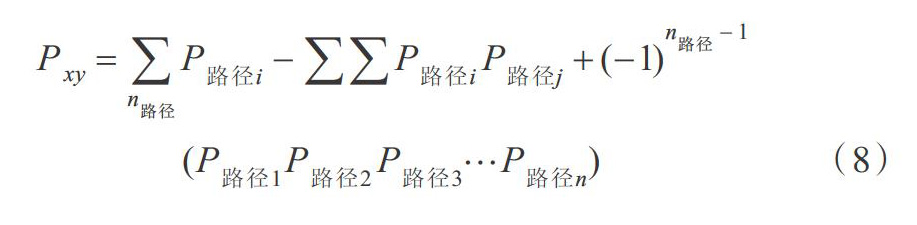
摘要：为满足不同业务需求，保障业务实时性与稳定性，针对多种业务不同的链路连通性，提出适合不同业务的链路选择方法。基于航空自组网近似模型，首先提出一种节点到基站的连通概率算法，其次根据飞机非匀速运动特点，运用Gauss-Markov移动模型，求出航空自组网连通时间，同时建立相应场景并进行仿真。结果表明，不同业务可根据程序计算结果选择所需链路。

关键词：链路;航空自组网;连通概率;连通时间

DOI：10.11907/rjdk.192222 开放科学（资源服务）标识码（OSID）：

中图分类号：TP393文献标识码：A 文章编号：1672-7800（2020）006-0240-04

0 引言

航空自组网（AeronauticalAd Hoc Networks，AANET）的出現推进了民航通信系统发展，它既可提供空中紧急救援、航行管理，还可提供机上娱乐、语音通信、因特网接人等服务。航空紧急救援是目前最有效的应急救援。德国空中救援组织要求空中紧急救援响应时间在8min之内，在过去的30年里，该组织已完成十万多次空中急救任务，有近90万人获得急救，其中10多万人因得到空中快速抢救得以生还，不过仍有近万人因空中救援响应不及时而丧生。选择较高连通概率链路可缩小救援响应时间，从而提高飞行活动安全性和可靠性。除了航空紧急救援，机舱内娱乐业务和语音通信等服务也依赖于飞机链路稳定性，自2013年来，中国国际航空实现运行第二代机上无线网络系统，该系统拥有5个高性能处理器，存储容量达到1T，每个AP可为50-70位旅客提供更丰富的娱乐内容。但机上娱乐等高带宽业务需消耗少则几十兆多则上千兆流量，航空白组网连通时间较长。所以不同业务选择合适的链路尤为重要。

许多学者围绕航空自组网连通性进行了研究。文献[5]提出一种甚高频航空自组网的解决方案，解决了飞行器之间不能直接通信、难以接人Internet等问题;文献[6]提出一维航线连通概率公式以解决固定航线航空自组网连通性问题;文献[7]提出交叉航线连通问题解决方法。但现有研究均存在理论与实际结合不紧密、研究场景只针对一维航线场景、节点没有固定的运动轨迹等问题。

针对以上问题，本文首先建立航空自组网空中航线模型与空地航线模型，提出节点到基站连通概率计算方法;然后结合飞机非匀速运动的特点，基于Gauss-Markov移动模型，求出航空自组网连通时间，结合不同业务需求，建立相应场景进行仿真实验。结果表明，不同业务可选择合适的链路，保证相关业务稳定地完成。

1 模型建立

假设两架飞机之间通讯半径为R，即飞机节点之间必须小于或等于R才可连通，飞机数量服从泊松分布。

（1）模型1（空中航线模型）。空中航线模型大多采用双向航线模型，如图1所示。航线高度根据飞机飞行方向分成奇偶高度层，相邻两层的飞机飞行方向相反，且飞机之间相互独立。

（2）模型2（空地航线模型）。空地航线模型表示为飞机与地面基站的通信模型，如图2所示。图中场景共有3条航线分别为A、B和C。地面有4个通讯基站，分别为a、b、c、d。飞机经过多跳直接或间接接人地基站，例如航线A上的飞机通过节点1跳到航线C，再通过节点1通信范围内航线上的节点，最终接人地面基站d。

2 连通概率计算

基于航空自组网模型，计算节点到地面基站的连通概率，具体计算流程如图3所示。本部分以图2为例，详细说明连通概率具体算法。

2.1 初始概率

航线A上的飞机节点跳到其通信范围内的航段H1n上等同于其通讯范围内至少有一架飞机的概率，而任意一条航线飞机数量服从泊松分布，以坐标为（x，Y）的飞机节点为开始节点，计算其跳到通信范围内航段H1n的概率，记为P初始，如式（1）所示。

其中，λb是航线B上的飞机密度，n是飞机总数。

2.2最后一跳概率

2.3 跳跃概率

如果航段h1n.最后在地基站的通信范围内，则可直接计算最后一条概率;否则，分别计算航段h1n。上n个点的坐标概率，记为跳跃概率P跳跃，如公式（3）-（5）所示。

2.4 任意两个节点连通概率

通过上述步骤得到节点（x，y）到地基站的所有路径概率，如公式（7）所示。

记路径i=（1，2…n），存在事件i，事件i发生的概率为P路径。至少有一个事件发生的概率即为节点到地面基站的连通概率，使用概率论加法公式，如式（8）所示。

3 连通时间计算

3.1 链路连通时间

在航空自组网中，群组移动是随机的，且会影响前后节点速度。Gauss-Markov模型相比于其它群组，移动模型具有前后运动相关性，每隔一段时间即根据当前速度改变一次，第n次运动由第n-1次运动速度值和一个随机变量决定，如式（9）所示。

其中，vn表示节点在第n个步骤的速度值，a表示趋近于无穷大时的平均值vn-1，其符合高斯分布随机变量∝ ∈[0，1]，用来调节运动随机性，根据相应的速度公式可以求出连通时间。假设其中一个节点速度为v1，另一个速度值为v2，两个节点距离为D，因为只有当飞机之间的距离小于通信距离才会实现全联通，假设两个飞机之间的通信距离为R，则有限制条件D

当两个飞机位于单条航线上，两个飞机方向相同，距离为：

3.2 信息所需连通时间

信息大小约为C，链路传递速率为s1，根据公式（14）可求得信息所需连通时间。

链路连通时间与信息连通时间不同，通常链路连通时间大于信息所需时间，才可顺利传输信息。

4 仿真环境

以航空白组网的空中航线模型和空地航线模型为背景，结合不同业务需求，在MATLAB平台上构建仿真场景。仿真包括两组实验：场景l以空地航线模型为背景，模拟飞机出现故障的紧急情况;场景2以空中航线为背景，模拟鄰近飞机信息传递情况。

4.1 仿真场景1

假设一架A320飞机有一名因消化道大出血导致失血性休克的患者，机组人员急需与地面基站取得联系，此时飞行场景大小为1000km x 1000km，航线数目为6，飞机通信半径300km，航线长度800km，飞机间安全距离40km，基站坐标（450kin，250km）。航线参数信息如表1所示。

使用本文提出的多航线航空自组网连通概率计算方法，得出该场景下最大概率链路，如图4所示。

如图4所示，以黑色三角为飞机起始点，根据泊松分布计算第一跳概率，以此为圆心，通信范围为半径，得到与周围航线相交的离散点。分别计算这些离散点转移概率，其中点5连通概率最大，以此作为下一跳，最后直接接人地面基站，该路径为最大概率链路。各链路概率值如表2所示。

根据概率值得出不同链路连通概率与时间的关系，如图5所示。其中横坐标为连通时间，单位为s，纵坐标为连通概率。

由图5可以看出，A320发生紧急情况时，为实现快速与地面取得联系，应在周围5条可连通的链路中，选择最大概率的链路。

4.2 场景2

假设飞机1上乘客A正在通过航空自组网给另一架飞机5上的乘客B传送视频。视频大小约50M，飞行场景大小为600km x 800km，航线数目3，飞机相互之间距离均在通讯半径内。分别根据表3的飞机参数和表4的链路参数，求出链路连通时间和信息连通时间，再进行对比，如表5所示。

通过表5可知，这3个链路中飞机链路1-2-5和飞机链路1-3-5的带宽较大且连通时间大于信息传递时间，可以实现信息传递。其中飞机链路1-2-5本身连通时间较长，稳定性更强，所以选择飞机链路1-2-5。

综合以上分析可得出该场景下飞机最长连通时间路径，如图6所示。

飞机l向飞机5传送视频时，因流量较大，需较长的连通时间链路，在周围3条链路中，应选择链路1-2-5。

5 结语

本文针对不同业务有不同链路连通性的需求，结合航空自组网空地模型和空中航线模型，提出了节点到基站连通概率算法，并应用Gauss-Markov移动模型，求出航空自组网飞机节点间的连通时间。不同业务根据计算结果选择对应链路可保证业务高效稳定地完成。本文对于业务类型涉猎有限，因此下一步将使航空白组网与更多类型业务结合，为航空白组网连通性研究提供重要参考。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。