《基于汉诺塔游戏的递归算法解析》-工学论文，软件工程论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

基于汉诺塔游戏的递归算法解析

范文

朱翠苗++庾佳++周玲余++金静梅

摘要：递归是计算机语言课程中经常遇到且较为重要的一个问题，对此问题的讲解是否清楚、是否真正掌握对日后的程序学习都会产生较大影响，本人将结合教学中讲解递归程序时使用的方法，探讨如何更好地理解递归思想，从而为学好高级程序语言打下坚实的基础。

关键词：递归；嵌套；栈

中图分类号：TP3 11.5

文献标识码：A

DOI： 10.3969/j.issn.1003-6970.2015.11.008

0 引言

汉诺塔（TowerotHanoi）问题起源于这样一段故事：在创世纪时，Benare有一座波罗教塔，由三根钻石柱子支撑，神在第一根柱子上放置了64枚上小下大依次排列的金盘子，令门徒将所有的金盘子从第一根柱子可经第二根移至第三根柱子上.且搬运过程中遵守上小下大的原则，若每天只搬运一枚金盘子，当金盘子全部搬运完毕之时.此塔将会毁灭，就是世界末13来临之时。

递归关系作为数学与计算机科学的一个重要研究对象，特别是在算法分析中有着广泛的应用。Hanoi塔问题直观地演示了递归过程。

1 递归算法简述

在高级程序语言语言中，函数和过程除了可以调用其它子程序外，还可以直接或间接地调用自身，这种情况称为递归调用。递归是一种特殊的函数调用，其特殊性在于自己调用自己，且该种调用深度一般较深，对该问题的理解一直是高级程序语言学习中较为困难的一部分，同时，该问题又是非常重要的，因为学生对该类问题的掌握程度将直接影响到学生今后的学习，以及后续课程教师教学工作的正常进行。因此无论是学生还是教师对该类问题的掌握就显得尤为重要。

2 算法的解析过程

对该问题的理解应抓住以下几个环节：

2.1 函数调用与返回过程

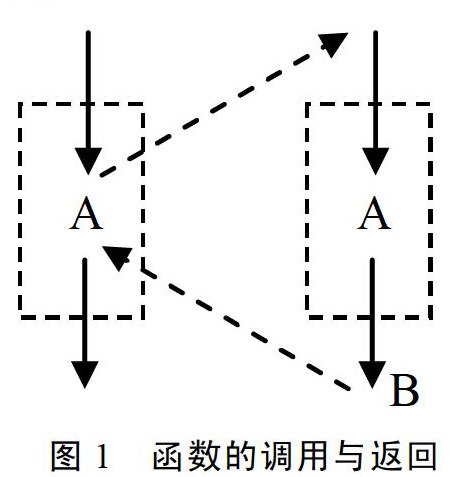
在函数调用与返回问题的讲解中最主要的应讲清断点A、B处（下图所示）所完成的工作。

（1）调用过程

在调用过程转向被调过程的断点A处程序做了以下几件事：

②存信息，一般是指调用过程传递给被调用过程的实参，及由被调过程返回调用过程的返回地址；

③将控制转向被调过程；

（2）返回过程

由被调过程向调用过程返回的断点B处也可理解为程序做了以下几件事：

①保存返回信息，主要是被调过程传递给调用过程的信息，如计算结果等；

②将控制按返回地址返回调用过程处；

2.2 递归过程

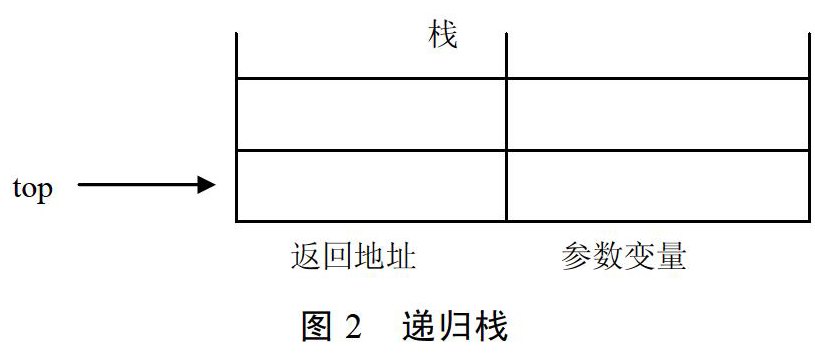
递归即是函数调用的嵌套，对于该问题的讲解，结合具体例题，递归过程中引入“递归栈”的概念。

由“后调用，先返回”的原则很自然地引出“栈”，因前面已讲过在调用过程时要保存返回地址，在上例中共保存了四个地址，那么在返回时具体返回到哪个地址呢？因为递归调用遵循“后调用，先返回”原则，所以应返回到在它之前最后保存的那个地址，即：后保存的先用，这下好符合栈的“先入后出，后入先出”操作原则。同时还应向学生讲清楚“递归栈”不只存放返回地址，它还是实参和临时变量的存储空间。

3 实例讲解

根据以上所述，在讲解具体的递归程序时，关键抓住两点：①用图示的方法画出函数、过程调用的嵌套图；②附设一个“递归栈”，根据题意可看出“栈”中的内容是不断变化的，再结合嵌套调用的示意图，就可轻松地把递归程序向学生讲解清楚。下面我以经典的HANOI塔问题为例。

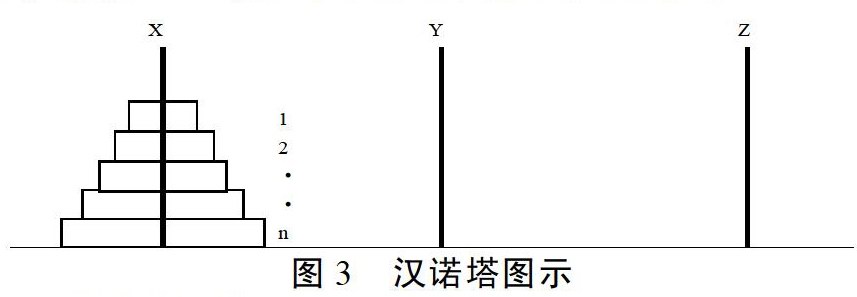
假设有三个命名为X，Y，Z的塔座，在塔座X上插有n个直径大小各不相同依小到大编号为1，2，……，n的圆盘（见图），现要求将X塔座上的n个圆盘移至Z塔座上，并按同样的顺序叠排。

程序代码如下（C语言实现）：

#include

void move（char x，char y）{

printf（“%c一>%c＼n”，x，y）；

}

void hanoi（int n，char one， char two， charthree）{

if（n==1） move（ one，three）；

else{

hanoi（n-1，one，three，two）；

move（one， three）：

hanoi（n-1，two，one，three）；

）

main（）{

int m；

printf（“input the number of disks：”）；

scanf（“%d”，&m）；

printf（"the step to moving %3d diskes：＼n"，m）；

hanoi（m，‘A，‘B，‘C）；

}

现在我详细分析3个圆盘的hanoi塔问题的递归函数是如何来执行的，即上面的程序当total为3时的过程。

（1）首先执行主函数，当运行到hanoi（total，x，y，z），系统产生一个递归栈，调用地址、变量和参数的值被压进栈中。

（2）系统调用函数hanoi（3，x，y，Z），系统开始执行函数体内语句，显然n=1不成立，系统执行else后的语句，hanoi（2，x，z，y），此时我们不妨假设看成函数的嵌套调用，又调用了一个函数hanoi（2，x，z，y），系统再把这个函数的地址、参数和变量压进栈中。

（3）系统开始执行hanoi（2，x，z，y）函数，if n=1不成立，执行else后的语句为hanoi（1，x，y，z），系统再把函数hanoi（1，x，y，z）的参数和变量值压进栈中。

（4）系统执行hanoi（1，x，y，z）函数内语句，if n=1成立，执行move（x，1，z），此函数执行完毕，返回到调用它的函数处继续执行，并栈中释放此函数参数值。此时，实现了把第1号盘从X塔移到Z塔上。

（5）系统执行move（x，2，y），把握号盘由X塔移到Y塔上，执行完毕后继续执行下一语句hanoi（1，z，x，y），系统进入此函数体内执行，且把参数值压入栈中。

（6）系统执行hanoi（1，z，x，y）函数，if n=1成立，执行move（z，1，x）把1号盘由Z塔移到Y塔上，执行完毕退出此函数，返回调用它的函数处，释放栈中的值。

（7）嵌套调用的hanoi（2，x，z，y）函数也执行完毕，返回调用它的函数执行处继续执行，为move（x，3，z）函数处，并释放栈中的参数值。

（8）执行函数move（x，3，z），把3号盘由X塔移到Z塔上，继续执行下一个语句为函数hanoi（2，y，x，z），把参数压入栈中，开始执行新调用函数。

（9）在hanoi（2，y，x，z）函数中，if n=1不成立，执行else后语句，系统又调用函数hanoi（1，y，z，x），系统把参数压入栈中。

（10）系统执行hanoi（1，y，z，x）函数时，if n=1成立，执行move（x，1，z）把1号盘由Y塔移到X塔上，函数执行完毕，返回调用函数处，执行move（x，2，z），释放栈中参数。

（11）系统开始执行move（x，2，z），即把2号盘由Y塔移到Z塔上，又执行下一个语句hanoi（1，x，y，z），系统把参数值压入栈中。

（12）系统执行hanoi（1，x，y，z）函数，if n=1成立，执行move（x，1，Z）即把1号盘由X塔移到Z塔上，函数返回调用函数处释放栈中参数，函数hanoi（2，y，x，z）执行完毕返回调用处，函数hanoi（3，x，y，z）也执行完毕，返回主函数，并相继释放栈中参数值，栈成为空栈。

至此，主函数程序也执行完毕，实现了把X塔上的3个圆盘借助Y塔移到Z塔上。

3 总结

以上是HANOI塔程序执行过程中，函数调用、栈中内容的变化情况，我认为对于递归问题通过这样的讲解，更能全面理解并掌握其变化过程。设计递归程序时关键要先设计出递归表达式.然后利用分支语句。通过递归调用来实现。递归程序设计的难点是利用降低问题规模的方法设计出递归表达式。本文给出了递归方法的概念、递归方法求解的思路、HANOI塔程序实现过程、，并指出了设计递归程序的思路，为今后编写递归程序及学习计算机语言打下坚实的基础。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。