《巧用思维导图，培养数学预习能力》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

巧用思维导图，培养数学预习能力

范文

刘钟

【摘要】思维导图是一种表达发散性思维的图形工具，通过兼顾图形及文字，能够清楚地将各级主题的关系用层级图表现出来，能够显著增强记忆效果.实践证明，教师在教学环节中利用思维导图引导学生展开预习，能够提高学生的自学能力，起到很好的教学效果.笔者根据多年的教学经验，针对初中数学，浅谈了几点利用思维导图培养学生预习能力的策略.

【关键词】初中数学；思维导图；预习；素养

核心素养是指学生在接受教育过程中，非常需要的必备品格与关键能力，对于他们自身的发展与今后能够更好地适应社会具有重要的意义，它强调的不是知识和技能，而是获取知识的能力.因此，笔者认为，为了深化学生的数学核心素养，教师应当有侧重地培养学生的预习能力，引导他们利用已有的知识经验主动去探究并获得知识，增强创新能力.笔者在教学实践中发现，课堂中巧用思维导图能够有效提高课堂教学效果，引导学生实现高效的自主预习[1].

一、联系旧知，引导自我探索

教师在引导学生进行预习时，应当关注两个要点，一是复习巩固旧知，二是初步感受新知.教师利用思维导图，能够直观形象地联系旧知，从而引导学生利用已有的知识经验对新的内容展开自我探索，提高预习的效率.

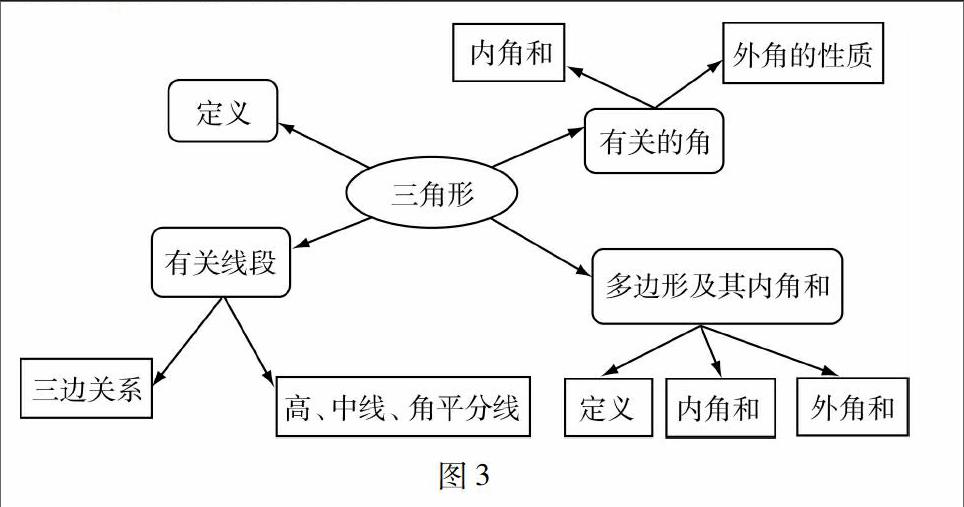
比如，笔者在对“相似三角形”这节内容进行教学时，为了引导学生们类比全等三角形与相似三角形，找到两者的区别与联系，笔者设计了如图1所示的思维导图指导学生对“相似三角形”这部分内容展开了预习.学生们在思维导图的指引下，首先复习了全等三角形的相关内容，例如，全等三角形的定义是指两个完全重合的三角形，两个全等三角形用符号“≌”连接，其性质是对应的边、角、周长、面积、中线、高线、角平分线相等……紧接着学生们在思维导图的指导下开始阅读教材，探索相似三角形的定义、表示方法、性质和判定方法等.通过对比，学生们可以发现相似三角形是全等三角形的拓展与延伸，例如，将三角形全等的判定方法与三角形相似的判定方法进行对比，可以发现：如果两个三角形的三条边对应相等（SSS），则两三角形全等；若三条边对应成比例，则两三角形相似.当然两者也存在一定的区别，全等三角形的判定方法中不存在AAA这一公理，然而若两个三角形的对应角均相等，则两三角形相似.

在上述教学活动中，笔者通过思维导图引导学生们联系旧知对新的内容展开了自我探索，不仅进一步巩固了以往学过的内容，而且促进学生通过新旧知识对比，强化对新知识的理解，高效完成了预习环节的目标.

二、发散思维，拓展广度深度

观察思维导图的结构样式，我们可以发现，思维导图大多是一个中央图向四周发散的形式，反映了多层放射性思考方式，给人的直观感受是具有很强的发散性.学生们在预习时，较强的发散思维能够引导他们更加具有深度、广度地探索知识，起到更好的预习效果.因此，笔者认为，教师应当善于应用思维导图引导学生复习，发散其思维，拓展学生预习的广度深度，提高其预习能力.

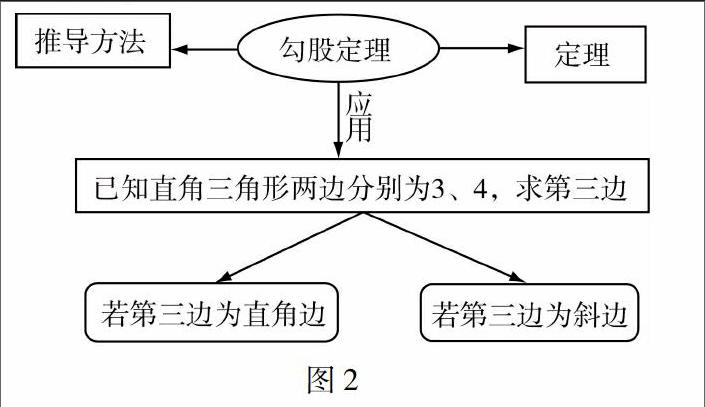
比如，笔者在对“勾股定理”这一节内容进行教学时，通过利用如图2所地的思维导图引导学生对教材进行了预习.学生们在思维导图的引导下，对勾股定理的推导方法、定理和应用等知识进行了学习.其中对勾股定理的应用，笔者在思维导图中列举了一道题，引导学生根据预习的知识对其进行解答.这道问题学生需要分类讨论，因为题目中并没有明确指出所给的两条边是否都为直角边，所以学生需要分别探究第三边为直角边和第三边为斜边这两种情况.通过引导学生多角度的作答，很好地培养了学生的发散性思维，促进他们熟练地掌握勾股定理[2].

在上述教学活动中，笔者通过利用思维导图，引导学生们深入地探索了勾股定理的应用问题，发散他们的思维，使学生们达到了非常好的预习效果.

三、调动内驱，兼顾学生差异

教师除了可以通过自己设计思维导图引导学生达成高效的预习外，还可以通过引导学生自主绘制思维导图，从而激发学生产生预习的兴趣与欲望，调动其内在驱动力.

比如，笔者在对“二次函数”这一节内容进行教学时，首先让学生们自主绘制这一节知识的思维导图，并告诉他們绘制思维导图的方法与技巧：首先选择主要知识点确定为中央主题，然后以此为中心向外作分支，在主分支线上提炼出每一小节的关键词，若关键词下还有更小的分支，则重复上述操作.如果哪一小节自己不理解或有所困惑，可以在关键字附近用彩笔进行标注.笔者发现，学生们在绘制思维导图过程中，兴趣高涨，精神集中，大脑始终处于快速思考的状态.最后笔者一一阅读学生们的思维导图，找到他们的知识盲点，例如，有的学生不会绘制二次函数图像，有的学生不会找二次函数的对称轴……然后兼顾学生的差异，开始进行有针对性的教学.

在上述教学活动中，笔者通过引导学生自主绘制思维导图，激发了学生的积极性与自主性，同时还能发现学生的认知差异，并据此高效开展后续的教学工作.

四、多元整合，升华综合意识

另外，引导学生在预习过程中自制思维导图，还可以升华他们的综合意识.学生们需要通过仔细阅读然后将教材中零散孤立的知识点整合起来，形成一个知识网络，从而对这一章节的知识有一个整体的把握与认识.

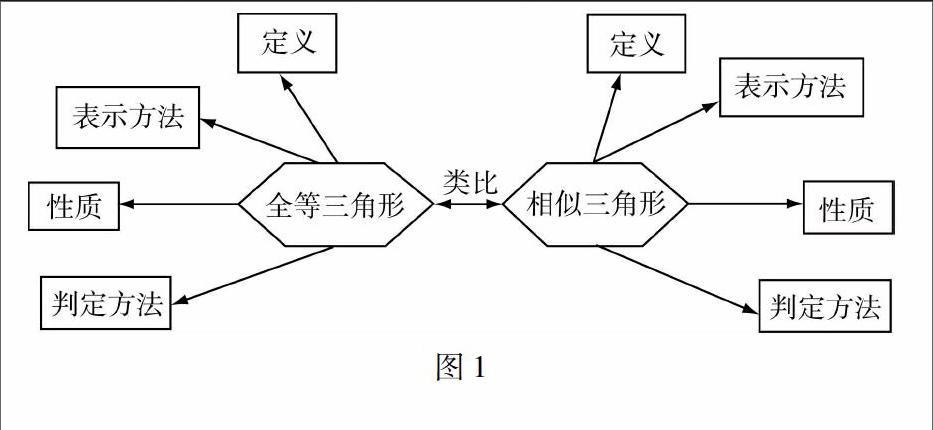
比如，笔者在对“三角形”这一章的内容进行教学时，首先让学生们分组合作共同绘制这一章的思维导图[3].如图3所示，学生们分组制作时，将自己所认为的重点内容都以关键词的形式绘制到思维导图中来，形成了一个知识网络，每一节的内容在其中都有所体现.例如，对于这一章中“与三角形有关的线段”这一节内容，学生们提炼出的关键词为“三边关系”和“高、中线、角平分线”，由此这一节的重点内容显而易见.

在上述教学活动中，笔者通过引导学生在预习教材时绘制思维导图，促进他们将这一章节的全部内容整合到一起，形成一个完整的知识体系，同时提高了学生发现问题、抓住问题本质的能力，升华了他们的综合意识，对其预习能力的提高具有重要的意义.

“凡事预则立，不立则废”，总之，教师在教学过程中通过利用思维导图引导学生联系旧知、发散结构、调动内驱和多元整合，能够有效提高学生的预习能力与自主学习能力，提高他们思维的敏捷性，深化其数学核心素养.

【参考文献】

[1]叶红.基于“思维导图”的初中数学教学设计[J].华夏教师，2015（3）：41.

[2]姜永.思维导图在初中数学教学中的应用分析[J].考试周刊，2014（93）：65.

[3]温英.初中数学教学中思维导图的运用与实践[J].教育，2016（5）：24.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。