《让新知自然生长》-教育论文，中学教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

让新知自然生长

范文

朱华庆

【教学目标】

1.理解二元一次方程、二元一次方程组及其解的概念。

2.会用已有知识探究二元一次方程及方程组的解法。

3.感知单元知识架构，体会问题到数学再回到问题的建模思想。

4.培养探究问题的习惯、能力，体会重要的数学思想。

【难点】探究方程的解;会用数学方法来探究实际问题。

【重点】类比概念、单元知识结构来探究问题。

【教学流程】

一、复习旧知，搭建框架

师：我们刚学完了一元一次方程，都学习了哪些知识？

生：学了什么是一元一次方程。师：也就是一元一次方程的概念。

师：一元一次方程的概念是什么？（师生互动，点出元和次的意义。）

师：学习了一元一次方程的概念后还学习了哪些知识？

生：一元一次方程的解，一元一次方程的解法，一元一次方程的应用。

这个环节重在回顾一元一次方程单元结构，对重点知识进行唤醒，为后续学习作铺垫。

二、类比旧知，激活新知

师：下面请同学们用所学的知识来解决实际问题（PPT呈现问题）：小明到商店买文具，若买3支铅笔和2本笔记本，需花费7元;若买2支铅笔和4本笔记本，需花费10元。求铅笔和笔记本的单价分别是多少元？

（学生用一元一次方程解决问题，教师板书规范过程。）

师：用一元一次方程解决刚才的问题，难点在哪里？

生：表示笔记本的单价7-3x/2比较难想到。

师：能否找到合适的数学方法化解这个难点？

生：直接设笔记本的单价为y元。

师：为什么？

生：这样表示笔记本的单价更加简单，更

容易想到。师：你还能根据等量关系列出等式吗？

（学生经过尝试后，列出两个方程，教师板书。）

师：你们认为这两个方程应该怎么命名？为什么？

生：二元一次方程，因为它含有两个未知数，含有未知数的项的次数是一次。

师：这就是我们今天要学习的二元一次方程。这两种方法你们选哪一种？为什么？

生1：选第二种，容易想到，而且列方程比较简单。

生2：我选第一种，因为第一种可以算出来，第二种不会算。

（以此为切入点，引导学生探究二元一次方程。）

师：你认为什么是二元一次方程？

生1：含有两个未知数，含有未知数的项的次数是一次的方程就是二元一次方程。

生2：还必須是整式方程。

师：xy=1是二元一次方程吗？

生1：是的，符合上面3个条件。

生2：不是，xy是2次。

师：xx=1是什么方程？是一元一次方程吗？

生：不是，因为xx=1就是x2=1，未知数x是2次了。

师：那么xy=1是二元一次方程吗？

生：不是。

师：怎么修改？

（帮助学生提炼、完善概念;PPT呈现二元一次方程辨析题。）

师：了解了二元一次方程的概念，我们下一步研究什么内容？

生：方程的解。师：什么是二元一次方程的解？生：使方程两边的值相等的未知数的值。师：你能求出二元一次方程的解吗？说一说

你怎么求的？（PPT呈现：用列表找二元一次方程2x+4y=10的解。）

师：两种方程的解有何不同之处？（PPT呈现表格：一元一次方程与二元一次方程解的对比。）通过这个环节，学生初步感知探究方程的基本思路、方法，同时，新问题的出现为下面活

动找到了探究的切入点。

三、探究新知，感知方法

师：为什么二元一次方程的解是无数组？

生：两个未知数，一个变化了，另一个也会发生改变。

师：我们发现1个二元一次方程是无法求出唯一解的，怎么办？

生：要两个二元一次方程。

师：这就是即将要学习的二元一次方程组。我们可以从哪些方面探究二元一次方程组？

生：概念、方程组的解、解方程组、应用。

师：什么是二元一次方程组？

生1：含有两个未知数，未知数的项的次数是一次的整式方程。

生2：两个二元一次方程构成方程组。

（教师引导学生完善二元一次方程组的概念，通过PPT对概念加强理解。）

师：在了解了二元一次方程组的概念后，接下来探究什么？

生：二元一次方程组的解。

师：什么是二元一次方程组的解？生：使方程成立的未知数的值。

师：使哪个方程成立的未知数的值，为什么？

生：使两个方程都成立的未知数的值。

师：这两个方程中，x、y值是否相等？为什么？

生：相等。因为它们代表的含义相同，x表示铅笔的单价，y表示笔记本的单价。

师：所以，未知数的值必须同时满足两个方程才是方程组的解。为了表达这两个方程之间的关联性，我们必须在两个方程前面加一个大括号，方程的解也必须有大括号，因为它们是有关联的。（教师出示PPT，让学生用列表法找方程组的解。）

这个环节主要是了解方程组的概念，会通过列表找到方程组的解，理解方程组解的关联性。

四、探究解法，认知本质

师：刚才是怎么找到方程组的解的？

生：找两个方程相同的解，就是方程组的解。

师：这种求方程组的解的方法有什么缺陷？

生：如果数据较大，或者解是小数，通过列表找解就比较困难了。

师：是否可以从数学运算的角度来探究，把方程组的解算出来？

生：可以，买3支铅笔和2本笔记本，需花费7元，那么买6支铅笔和4本笔记本就是14元，而买2支铅笔和4本笔记本，需花费10元，所以4支铅笔就是4元，所以铅笔每支1元，然后笔记本就是2元一本。

师：能否用数学符号把等式表示出来。

生：可以，将3x+2y=7表示为1式，将6x+4y=14表示为3式，将2x+4y=10表示为2式。

师：刚才的等式对你解方程组有何启发？

（通过对三个等式的对比分析，初步了解方程组解法的本质;教师板书解方程组的规范过程，告知学生加减消元法的由来。）

师：还有其他方法吗？刚才我们是怎么解的？关键的突破在哪里？生：3-2的时候y没有了。师：这时变成了什么方程？

生：一元一次方程。

师：黑板上2x+4×7-3x=10，会解吗？

生：会。

师：与2x+4y=10对比一下，解这个二元一次方程的困难是什么？

生：因为它有两个未知数。

师：能否把两个未知数转化为一个未知数？

师：我们之前把7-3x看成一个整体，得到2了二元一次方程，如果反过来想呢？7-3x

生：把y看成2。

师：也就是y=7-3x2，对不对？是否相等？

生：根据题目中的数量关系可以得到。

师：能否从数学运算的角度得到？例如二元一次方程3x+2y=7有什么用？

7-3x生：可以化简得到y=2。

（师生共同板书解方程组的规范过程。）师：这个解法叫代入消元法。所以解二元一次方程组的关键是什么？

生：把二元化为一元。

师：怎么转化？（进一步引导学生感知解二元一次方程组的本质——消元。）这个环节主要是探究二元一次方程组的解法，让学生理解解法的本质。

五、课堂总结，感悟提升

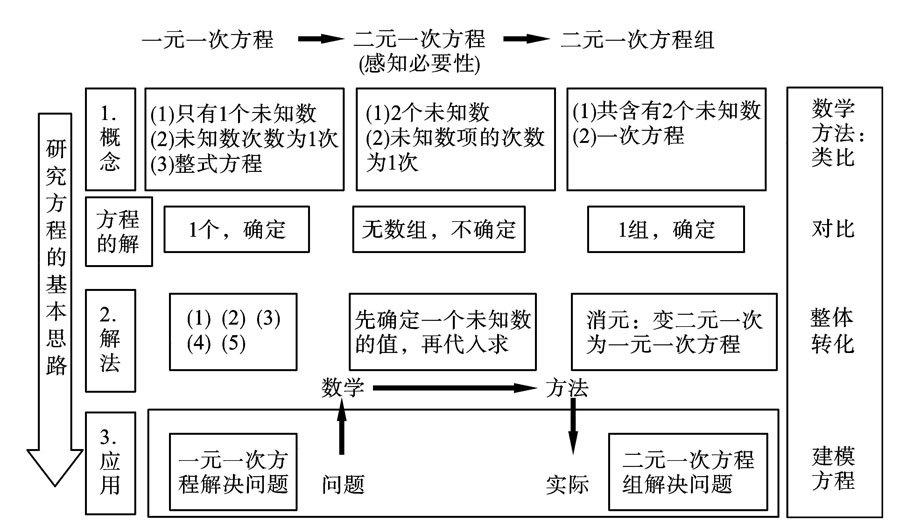
师：这节课同学们有哪些收獲？（PPT呈现结构图。）

生：知道了研究二元一次方程组的一般过程——概念，方程的解，解法，应用。

师：本节课还有哪些是你印象最深刻的地方？

生1：研究问题的方法，类比思想、转化思想，把二元一次方程转化为一元一次方程。

生2：二元一次方程组的解法。

师：同学们说得都很好。本节课我们通过学习整章的内容，了解了学习二元一次方程组的必要性，也知道了研究方程的一般思路，更学到了研究数学的方法：类比，转化，方程思想等。如果到九年级学习一元二次方程呢？甚至是三元一次方程，你会研究吗？

（对本节课的重要的内容、思想方法予以总结，为以后学习埋下伏笔。）

【教学反思】

李尚志教授说过，一条重要的核心素养是举一反三的能力，就是能利用旧知识解决新问题的能力，层次更高一点，就是利用旧知识生长新知识的能力。

通过本节课的学习，学生体会从整体认知的角度来看待问题，从类比旧知识中感知新知，在探究解法的过程中运用转化思想，感知数学问题的本质，从而为探究问题积累方法、经验。

就本节单元课而言，应该处理好如下几个问题：

学生层面：1.学二元一次方程组的必要性（为什么学）;2.探究方程的一般思路（怎么学）;3.感知数学与问题的建模思想（有什么用）。

教师层面：明暗两条线路推进。1.探究的方程思路（明线）。问题的引入（学习的必要性、兴趣点）→概念的形成、理解（类比旧知激活新知）→解法的探究（探究的切入点）→解法的选择与总结→解决问题。

2.对单元课“整体感知”的设计（暗线）。

（1）了解研究实际问题的思路：实际问题→抽象为数学问题→提炼出数学方法→实际问题。感知数学知识生长的必要性。

（2）理解探究方程的思路：概念的发现→概念类比→概念的提出→概念的深化，解法的提出→解法的类比→解法的猜想→解法的提炼。感知数学概念、方法生长的合理性。

当然，一节好课的标准有很多，除了课堂的设计之外，首先要更多关注学生的成长，例如对于探究的兴趣和习惯的培养，课堂上最后对三元一次方程的提问，会带给学生很多遐想;其次要关注学生的学情，不同的学情在上单元起始课时有较大的出入，特别是在教师引导和学生互动方面以及学生能否真正感悟到本节课的真谛，大为不同。

（作者单位：江苏省常州市金坛区尧塘中学）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。