《提升直观想象素养引领学生学习函数》-理学论文，中学数理化论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

提升直观想象素养引领学生学习函数

范文

曹颖慧

[摘要]函数是中学数学中最重要的概念之一由于函数在中学数学中的核心地位与自身的抽象性、复杂性，导致它是高一新生面临的第一个“瓶颈”提升学生直观想象素养，可以让学生更好地理解函数

[关键词]直观想象素养;函数;中学数学

[中图分类号]G633.6

[文献标识码] A

[文章编号] 1674-6058（2020）17-0019-03

函数是中学数学中最重要的概念之一.由于函数在中学数学中的核心地位与自身的抽象性、复杂性以及初高中教材内容、学习方法、教学方法、认知水平的差异，导致它是高一新生面臨的第一个“瓶颈”.这就要求教师将比较抽象的学术形态内容转化为学生容易直观感知的教育形态内容.

教师在函数教学中，借助函数图像的直观性，可使得抽象问题变得具体、形象，从而使学生对函数的认识更清晰、更深刻，有助于学生理解函数的本质.下面分三个方面说明如何提升学生直观想象素养，引领学生度过函数学习难关.

一、概念性知识教学

每个概念的形成，都可以采用“创设情境一形成概念一深化理解”这样一种教学流程，引导学生充分经历概念的建构过程.

[案例一]偶函数概念教学.

1.创设情境

给出两个函数f（x）=X2和g（x）=2-|x|的图像，思考并讨论以下问题：

（1）这两个函数图像有什么共同特征？

（学生很容易看出两个函数图像都关于y轴对称）

（2）相应的两个函数对应表是如何体现这些特征的？请学生填写下列表格.

学生观察到f（-l）=f（1）、f（-2）=f（2）、f（-3）=f（3）;g（-1）=g（1）、g（-2）=g（2）、g（-3）=g（3）.

（3）在计算机上作出函数f（x）=x2的图像，如图3.在图像上任取一点A，作出点A关于y轴对称的点B，发现点B也在函数的图像上.测出点A和点B的坐标，得到横坐标互为相反数，纵坐标相等.令点A在图像上移动，点B随之移动，依然是A、B两点横坐标互为相反数，纵坐标相等.

2.形成概念

函数f（x）=x2和g（x）=2-|x|对于R内任意的一个x，都有f（-x）=（-x）2=x2=f（x）、g（-x）=2-|-x|=2-|x|= g（x），这时我们称函数f（x）=X2和g（x）=2-|x|为偶函数.由此我们抽象出偶函数的概念：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），那么函数f（x）就叫作偶函数.

3.深化理解

①请同学们判断下列两个函数是不是偶函数并作出图像.经判断，f（x）和g（x）都是偶函数，图像如图4、图5.

②已知f（x）是偶函数，试将图6补充完整.

在概念性知识教学时，一般是先从几何直观（观察图像）人手，然后运用自然语言描述函数的图像特征，最后抽象到用数学符号刻画相应的数量特征.

二、综合函数的研究性教学

[案例二]探究函数f（x）=x+1/x

（I）你认为可以从哪些方面研究这个函数？

（Ⅱ）你认为可以按照怎样的路径研究这个函数？

（Ⅲ）按照你构思的路径研究你想到的问题.

分析：（I）我们研究函数通常要研究下列几个方面：图像、定义域、值域、单调性、奇偶性等.

（Ⅱ）研究路径：

①求定义域，以确定函数图像在礴由上的取值范围;

②判断奇偶性，以确定函数图像是否具有对称性;

③y=x和y=1/x是两个幂函数，在同一坐标系中作出两个函数的图像，分析两个函数的增长或衰减速度，判断函数f（x）=x+1/x的单调性;

④用定义证明单调性的判断是否正确;

⑤根据定义域、奇偶性、单调性作出函数f（x）=x+1/x的图像草图;

⑥利用草图确定函数的值域;

⑦在计算机上作出函数f（x）=x+1/x的图像验证以上分析.

（Ⅲ）研究问题：

单调性、奇偶性与函数图像有密切关系.了解了函数的单调性，基本上就可以决定函数图像的走势;反过来，掌握了函数图像的走势，也就基本上了解了函数的单调性.如果函数有奇偶性，那么只需要研究x>0的部分，利用对称性我们就知道x<0部分的性质.

三、函数模型的应用课教学

[案例三]假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下.

方案一：每天回报40元;

方案二：第一天回报10元，以后每天比前一天多回报10元;

方案三：第一天回报0.4元，以后每天的回报比前一天翻一番.

请问，你会选择哪种投资方案？

分析：设第x天所得回报是y元，则方案一可以用函数y=40x（x∈N*）进行描述;方案二可以用函数y=10x（x∈N*）进行描述;方案三可以用函数y=0.4×2x-1（x∈N*）进行描述.三个模型中，第一个是常数函数，后两个都是增函数.要对三个方案做出选择，就要对它们的增长情况进行分析.

在同一坐标系中作出三个函数的图像，如图9，方案一的函数是常数函数，方案二、方案三的函数都是增函数，但方案三的函数与方案二的函数的增长情况很不相同.方案一和方案二增长量固定不变，而方案三是“指数增长”，其“增长量”是成倍增加的，从第7天开始，方案三比其他两个方案增长得快得多.

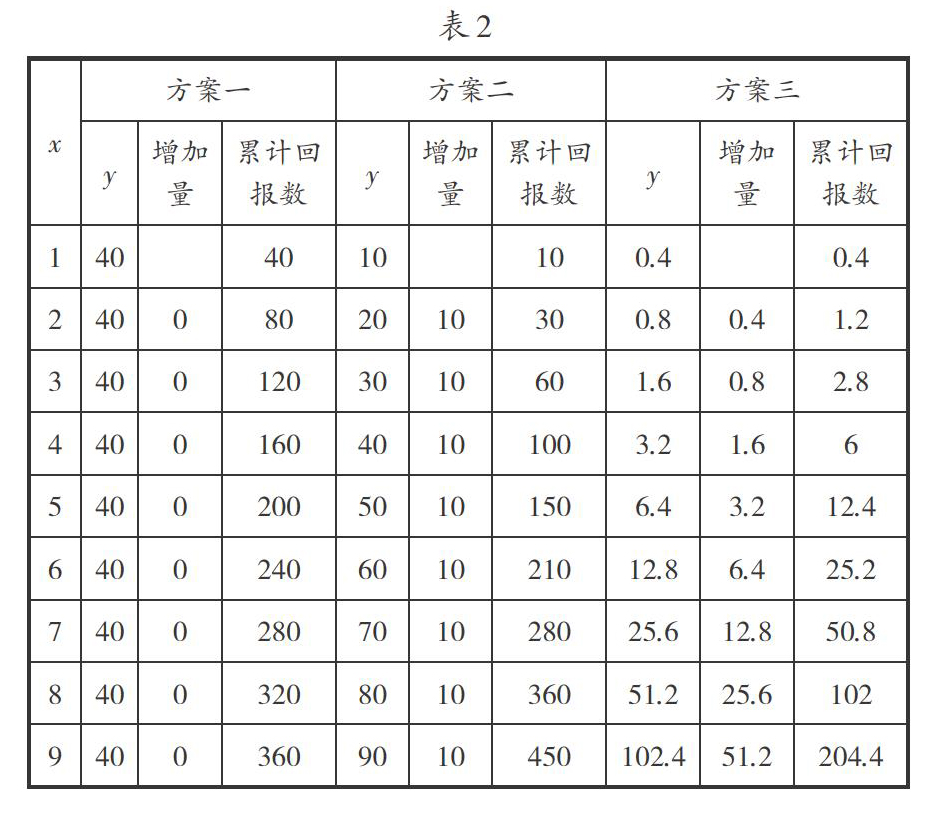
学生填写相关表格（表格形式略），计算出三个方案每天的回报数v、增长量和累计回报数.然后教师用EXCEL软件快速填好表格（如表2）.

因此，投资1-6天，应选择方案一;投资7天，应选择方案一或方案二;投资8-10天，应选择方案二;投资11天（含11天）以上，则应选择方案三.

函数关系是平面上点的集合，又可以看成平面上的一个“图形”，在很多情况下，函数是满足一定条件的曲线.因此，从某种意义上说，研究函数就是研究曲线的性质，研究曲线的变化.在讨论函数问题时，应帮助学生养成画函数图像、用函数图像思考问题的习惯.树立“图形意识”是掌握函数性质、学好函数的关键.

[参考文献]

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S]北京：人民教育出版社，2018.

[2]史宁中，王尚志普通高中数学课程标准（2017年版）解读[M]北京：高等教育出版社，2018.

（责任编辑黄桂坚）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。