《基于GARCH模型的波罗的海干散货运价指数预测》-工学论文，水运论文-论文范文参考-科学狗论文网

标题

基于GARCH模型的波罗的海干散货运价指数预测

范文

沙蔚婷

【摘要】研究波罗的海干散货运价指数（BDI），对其日收益率序列建立模型，并比较不同分布的各模型优劣。结果表明，基于不同分布的GARCH模型对BDI的静态预测误差均很小，利用GARCH模型对短期运价波动的预测精度较高。

【关键词】波罗的海干散货运价指数（BDI）；GARCH模型；静态预测

1985年，波罗的海航运交易所发布日运价指数（BFI）。该指数是由若干条传统的干散货船航线的运价按照一定的权重构成的综合性指数。1999年9月1日，波罗的海交易所发布了波罗的海巴拿马型指数（BPI）和波罗的海海岬型指数（BCI）。同年11月1日，在BCI，BPI和波罗的海大灵便型指数（BHI）等三大船型运价指数的基础上发布了波罗的海干散货运价指数（BDI），取代了BFI，成为了国际干散货运输市场走势的晴雨表。

1 国际干散货运输市场运价走势

21世纪初，我国的经济建设带动了原材料的需求增长，推动了干散货运输市场的繁荣发展。2003年，BDI低于点，而到了2004年，该指数翻了一番，达到点以上。我国对全球初级原材料的旺盛需求，推动了国际干散货海上运输价格上涨。海运价格与大宗原料价格具有相似的变化趋势。

干散货运输市场的转折点出现在2008年。在2008年之前，国际干散货运输市场形势良好，BDI曾经突破点。2008年5月7日至2008年6月12日的1个多月内，BDI均保持在点之上；5月20日，BDI达到历史最高点，为点。然而，到了下半年BDI连跌不止，于年底跌至700点左右。造成运价下跌的主要原因是运力过剩。2007年美国发生了次贷危机，之后演变成为全球金融危机，导致全球经济衰退，运输需求减少。

宏观经济的突变对干散货航运市场造成了长远的影响，使货源与运力之间的不平衡现象长期存在。2009年至2010年，国际干散货运输市场缺乏货源，运价始终处于较低水平。得益于铁矿石和煤炭货种的带动，干散货航运市场整体恢复情况较好，BDI基本保持在点以上，部分航运企业依旧盈利。2009年，BDI均值点，同比降低了59%；2010年，BDI止跌企稳，均值为点，同比上涨了5.4%。

2011年，欧债危机爆发，各国经济衰退。2011年，BDI均值跌至点；2012年，BDI均值为920点。在国际干散货运输市场中，众多航运企业巨额亏损，在干散货货运量以及货运周转量方面出现了大幅的减少。

国际干散货运输市场低迷的原因主要在于市场运力供给过剩。在干散货运输市场繁荣时，航运企业过于乐观地预估市场，通过购买新船或者租入二手船来扩大船队规模，赚取更多利润。但是，由于航运市场突变，货源大幅减少，航运企业扩张运力的决策加剧了供需失衡。伴随着干散货运价的下跌，租船费率也随之下跌，但航运企业仍需要按在租船合同签订时约定的高额费率支付租金，以目前的运价根本无法承受如此高的成本，这进一步加重了航运企业的损失。

2013年，BDI总体较上年同期有所回升，均值为点，同比增长31%。以BDI计算，新船投入运营的盈亏平衡点在～点，旧船盈亏平衡点约为点，平均盈亏平衡点在点左右。可见，2013年大部分干散货航运企业仍旧入不敷出。

2 BDI日收益率序列的GARCH 模型建立

2.1 方法

广义自回归条件异方差模型（GARCH模型）通常用于对回归和自回归模型的随机扰动项进行建模。该模型对误差的方差进行了进一步的建模，尤其适用于波动性的分析和预测。因此，本文利用GARCH模型对BDI进行分析。

2.2 数据的选取和处理

选取2008年9月22日至2012年9月25日的BDI交易日数据，共计个，作为建立模型的样本；以2012年9月26日至2013年2月20日的数据为样本外数据，共计100个，用于预测（数据来源：克拉克森航运咨询网）。

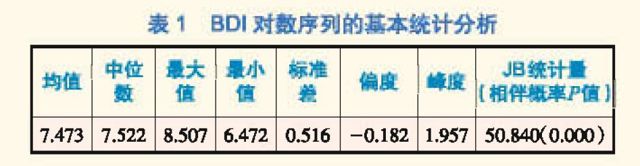
对BDI序列进行自然对数处理，BDI对数序列的基本统计分析结果见表1。

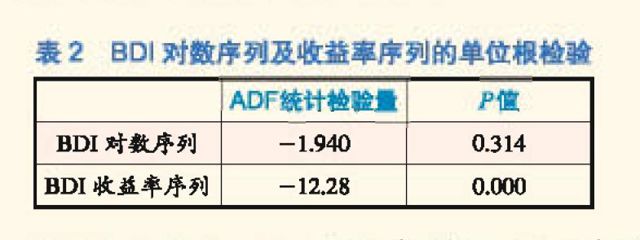
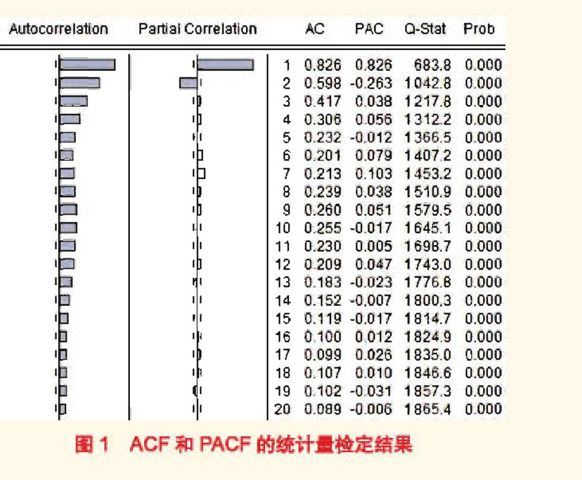
2.3 平稳性及自相关性检验

2.4 异方差检验及GARCH模型建立

利用拉格朗日乘子检验残差序列是否存在ARCH效应。ARCH检验的第2行是obs*R-squared值（LM统计量）以及检验的相伴概率（见图2）；在落后期数q=10的情况下，LM统计量为（P=0.000），小于显著性水平0.01，可以在至少99%的置信水平下拒绝原假设。由此说明，残差不仅存在ARCH效应，而且存在高阶ARCH效应。因此，利用GARCH模型对残差序列建模，提取残差中的信息，使模型残差项成为白噪声。

对残差 t 是否服从正态分布进行检验，基本检验结果见表3。

在表3中：残差分布峰度值大于3，具有尖峰厚尾特征；JB统计量达到，P值为0.000，小于0.1，显示残差分布不服从正态分布。因此，分别建立残差 t基于正态分布和t分布的GARCH模型，并比较在不同分布下模型的优劣。[1]

综合运用AIC准则（赤池信息量准则）和SC准则（施瓦兹准则），在滞后项不超过2的情况下逐个检验，选择AIC和SC数值最小的GARCH（1，1）模型（见表4）。利用GARCH（1，1）模型对BDI收益率序列的残差序列进行建模。

以正态分布和t分布为基础分布的GARCH（1，1）模型均满足宽平稳条件。由GARCH（1，1）模型估计结果可以看出，在正态分布中，a（B） + （B）=0.357 569 + 0.415 721<1；在t分布中a （B） + （B）=0.448 967 + 0.511 666<1。参数全部通过显著性检验，标准化残差及其平方项的Ljung-Box统计量均不显著，说明残差序列不存在自相关性，GARCH效应已经消除。比较在不同分布下模型的优劣，t分布具有更小的AIC值和更大的ln L值（对数似然比），说明t分布比正态分布更能反映BDI收益率序列的尖峰厚尾性；在t分布GARCH（1，1）模型中，a（B） + （B）非常接近于1，说明BDI具有波动集聚效应，波动的持续时间较长。

3 预测误差比较

以2012年9月26日至2013年2月20日的数据为样本外数据，通过样本内数据所建立的AR（2）-GARCH（1，1）模型，对样本外数据进行静态预测。静态预测中的被解释变量总是采用滞后变量的实际值而不是预测值来计算向前一步的结果。本文使用平均误差百分比（MAPE）作为误差衡量标准，MAPE的计算公式为

在不同分布下，模型的预测误差均小于2%（见表6），说明各种预测方法的误差都很小。样本外预测误差大于样本内预测，这是由于样本外预测的参数来自于样本内而导致的结果。不论样本内外，在t分布的假设下，模型的预测误差都更小。

4 结语

实证结果表明，BDI是可以预测的。BDI的形成受即期滞后变量的影响较大，而BDI收益率序列具有高阶ARCH效应，基于t分布的GARCH模型能够更好地消除残差序列的异方差性，且体现出明显的波动集聚效应。基于不同分布的GARCH模型对波罗的海干散货运价指数的静态预测误差都小于2%，说明短期预测效果很好。

参考文献：

[1] 翟海杰，李序颖.不同分布的GARCH族模型的波罗的海干散货运价指数波动率[J].上海海事大学学报，2009，30（3）：59-64.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。