《基于Open CASCADE的曲面法线方向计算》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于Open CASCADE的曲面法线方向计算

范文

李都宁毛力奋原力王普勇蒋光南

摘要：法线方向是曲面的重要参数，在计算图形学中被广泛使用，如场景中的光照及阴影效果、法线贴图效果、三维网格生成等，准确计算得到曲面上某点的法线对各类图形效果处理的质量具有重要的意义。本文利用Open CASCADE图形库，对其中的曲面几何对象的法线方向计算方法进行了分析，提出计算曲面法线方向的稳健性方法，并对比了不同计算方法所得到的法线对网格划分产生的效果，验证了曲面法线方向计算过程的有效性。

关键词：Open CASCADE;曲面法线;BREP

中图分类号：TP393? ? ? ? 文献标识码：A

文章编号：1009-3044（2019）23-0287-04

开放科学（资源服务）标识码（OSID）：

Open CASCADE（Open Computer Aided Software for Computer Aided Design and Engineering）是由法国Matra Datavision公司开发的CAD软件系统，是世界上最重要的开源几何造型基础软件平台，它的存在大大方便了各类科研组织进行相关的图形学研究。该图形库是基于OpenGL开发的专用CAD类库，提供了CAD模型建模与操作、CAD模型格式读取与保存等功能，广泛应用于CAD软件开发、CAE仿真软件设计等方面。

曲面上某点的法线方向指的是在该点处与表面垂直的方向，对于平面来说，平面上各点的法向是一样的，对于曲面来说，各点的法线方向则并不相同。法线方向作为曲面的重要属性，在图形学领域中被大量使用[1]，其正确性对图形场景中的光照、阴影效果、贴图效果等有直接影响。将曲面的法线信息应用于CAE软件网格划分过程中，能够改善划分网格的质量。

通常情况下曲面法线计算有两种方式，一种是微分法，通过曲面数学方程计算[2]。另一种是平均邻接面法，通过曲面的离散化三角形计算。第二类方法最早由Gouraud[3]提出，采用顶点所在面的法线代表顶点法线，Max[4]提出了采用加权的方式处理顶点法线。在国内，孙娟[5]使用SVD方法计算了曲面上顶点的法线，程磊[6]则提出了棱边分裂法，改进了棱边位置处顶点法线的计算精确度。

本文对Open CASCADE曲面法向方向的计算方法进行分析，采用传统微分几何法、离散三角面片平均法与Open CASCADE中曲面属性相结合的新方法，从而提高了Open CASCADE曲面法线计算的精确度。

1 Open CASCADE曲面

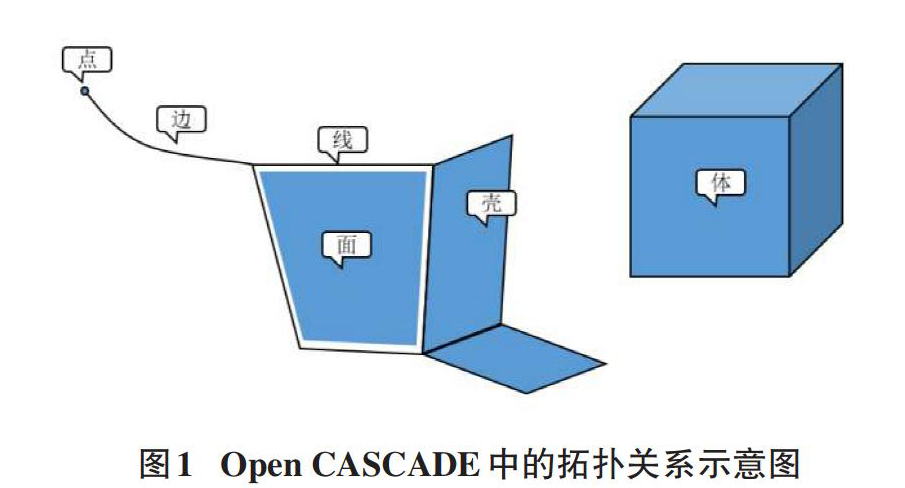
Open CASCADE中采用边界表达法（Boundary Representation，简称Brep）来表示曲面，该方法根据顶点、边和面构成的曲面来精确地描述三维模型，描述信息主要包括几何（Geometry）和拓扑（Topology）两部分。一般来说，几何信息对几何对象的形状、大小、位置等进行描述，如面的形状、点的坐标，拓扑信息对几何上的顶点、边、面的拓扑连接关系进行描述，如图1所示。几何信息依附于拓朴信息而存在的，在Open CASCADE中，TopoDS拓扑类实现了BRep几何模型。

曲面（Face）是Open CASCADE中用来描述三维实体边界的拓朴，由曲面的几何及若干个曲线（Wire）来描述。以圆柱体为例，圆柱体包含三个面：底面、顶面和侧面。底面和顶面属于Geom_Plane几何类型，侧面属于Geom_CylindricalSurface几何类型，通过顶面和底面的曲线来限定面的边界，从而得到实际的圆柱面。三维模型空间中的曲面一般采用二维参数空间{u， v}来进行定义，参数区间可以有界或无界，如对于圆柱侧面Geom_CylindricalSurface类型的曲面，其u方向区间为[0，2π]，v方向区间为（-[∞]，+[∞]）。三维曲面空间和二维参数空间的映射关系示意图如图2所示。

在计算机中对曲面进行显示时，通常会对曲面进行三角剖分，得到离散的三角面片数据，对三角面片增加材质、光照等渲染效果后，即可较好的在计算机屏幕上显示出三维的曲面模型，在OpenCASCADE中曲面剖分后的三角面片数据是保存在曲面的数据结构中。一般情况下，可以在参数空间上进行网格剖分，然后再映射到三维模型空间，如图3所示。在求曲面上某点的法线方向时，所求的点位置通常指三角面片的顶点位置。

2 法线计算方法

Open CASCADE中曲面采用数学参数方程来描述，是曲面的精确表示，因此可以通过求微分的方法得到曲面上的切向向量，然后由两个切向向量的叉乘得到曲面的法向量。图4中曲面S（u，v）上点P对应的一次微分Su，Sv即为曲面在该点处的切向量。

点P处的法向量N可用式（1）计算得到。

N = Su? Sv? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

曲面离散为多个相连的三角形后，每個顶点同时位于几个不同的三角形边界上，因此可将与该顶点相邻的三角形法向量进行平均得到该顶点的法线，其中每个三角形的法向量可根据三角形两条边矢量的叉积计算得到。如图5所示，曲面顶点P的法向就等于其相邻六个三角形的法向平均值。为了得到更加准确的法线向量，可采取不同的平均方式对三角形法线向量进行处理，例如，可以使用每个三角形的面积作为加权的权值。

3 Open CASCADE曲面法线计算

Open CASCADE中的曲面是用参数方程来表示的，同时在曲面的数据结构中也保留有三角网格数据。为了得到更加精确的曲面法线，首先可以基于曲面参数方程，采用微分法来直接计算法向量，如果该方式计算失败，则采用平均法向的方法来计算。

实际中基于曲面参数方程法计算法线之所以会失败，是因为采用参数形式时，需要处理由参数化引起的奇异性（Singularity）。这种奇异性是由于参数方程引起的，典型的例子是参数表示的球面，Open CASCADE中球面的参数方程如式（2）所示。

[Su，v=P+r?cosv?cosu?Dx+sinu?Dy+r?sinv ?Dz] （2）

其中，[u，v∈0，2π×[-π2，π2]]。当[v=-π2]时，对于任意的[u∈0，2π]有：

[Su，-π2=P-r?sinv ?Dz] （3）

从式（3）中可以看出，[v=-π2]时所对应的参数空间中的边退化（Degenerated）成了一个点，即球面的极点。同样的，当[v=π2] 时也存在边的退化情况。

对于球面来说，显然极点处的法线是存在的，然而对于式（3）所表示的参数方程，则无法通过切向量叉乘的方式计算法向量。事实上，通过球面的参数方程可以计算得到某点u、v方向上的切向量如式（4）、（5）所示。

[Su=r?cosv?（-sinu ?Dx+cosu ?Dy）] （4）

[Sv=-r?sinv?cosu ?Dx+sinu ?Dy+r?cosv?Dz] （5）

当[v=-π2]或[π2] 时，对于任意的[u∈0，2π]有：

[Suu，-π2=Suu，π2=0] （6）

即在球面的极点处切向量[Su]为零向量，这就意味着不能通过对切向量叉乘的方式计算法向量。由此可知，对于参数化的曲面，需要u或v方向上的切向量均不为零，才能求出法向量。

Open CASCADE中对退化点的法线计算采用近似的方式进行处理。首先，用一阶泰勒展开代替法线向量N（u，v），则计算法线方向等效于求曲面上某点处的二阶微分，如果计算仍旧没有成功，则给定退化点附近微小的步长，计算距离退化点微小距离的点的法向量。由上可知，退化点处的法线会出现计算不准的情况。

实际上，Open CASCADE中对于不同的曲面类型，提供了很多额外的几何信息，可以充分利用Open CASCADE几何的属性来判断并计算特殊点处的法线方向。以圆锥为例，对于圆锥曲面上的点，只有圆锥顶点的位置比较特殊无法计算得到，其他位置的法线可以通过微分法得到。Open CASCADE中对圆锥曲面定义了主轴方向属性，如图6所示。

其中，如果圆锥半锥角为正的话，锥尖在主轴的负方向，半锥角为负的话，锥尖在主轴的正方向。因此，可以借助圆锥曲面半锥角的正负以及主轴方向来定义圆锥顶点的法线方向，从而得到准确的结果。

综上，对于Open CASCADE中的曲面S，求曲面S上点P（P为曲面离散三角形面片上的某个顶点）的法线，相应的算法流程为：

a）判断曲面S类型及点P的位置，如果为存在奇异点的曲面（如圆锥曲面），且点的位置是奇异点，转步骤b），否则转步骤c）;

b）根据曲面信息中的参数，计算奇异点P的准确法线，转步骤g）;

c）求点P处u，v方向上的切向量，如果切向量存在为零的情况，转步骤d），否则转步骤e）;

d）求点P处的二阶微分，通过一阶泰勒展开近似计算法线方向，判断法线方向是否正确（非零向量），正确转步骤g），否则转步骤f）;

e）通过切向量叉乘得到法线方向，转步骤g）;

f）将P点所相连的三角面片法线进行平均，作为P点法线方向，转步骤g）;

g）输出法线方向。

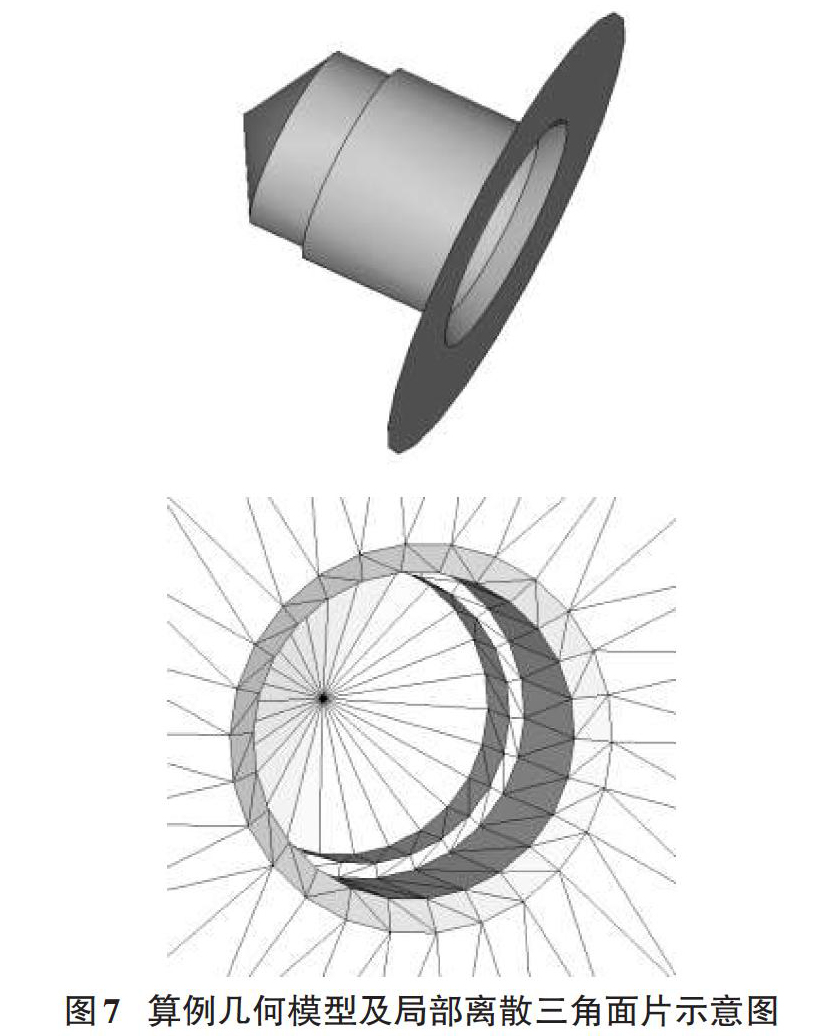
为了验证上述算法流程的有效性，这里以一个包含圆锥曲面的几何模型为例，采用不同方法计算得到相应的曲面法线，然后使用法线信息进行网格生成，并对比所生成网格的效果。算例几何模型以及其局部的三角面片模型如图7所示。

网格划分要求对离散模型中所有三角形的每个节点位置计算法线方向，理论上同一个位置的节点法线方向在每个三角形中计算的结果均相同，但实际中由于计算方法的不同，确会出现不同的结果。这里分为三种情况进行对比：

1）曲面奇异点采用求二阶微分的方法处理，若求解不成功，则计算离奇异点非常近的点法线方向;

2）曲面奇异点采用三角面片法线平均的方法处理;

3）曲面奇异点采用本文提出的算法流程处理。

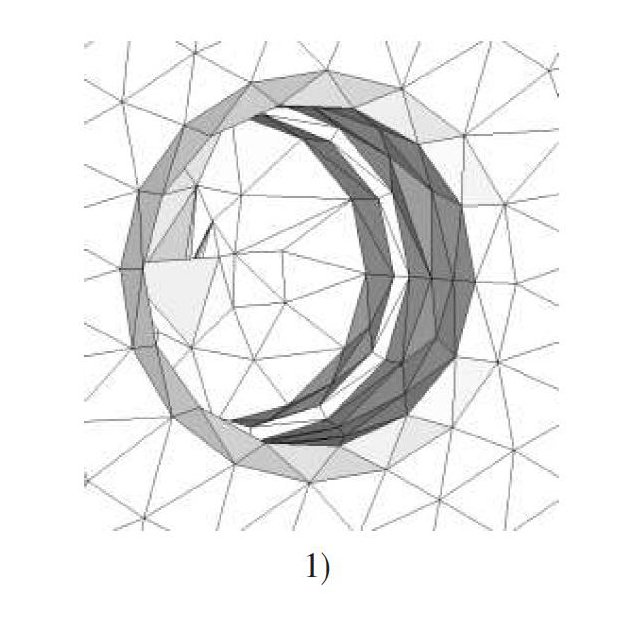
根据不同算法得到的法线方向划分得到的网格如图8所示。

由图8可以看出，第一种情况下，由于采用微分法计算法线，在不同三角形中的奇异点处计算得到的法线方向很可能不一致，导致在圆锥顶点处的网格生成错误。第二种情况下，采用离散三角形法线平均的方式得到的法线方向一致，但存在一定的方向偏差，在划分网格时会判断此处法线方向变化较大，从而加密网格。第三种情况下，得到的法线方向一致且无偏差，划分的网格比较均匀。

4 结论

本文基于Open CASCADE的曲面提出了一种计算法线方向的方法，该方法有效结合了微分法、平均法线法以及曲面的属性信息，通过实际网格划分的验证，表明该方法具有适应性强的特点，能够精确的获取到曲面法线方向。

参考文献：

[1] 张云苑. 3D游戏中法线贴图技术的数学方法[J]. 电脑知识与技术， 2011， 7（32）.

[2] Gouraud， H. Continuous Shading of Curved Surfaces[J]. IEEE Transactions on Computers， 1971， C-20（6）：623-629.

[3] Max， Nelson L.. Weights for Computing Vertex Normals from Facet Normals[J]. Journal of Graphics， GPU， & Game Tools， 1999， 4 （2）： 1-6.

[4] 孫娟. 使用SVD计算顶点法线[J]. 电脑知识与技术， 2013（23）：5331-5333.

[5] 程磊，刘海艳. 一种三维实体模型表面法线计算方法研究[J]. 沈阳理工大学学报， 2009， 28（4）.

【通联编辑：唐一东】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。