《机场出租车司机决策模型研究》-经济学论文，经济论文-论文范文参考-科学狗论文网

标题

机场出租车司机决策模型研究

范文

刘兴王亮策陈艳萍

[摘?要]文章针对机场出租车司机的选择排队拉客还是空车返回城区的决策问题，首先分析影响出租车决策因素，选取了航班数、时间段等确定型因素、出租车分担率和延误率等不确定性因素，得到了各个影响因素之间的关联关系和乘客数量的变化规律;其次建立等待时间模型，对出租车司机的等待时间进行预测;最后建立选择决策模型，以司机不同决策的期望收益为决策依据，给出司机的选择策略。

[关键词]选择决策模型;期望收益;机场出租车司机

[DOI]10.13939/j.cnki.zgsc.2020.22.031

1?引言

大多数乘客下飞机后要去市区的目的地，出租车是主要的交通工具之一。[1]国内多数机场都是将送客与接客通道分开的。送客到机场的出租车司机会面临两个选择：一个是前往到达区排队等待载客返回市区;另一个是直接放空返回市区拉客。文章分析研究与出租车司机决策相关因素的影响机理，分析影响出租车决策因素，选取了航班数、时间段等确定性因素和出租车分担率和延误率等不确定性因素，综合考虑机场乘客数量的变化规律和出租车司机的收益，建立了出租车司机选择决策模型，并给出司机的选择策略。

2?问题描述

针对到达机场的出租车司机的决策，如果选择前往到达区排队等待载客返回市区，那么出租车必须到指定的“蓄车池”排队等候，依“先来后到”排队进场载客，等待时间长短取决于排队出租车和乘客的数量多少，需要付出一定的时间成本;如果选择直接放空返回市区拉客，出租车司机会付出空载费用和可能损失的潜在载客收益。

2.1?符号说明

3构建机场出租车司机选择决策模型

3.1?影响出租车司机决策因素的分析

在实际中，有许多影响司机决策的因素，本节将其分为确定因素与不确定因素，分别进行分析。选取的确定因素包括航班数量、时间段、蓄车池已有车辆数;选取的不确定因素包括出租车分担率。

3.1.1?航班数量和时间段

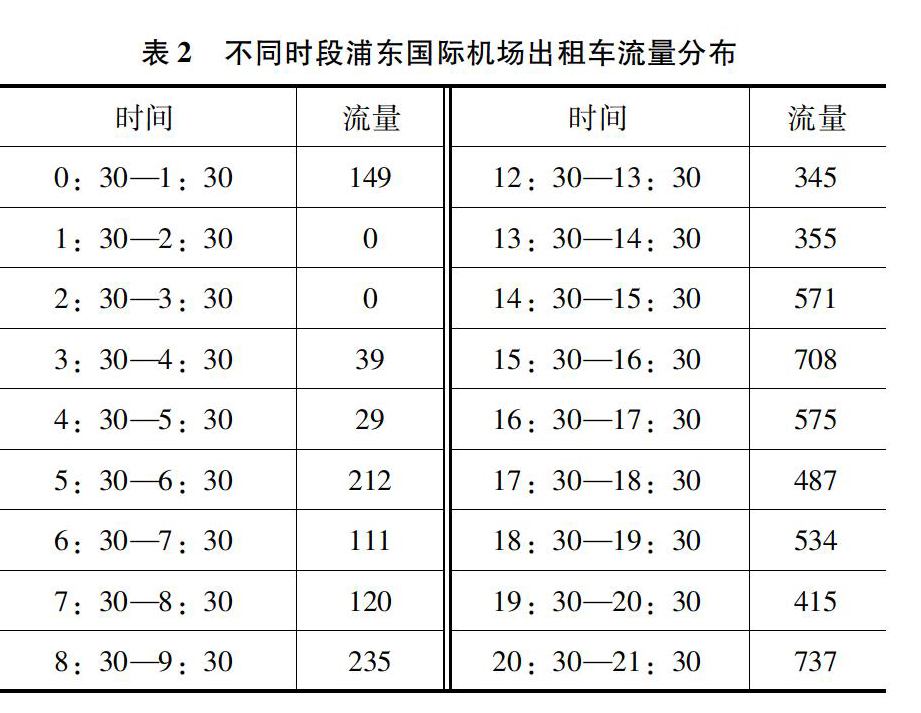
機场出租车需求量与航班高峰的高度吻合，即到港或起飞的飞机数量多，则机场出租车的需求量大。以浦东国际机场为例，表2表示各时段浦东国际机场的出租车流量分布。

从表2可以明显看到，出租车16：30—17：30与22：30—23：30两个时间段出现高峰，入港与起飞飞机架次的高峰出现在12：30—0：30、10：30—11：30、15：30—16：30、21：30—22：30，由于乘客下飞机之后需要办理一系列的手续，乘客离开机场的时间需要往后推迟1小时左右，因此，下飞机乘客对出租车的需求量具有一定的滞后性，这与出租车的需求高峰期16：30—17：30与22：30—23：30是吻合的，且在23：00之后，地铁和公交车等公共交通停运，造成出租车的分担率上升，因此出租车的需求量在22：30—23：30出现激增[1]。

将落地航班数量直接影响着下机乘客的多少，根据航班信息，出租车司机可以推测出即将下飞机的乘客数量，n为即将下飞机的乘客数量，ni为第i架次的航班的载客数量，下飞机乘客数量的函数表达如式（1）所示：

n=∑ni（1）

各个机场由于所处的地理位置以及机场附近的公共交通不同，出租车的分担率也不同，乘坐出租车人数与下机人数成正相关，因此，抵达机场的航班数量越多，司机决定等待载客的可能性越大。N表示选择乘坐出租车离开机场的乘客数量，α1为目标机场的出租车分担率，N与α1的函数关系如式（2）所示：

N=n×α1（2）

3.1.2?蓄车池已有车辆数

蓄车池已有车辆的数目与出租车司机的等待时长成正相关，在乘坐出租车乘客充足的情况下，出租车司机的等待时间主要为排在前方出租车的上客时间，T1表示蓄车池已有出租车的上客时间， m表示蓄车池已有出租车数量，v表示一辆出租车的上客时间，本节据此得到m与v的函数关系如式（3）所示[2]：

T1=m×n（3）

3.1.3?出租车分担率

不同机场所处的地理位置不同，导致机场不同交通工具的分担率也不同[4]，以浦东国际机场为例，虹桥机场距离市中心约55km，对于出租车的依赖性大于其他交通枢纽，因此，虹桥机场的出租车分担率高达36%;以双流国际机场为例，双流国际机场连通成都地铁十号线和高铁，可以在航站楼直接换乘地铁或者高铁，因此，双流国际机场的出租车分担率较虹桥机场偏低，为22%。

3.2?机场出租车司机等待时间预测模型

通过对航班数量和蓄车池已有车辆的分析，可以获得出租车司机等待载客的时间。Tw表示出租车司机等待载客的时间，指出租车司机加入排队队伍到搭载乘客离开的时间。T1表示在蓄车池已有出租车的上客时间;由于航班延误等事件，可能出现某个时段出租车上车口无乘客排队上车的状况，此时所有蓄车池的出租车都处于等待状态，因此，T2表示出租车上车口无乘客上车时所耽误的时间。本节据此获得出租车等待载客的时间T，如式（4）所示：

T=T1+T2（4）

其中T1受到蓄车池已有车辆数目的影响，m为蓄车池已有出租车数量，v为每辆车上客所需时间，因此：

T1=m×v（5）

v1为乘客进入“乘车区”乘坐出租车的速度，ΔN表示在T-Δt，T+Δt时间段内选择乘坐出租的乘客数，ΔN随着时间点T变化，与出租车的分担率α和航班数，因此：

v1=ΔN2Δt（6）

ΔN=fT，α（7）

根据假设一，“乘车区”总是有出租车等待乘客，因此乘客乘坐出租车离开“乘车区”的速度恒定不变，为v2。v3为“上车点”排队队伍人数的增长速度，N1为“上车点”排队队伍人数，则：

v3=fT，α2Δt-v2（8）

N1=∫T0fT，α2Δt-v2dt（9）

当“上车点”排队队伍人数N1=0时，造成无人上出租车的情况，此时蓄车池所有出租车司机都处于等待状态，T2表示出租车上车口无乘客上车时所耽误的时间，如式（10）所示：

T2=f2N1=0（10）

综上所述，得到等待时间模型，如式（11）所示：

T=T1+T2T1=m×vT2=f2∫T0ft，α2Δt-v2dt=0（11）

3.3?机场出租车司机选择决策模型

从出租车司机的视角出发，司机会对比等待载客与返回市区拉客的期望收益，其会选择期望收益大的方案，因此，本节尝试比较等待乘客于返回市区拉客两种情景下的期望收益，并以此为依据，建立选择决策模型，并给出司机的选择策略。

3.3.1?确定等待载客的收益期望值

I1为出租车等待载客回市区的收入，D为出租车等待载客回市区的路程长度，结合出租车打表计价规则，得到I1与D的函数关系，如式（12）所示：

I1=f3D（12）

Cj为出租车等待载客回市区的路程成本，包括邮费等成本，Cj与D成正相关，得到Cj与D的函数关系，如式（13）所示：

Cj=f4D（13）

Ct与租车司机等待载客的时间T成正相关，q为出租车司机在市区拉客单位时间的平均收益，描述時间成本Ct与等待载客时间T之间的关系，如式（14）所示：

Ct=T×q（14）

综合以上分析，可以得到等待载客的期望收益E1，如式（15）所示：

E1=I1-Cj-CtI1=f3DCj=f4DCt=m×v+f4∫T0ft2Δt-v2dt=0×q（15）

3.3.2?确定返回市区拉客的收益期望值

由于出租车空车返回市区，因此需要承担空车返回市区的路程成本，载客返回市区的路程成本与空车返回市区的路程成本相同，由于空车返回市区，没有收入，因此返回市区拉客的期望收益值E2为负值，如式（16）所示：

E2=-Cj（16）

3.3.3?建立选择决策模型

出租车司机会比较等待载客与空车返回的期望收益，选取期望收益大的选择，决策模型如式（17）所示：

A=0E1E2（17）

当E1E2时，等待载客收益大于返回市区拉客收益，此时A取值为1，表示出租车司机选择等待载客。

综合式（14）（15）（16）（17），汇总得到选择决策模型，如式（18）所示：

A=0I1CtI1=f3DCt=m×v+∫∫T0ft2Δt-v2dt<0dt×q（18）

4?结论

本模型主要用于机场出租车司机根据各因素决策是否留在机场等待载客，以及帮助机场设计上车点以提高运输效率。类似的问题还有很多，文章为解决大部分运输点的设置，以及交通枢纽处的包括出租车、滴滴等司机的决策问题提供了思路。

参考文献：

[1]谢东昊.“互联网+”背景下传统出租车行业的困境及出路探析[J].中国市场，2016（41）：145-147.

[2]颜超.?上海市枢纽机场陆侧公共交通管理研究[D].上海：华东师范大学，2015.

[3]倪志伟.?基于排队论的订单处理系统建模与仿真[D].北京：北京交通大学，2009.

[4]?滴滴出行，第一财经商业数据中心，无界智库.知道—中国智能出行 2015 大数据报告[J].中国广播，2016（3）：95.

[基金项目]2020年四川师范大学大学生创新创业训练计划项目（项目编号：S202010636253）。

[作者简介]刘兴（1999—），男，汉族，四川成都人，研究方向：优化调度等。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。