《挑战性问题的设计探讨》-理学论文，中学数理化论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

挑战性问题的设计探讨

范文

王佳炜

[摘要]合理的学习内容是有效学习得以展开的前提条件.佐藤学先生曾说：“学习内容应该是高水准的，具有‘挑战性的学习任务.”教师应设计有深度、能探究的学习问题，让学生不断探索，从而促进学生有效学习.

[关键词]挑战性问题;设计;探讨

[中图分类号]? ? G633.6? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2021）05-0001-03

一、背景介绍

日本著名教育家佐藤学先生倡导在学校构建“学习共同体”.所谓“学习共同体”，是指学习者在教师、家长、辅导者等助学者的帮助下，通过彼此之间的沟通、深入的交流和学习资源的共享，形成相互作用、相互影响、共同完成学习任务，最后达到成员全面成长的学习团体.

受佐藤学先生的影响，笔者所在学校开展“微共体”协同学习教改实验八年有余，相关项目获全国课改项目“优秀创新奖”，课题获省教育科学研究优秀成果一等奖.“微共体”的核心内涵是学习共同体理論，倡导协同学习.而协同学习是符合学科本质的学习，是以倾听、对话为基础的学习，是富有“挑战性”的学习，是最高层次的学习.

二、问题提出

合理的学习内容是有效学习得以展开的前提条件，那么在协同学习模式下，教师应当如何设计教学内容呢？教师只有设计有深度、能探究的学习问题，才能让学生不断探索，促进学生有效学习.如果课程内容难度太低，就无法引发学生更深层次的思考，学生便不能从深度思考中获益，学习的动机亦会降低.

下面，笔者结合曾执教的一节复习课《觅圆》（圆的基本性质复习）中的一些教学片段谈谈如何设计挑战性问题.

三、课堂简录

本节课为中考第一轮复习中《圆的基本性质》专题复习，侧重于根据圆的概念构造辅助圆以及垂径定理、圆心（周）角定理的应用.由于是中考复习，必然涉及三角形、四边形等几何综合知识，因此综合运用是本节课的难点.

在简单回顾圆的概念和相关性质后，笔者借助例题“如图1，在△ABC中，[AB=AC]，以AC为边在△ABC外作等边三角形ACD，连接BD，则∠CBD=? ? ? ? ? ? ?.”引导学生发现并了解“共顶点三等线”的结构，根据“圆的半径处处相等”构造辅助圆，实现圆心角向圆周角的转化.之后，笔者便设置了挑战性问题.

挑战性问题：在四边形ABCD中，AB∥CD，[AC=BC=DC=4]，[BD=6]，求AD的长.（要求：①独立思考5分钟;②组内互学，观点分享;③组间分享，观点碰撞.）

教学片段：

学生独立思考后“微共体”内互学，随后在倾听的基础上，组间分享、补充、提升、完善.整个过程，笔者退在一边，把课堂完全交给学生.

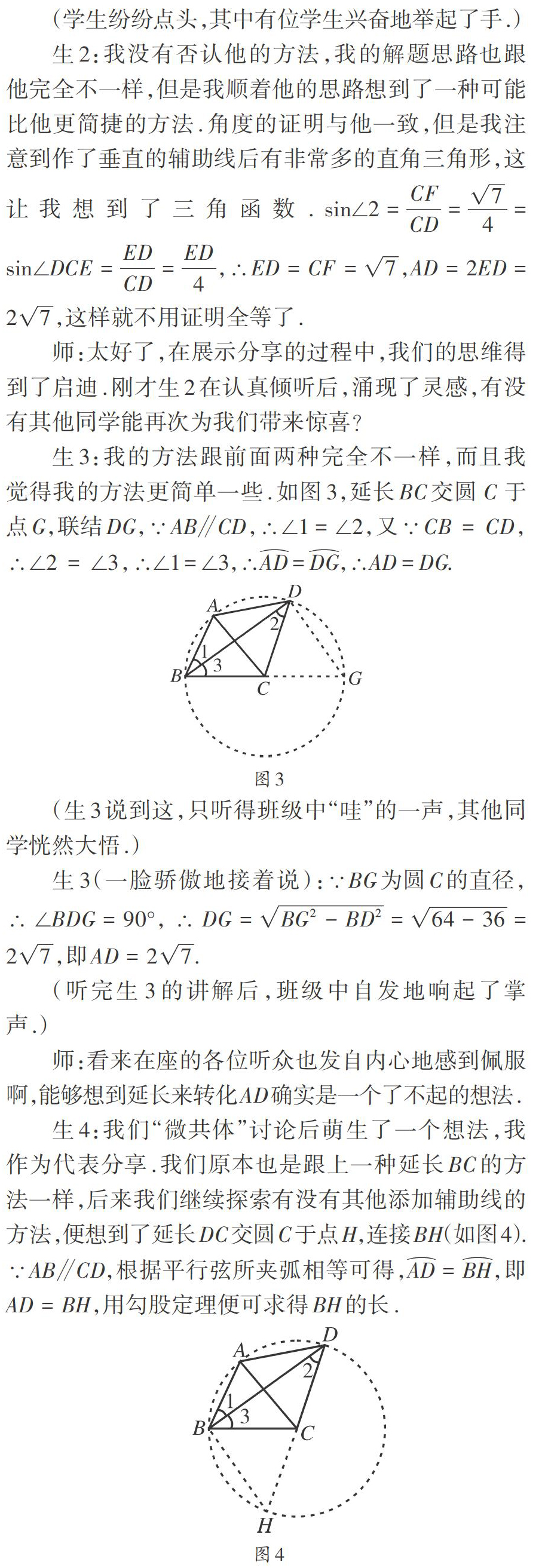
（听完生3的讲解后，班级中自发地响起了掌声.）

师：看来在座的各位听众也发自内心地感到佩服啊，能够想到延长来转化AD确实是一个了不起的想法.

生4：我们“微共体”讨论后萌生了一个想法，我作为代表分享.我们原本也是跟上一种延长BC的方法一样，后来我们继续探索有没有其他添加辅助线的方法，便想到了延长DC交圆C于点H，连接BH（如图4）.∵AB∥CD，根据平行弦所夹弧相等可得，[AD=BH]，即[AD=BH]，用勾股定理便可求得BH的长.

（生4短短的几句话却将问题解释得如此通透，实属不易，在座的各位学生自是掌声不断.）

四、挑战性问题设计分析

这道看似简洁的问题实则下足了功夫，并且进行了充分的预设.本问题所给条件及图形与例题较为类似，均根据“共顶点三等线”构造辅助圆，从而求得弦长，这在一定程度上给予了学生动手探索的知识与勇气.解题过程中，方法多样且综合性强.如利用垂径定理、借助圆周角定理证明全等完成线段转化，或是巧妙利用三角函数计算线段长，或是利用同弧所对的圆周角相等顺利转化线段，利用勾股定理求解，更有甚者充分利用平行，根据平行弦所夹弧相等转化线段.这些方法几乎涵盖了圆中所有的方法，在学生思考、尝试、分享的过程中收到了很好的复习效果.

若关注解法之间的联系，它们具有互相启迪的作用.如生2提出的三角函数法，是建立在生1所提出的推导方法之上，受其启发，萌生了较为简捷的三角函数法.而生3、生4所添加的辅助线——延长半径也有相似之处.这种类比，无论在组内交流，还是组间分享，都预留了充分的思维启迪空间，进一步促进学生思维的发散.

同时，作为一节中考一轮复习课，兼顾了全等三角形、三角函数、勾股定理、平行的性质等知识的运用，对于学生的综合解题能力也是较好的提升.作为挑战性问题，它具有一定难度，需要借助“微共体”协作分享，完善解题方法.

五、对挑战性问题设计的思考

挑战性问题是课堂教学的主线，是学生学习的疑点，是知识的连接点，是数学思想的聚焦点，也是教师钻研教材的着力点.

1.超前性与当前性相结合.学生是数学课堂教学中的主体，在“微共体”协作学习中更是如此，学生必须从内心深处对这种学习活动具有较强的自主性.传统观念认为，数学问题的设计要由易到难，即为学生铺石搭阶，让其拾级而上，达到知识的制高点.这种方法当然能够达到掌握知识的目的.但从素质教育的观点来看，“问题解决”教学模式中的问题设计也可以适当地反其道而行，即由难到易.

具体来说，首先给学生探索的问题不妨宏观一些，是一个综合性的超前问题，让学生感受到开展“微共体”协同学习的必要性.在学生遇到困难时，引导其步步分解为当前可以解决的问题，这就要求教师在设计问题时，必须遵循超前性与当前性相结合的原则，挑战的难度一旦超出学习者的认知范围，学习任务则无法引发深度的学习，过于简单的学习任务亦然.

2.生活性与抽象性相结合.生活即教育，数学来源于生活.无论是教学内容还是教学环节，都应该把学生的生活作为学习的出发点，这有助于激发学生的学习热情，促进学生有效理解数学问题，提升学生解决问题能力和实践创新能力的发展.因此，挑战性问题应当是现实的、有意义的，相关内容要有利于学生开展观察、实验、猜测、验证、推理、协作与分享等数学活动.

当然，数学课堂教学过程是从学生的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程.因此，挑战性问题也应当具备一定的可概括性，能够引导学生概括成已学习或是即将学习的数学知识或模型.学生经历回忆、联想、探究、协作、建模等过程，其实是不断接近数学问题的本质，与课标强调的“要让学生经历数学知识的形成和应用过程”相契合.

3.多样性与开放性相结合.学生存在好奇心理，为了激发学生的“微共体”协作学习热情，笔者常常适当增加挑战性问题的多样性.这里所说的“多样性”，既可以指问题提出形式的多样、问题内容本身的多样，抑或是解决问题的方法多样，无论选择何种途径，只要切合合作学习，都可以有效燃起学生的关注热情.

但是，不能一味地追求多样而忽略了问题的开放性.这里的“开放性”指的是“为了实现有深度的‘微共体协作学习，将课堂挑战性问题设计成具有探索性的内容”.在这样的问题思路引导下，学生的数学思维得以在“微共体”学习过程中灵动起来，使数学学习效果得到提升.在协作学习的氛围下，学生对于开放性问题的思路可能也多起来.

[? ?参? ?考? ?文? ?献? ?]

佐藤学.学校的挑战：创建学习共同体[M].钟启泉，译.上海：华东师范大学出版社，2010.

（责任编辑黄桂坚）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。