《基于改进QPSO的单任务Agent联盟生成》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于改进QPSO的单任务Agent联盟生成

范文

徐桓+孙瑜

摘要：针对群智能算法求解Agent联盟生成问题过程中易出现粒子过分聚集，导致多样性降低，甚至陷入局部最优现象提出一种基于改进量子粒子群的求解策略，在粒子过分聚集时借鉴实数编码遗传算法中的柯西变异使粒子聚集程度降低，进而维持了粒子的多样性。并采用多种群并行和最优粒子移民策略加快算法收敛。实验表明，该策略可以快速高效的求解Agent联盟，在运行效率上优于同类方法。

关键词：Agent联盟；量子粒子群；多Agent系统；柯西变异

中图分类号：TP18 文献标识码：A DOI：10.3969/j.issn.1003 6970.2015.02.001

1 概述

Agent联盟是求解单一Agent难以完成任务的一种有效方法。Agent联盟通过共享资源，共同构造求解方案等方法使整个系统能以最优或接近最优的配置和效率求解任务，获得最大利益。作为多Agent系统的关键问题之一，Agent联盟生成主要研究如何动态的生成一个最有联盟，使既定任务获得最优或较优值。自1993年提出联盟方法之后国内外学者做了大量研究，提出了多种算法。文献[3]提出了用粒子群优化算法（PSO）求解Agent联盟。文献[4]提出用量子粒子群算法（QPSO）求解Agent联盟。目前的算法往往得到一个与最优值相距一定限度内的次优解，存在联盟稳定性较差、收敛速度慢，全局寻优能力不强等问题。量子粒子群优化算法相对于PSO算法具有进化方程简单、需调节的参数少、收敛速度快等特点。在很多实际问题中都得到了优于PSO算法的结果。可以看出QPSO算法具有良好的稳定性和收敛性，通过设计相应的适应值函数可以很好的用于各种组合优化问题。不过，量子粒子群算法和粒子群算法一样同样存在陷入局部最优的情况。研究后发现上述情况主要是因为随着迭代次数的增加，粒子出现过分的聚集情况，导致多样性减少，进而陷入局部最优。本文通过引入一种对粒子过分聚集时的处理机制来维持粒子的多样性。实验表明该算法适用于求解Agent联盟问题，获得了很好的效果。

2 Agent联盟问题及量子行为粒子群算法相关概念

2.1 Agent联盟问题概念

3 基于改进的QPSO的单任务Agent联盟算法

相对于PSO算法，QPSO算法取消了速度变量，因此也不存在因速度受限而导致粒子搜索空间逐渐减小的缺点。但是在算法收敛的情况下，粒子都向现在的最优解方向飞去，损失了粒子的多样性，导致算法后期的收敛速度变慢，甚至到一定程度后无法继续收敛，陷入局部最优。因此，为了使得QPSO算法获得更好的解决Agent联盟问题的性能，本文做了如下改进：

3.1 多种群并行处理

QPSO比PSO有明显优势，但也存在陷入局部最优的情况。当某一粒子发现并向一个局部最优值接近时，其他粒子会向其靠拢，若在靠拢过程中没发现更好的位置，整个粒子群也会陷入局部最优。虽然陷入局部最优是群智能算法固有的特点，但也应该尽量避免。根据相关研究发现多种群并行搜索是解决陷入局部最优问题的有效解决方法。只要n个子种群没有任何2个陷入同一局部最优位置，整个粒子群陷入局部最优的概率会小于单一种群的1/n2。在多种群进化过程中，每N迭代便通过移民策略交换个子群中的最优粒子，即把全种群中最优粒子移民到其他子群中，同时保留各子群最优粒子。其中N的取值不宜太小，因为过于频繁的移民会导致粒子多样性减少，可能出现局部最优情况发生。

3.2 针对寻优过程中粒子过分聚集的处理

算法在迭代过程中，会因迭代次数的增加而使种群的多样性会逐渐降低，可能导致无法搜索到全局最优或经过很多次迭代才跳出局部的情况发生。实验发现上述情况的发生多是因为粒子迭代过程中过分的聚集在一起导致陷入局部最优造成的，为解决此问题本文提出一种处理方法。方法如下：

在迭代过程中检查算法的当前最优值，若最优值连续N代没有变化，则计算粒子的聚集程度；聚集程度的判断方法是计算当前种群中粒子适应值函数的均方差，公式如下：

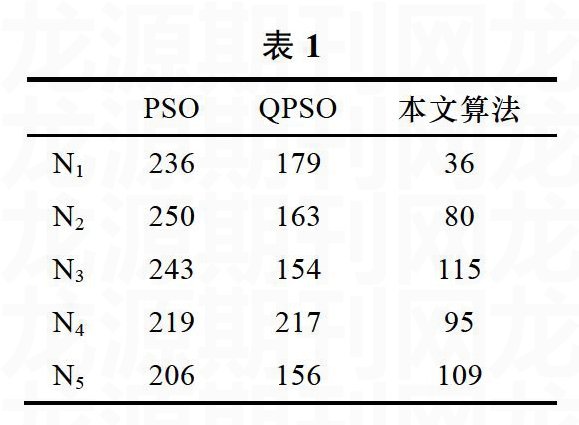
可以看出，即使任务需求向量，本文算法亦能在120代前收敛到最优解附近，节省了时间开销，且稳定性较强，计算的可实现性较好。综上所述，本文算法收敛速度更快，在解的质量上优于两种对比算法，且稳定性更高，不易陷入局部最优，能更有效的应对Agent联盟问题的求解。

5 结束语

本文通过对粒子过分聚集时的处理提高了量子粒子群算法的收敛速度，提高了算法效率，有利于快速求解单任务Agent联盟生成问题。下一步将研究多任务并行Agent联盟生成问题的量子粒子群算法及相应Agent对应策略。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。