《伪随机跳频序列特性及其在FH-CDMA系统中的应用》-工学论文，通信论文-论文范文参考-科学狗论文网

标题

伪随机跳频序列特性及其在FH-CDMA系统中的应用

范文

董桢

【摘要】跳频通信技术具有保密性高，抗干扰能力强，多址接入能力好等优势，在军事通信中已经广泛应用。跳频序列是保证跳频系统具有上述优势的关键。本文从跳频系统的需求出发，讨论伪随机跳频序列的性能指标及其数学关系，研究几类常见的伪随机序列（素数跳频序列，多项式跳频序列等）在跳频多址接入（FH-CDMA）系统中的应用。通过理论与仿真分析相结合，给出不同伪随机跳频序列的汉明相关特性对系统误码率性能的影响。

【关键词】跳频系统跳频序列汉明相关性误码率

一、概述

跳频（Frequency-hopping）通信是一种扩频通信技术（Spread-spectrum），系统的工作频点随着跳频序列在较宽的频带内随机跳变，敌方由于无法准确地估计和快速跟踪跳频系统的工作频点，从而实现了跳频通信的安全性和抗干扰能力。同时，跳频通信系统中每个跳频电台都预先分配了唯一条跳频序列，从而实现跳频系统的多址接入能力，跳频序列即是跳频用户的地址码[1]。众所周知，在码分多址系统（CDMA）中（包括直扩系统DS-SS和跳频系统），多用户干扰（MAI）是影响其性能的关键[2]。在跳频多址接入系统中，多用户干扰是由跳频频点的碰撞会带来的。因此在跳频通信实现中，为了实现跳频通信的优势，我们希望跳频频点随机性越强越好，跳频序列条数越多越好，跳频序列间频点的碰撞越少越好。

跳频序列性能的好环对跳频系统具有举足轻重的作用。虽然完全随机的跳频序列具有良好的统计特性，但是在现实中无法实现（收发端无法实现跳频图案同步），因此，实际系统中一般需要采用多种数学变化和数学技巧（移位变换[3]，有限域变换[4]等）来得到跳频序列，这类跳频序列可以用具体的数学算法描述，因此，我们称之为“伪随机跳频序列”。目前，关于跳频序列的设计与分析是学术界的研究热点，提出了多种具有良好特性的伪随机跳频序列的构造算法，如多项式跳频序列[5]，无碰撞区跳频序列[3]等。多条伪随机跳频序列构成“跳频序列集”。

本文结合跳频多址通信系统的需求，介绍了伪跳频序列特性与系统性能之间的关系。为了使得FH-CDMA系统满足保密性和多址能力要求，构造出伪随机跳频序列的各个参数需要满足一定的数值关系（理论下界）。分析了几类典型伪随机跳频序列（素数跳频序列，多项式序列等）的汉明相关特性，并将其应用与跳频多址接入系统中，通过仿真给出了基于上述几类伪跳频序列的异步2FSK-FH-CDMA系统的误码率性能。通过分析看出，满足跳频序列理论下界的伪随机跳频序列具有良好的误码率性能。

二、伪随机跳频序列参数的要求及其理论下界

在多个用户的跳频网络中，跳频集中的每条跳频序列分配给唯一用户使用。假设这样的跳频序列集S具有K条跳频序列，每条序列C（k）长度为L，则S可以表示为：

为了实现FH-CDMA系统具有良好的性能指标，跳频序列集的参数（序列个数K，序列长度L，频点个数q，最大汉明相关值H（ X ）和H（ X， Y ））需满足下述几个要求：

跳频序列集中的任意两个跳频序列X和Y，其汉明互相关值H（ X， Y ）尽可能小，即发生频率碰撞的次数少。

跳频序列集中任意跳频序列X，其汉明自相关旁瓣值H（ X ）尽可能小，即使得跳频序列准确同步。

跳频序列集中的序列数K尽可能多，即跳频系统能容纳更多的跳频用户。

频点集合F中的频点个数尽可能小，且每个频率出现次数，出现位置是均匀的，即实现跳频的随机性。

上述条件的最优值不可能同时满足，他们是相互制约的。通过严谨的数学分析发现，上述参数满足一定的数学关系，即满足Peng-Fan 理论下界。

定理1（Peng-Fan 界）[6]：令S是一个在大小为q的频点集F上的跳频序列集，其序列数目为K，序列长度为L，令I =「 LK/q」，则有

三、典型的伪随机跳频序列特性及其系统性能分析

本节首先给出几类典型的伪随机跳频序列的汉明相关特性，然后，通过仿真给出基于这几类跳频序列的BFSK-FHCDMA系统的误码率性能。

FH-CDMA系统收发端一般模型如图1所示。本文考虑FH-CDMA系统有K个跳频用户，发送端调制方式采用BFSK调制方式，一跳脉冲周期发送发送一个调制符号；解跳端采用非相干解调，信道考虑高斯加性白噪声（AWGN）。系统使用的伪随机跳频序列集表示为S={C（k）}k=M=S（q， M， L， Hm），其中q为跳频频隙集大小，K表示跳频序列个数，L表示跳频序列周期，Hm表示汉明自相关旁瓣/互相关最大值。

3.1伪随机跳频序列集

1）素数跳频序列

经典素数跳频序列集构造算法详见[1]，该序列集表示为

S1={{0，1，3，2，4}； {0，2，1，4，3}； {0，3，4，1，2}； {0，4，2，3，1}}

通过计算可得各个参数表示为：S1=S（q， K， L， Hm）=S（5，4，5，1）。该跳频序列在一个跳频周期内的平均碰撞概率为Hm/L=1/5。各参数代入（4）式可知，该伪随机跳频序列集满足Peng-Fan界，是汉明最优的跳频序列集。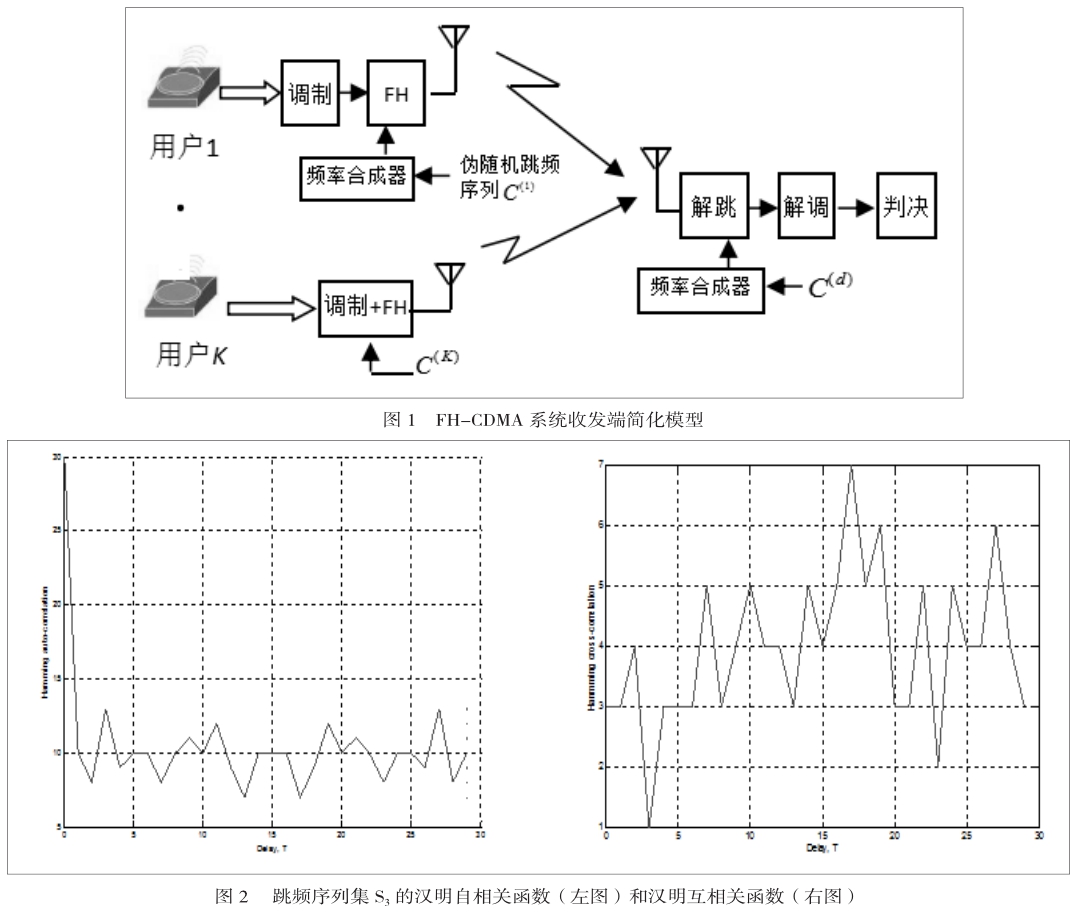

2）多项式跳频序列

文献[5]提出的一类三次多项式跳频序列集S2，如下所示：

S2={{2，3，3，0，1，3，1，4，4，0，3，4，3，2，2，0，4，2，4，1，1，0，2，1}， {4，0，0，2，3，0，3，1，1，2，0，1，0，4，4，2，1，4，1，3，3，2，4，3}，{1，2，2，4，0，2，0，3，3，4，2，3，2，1，1，4，3，1，3，0，0，4，1，0}， {3，4，4，1，2，4，2，0，0，1，4，0，4，3，3，1，0，3，0，2，2，1，3，2}， {0，1，1，3，4，1， 4，2，2，3，1，2，1，0，0，3，2，0，2，4，4，3，0，4}}；

通过计算该跳频序列各参数表示为：S=S（q， K， L， Hm）=S（5，5，24，5）。该跳频序列在一个跳频周期L内的平均碰撞概率为5/24，与素数跳频序列基本相同。该跳频序列集亦满足Peng-Fan界，是汉明最优的跳频序列集。

3）二进制序列映射成跳频序列

这类伪随机跳频序列是通过已有的二进制序列（如m序列，Gold码等）[1]，M个二进制数映射为一个2M多进制数，以此方法形成跳频序列集S3。这种跳频序列的构造算法比较简单，其最大的优势是跳频序列的长度L可以任意扩展，工程实现上应用该类跳频序列较多。但是这类跳频序列无法保证频点碰撞较低，也就是说，这类跳频序列在某些时刻下，会出现较大的频点碰撞；另外，该类跳频序列的频点随机性较差，易受到敌对干扰。一般情况下，该类伪随机跳频序列不满足Peng-Fan理论界。下面给出了一个二进制序列构造跳频序列的例子。构造出的 S3的序列个数K=5，序列长度L=30；频点个数q=5。该类跳频序列集中序列的汉明互/自相关函数曲线如图2所示。

从仿真图可以看出，最大汉明互相关值H（ X，Y ）=7，最大汉明自相关旁瓣值H（ X）=13，该跳频序列集S3不满足Peng-Fan理论界。与伪随机序列S2相比，该类跳频序列在某些时延下的汉明互/自相关值较大。

3.2基于伪随机跳频序列的FH-CDMA系统误码率分析

本小节考虑的BFSK-FH-CDM系统如图1所示。跳频系统中用户个数为K，且跳频多用户是异步接入系统。另外，假设接收端的参考用户为用户d=1。采用Matlab仿真分析方法，分别对采用上述三种伪随机跳频序列（S1，S2和S3）的误码率进行分析。为了合理比较，三种伪随机跳频序列的频点个数q，用户个数K基本一致。

从仿真图可以看出，采用跳频序列集S3的FH-CDMA系统误码率较高，这是因为在某些时延下，该跳频序列的汉明相关值较大，从图3也可得到这样的结论。采用跳频序列集S1和S2的FH-CDMA系统误码率基本相同，这是因为，这两个跳频序列集均满足Peng-Fan理论界，其频点的平均碰撞概率基本相同均等于1/5。实线曲线为没有频点碰撞时，FH-CDMA系统的误码率性能。采用特定的（准）正交跳频序列（如无碰撞区跳频序列），多用户FH-CDMA系统误码率可以逼近该性能下界。

四、结论

本文从跳频多址接入系统的性能需求出发，讨论了伪随机跳频序列性能对跳频系统的影响，介绍了伪随机跳频序列参数之间的制约关系。分析了几类典型跳频序列集的汉明相关特性。最后，将这几类跳频序列集应用与异步BFSKFH-CDMA系统，通过仿真分析，比较基于不同跳频序列的FHMA系统误码率性能。从分析可以看出，满足Peng-Fan理论界的伪随机跳频序列具有较低的频点碰撞概率，因此误码率性能较好。一般情况下，伪随机跳频序列构造都以满足理论界为设计指标。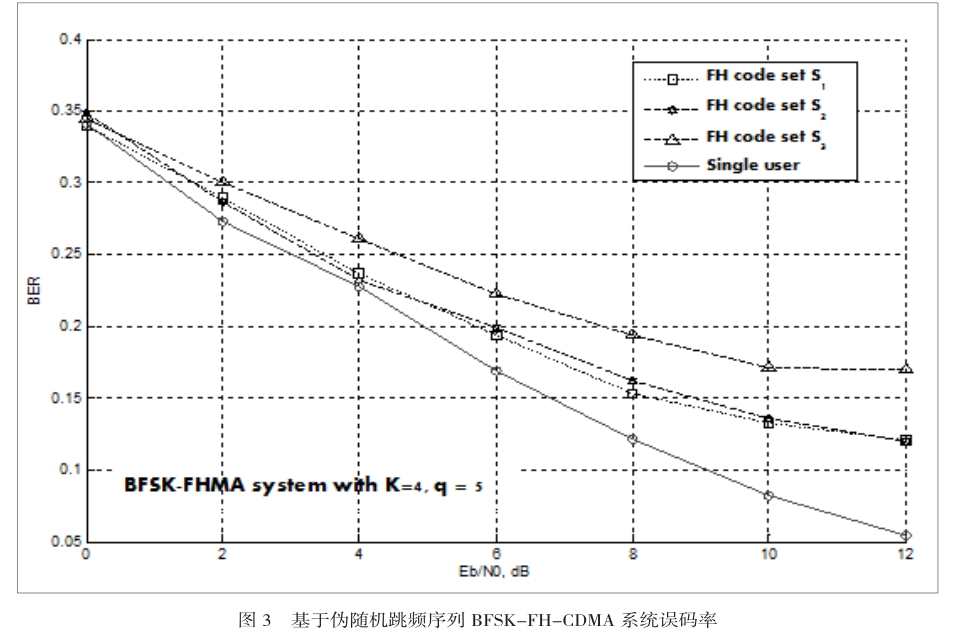

参考文献

[1] 梅文华，王淑波，邱永红等. 跳频通信[M]. 北京：国防工业出版社，2005.

[2] Choi K， Cheun K. Performance of asynchronous slow frequency-hop multiple-access networks with MFSK modulation[J]. IEEE Trans. Commun.， 2000， 48（2）： 298-307.

[3] Ye W X， Fan P Z， and Gabidulin E M. Construction of non-repeating frequency-hopping sequences with no-hit zone[J]. Electronics letters， 2006， 42（12）： 681-682.

[4] 梅文华，杨义先，周炯磐. 跳频序列设计理论的研究进展. 通信学报. 2003，24（2）：92一101.

[5] PENG D Y， PENG T， FAN P Z. Generalised class of cubic frequency-hopping sequences with large family size[J]. IEE Proceedings - Communications， 2006， 152（6）： 897-902.

[6] 彭代渊，范平志，李门浩. 低碰撞区跳频序列集周期汉明相关函数的理论限[J]. 中国科学， 2006， 36（1）： 1-11.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。