《顺学而教，聚焦核心素养》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

顺学而教，聚焦核心素养

范文

魏星

【摘要】学生的学习应该是由内心生发、自然而然、水到渠成的.课堂中教师需顺应学生的语言，聚焦核心问题;顺应学生的作品，在比较与交流中明确优缺点;顺应学生的抽象水平，搭建“脚手架”;顺应学生的错误，突破认知难点.

【关键词】核心问题;顺应学生;核心素养

作为一名“新手”教师，笔者对课堂教学的疑思总是层出不穷，很多时候在听完一节课后，往往感觉这节课上得真好，可具体好在哪里说不出来.下面以苏教版三年级数学上册“两位数除以一位数（首位不能整除）”一课为例，谈谈笔者在听课后的思考及深度钻研教材后的心得.

一、顺应学生的语言，聚焦核心问题

【片段1】

（学生从现实情境中抽象出了除法算式52÷2，教师引导学生借助小棒探究算法）

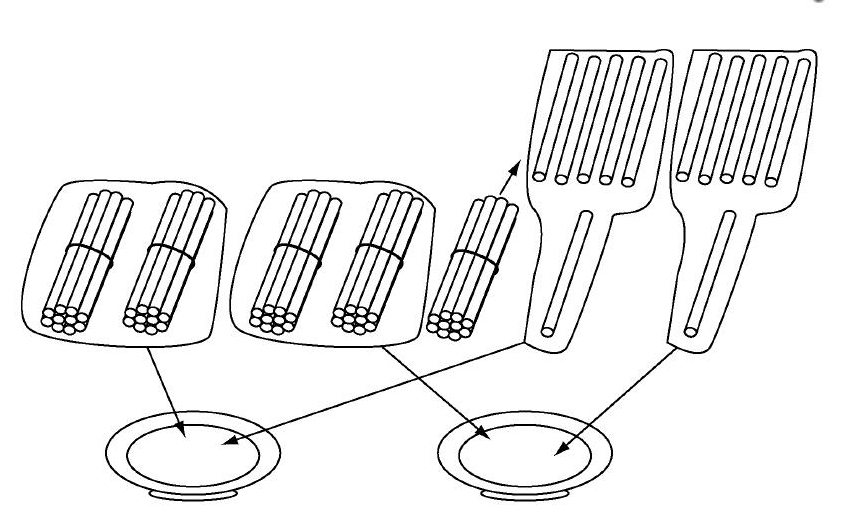
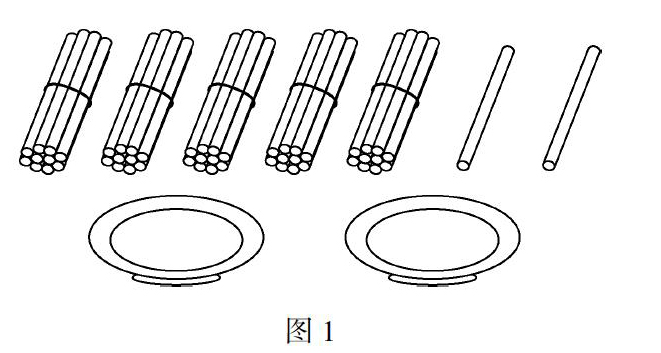
师：（出示小棒图，如图1）把小棒分放到两个盘中，你会分吗？

生：需要拆开分.

师：有没有必要全部拆开？

生：没必要，全部拆开太麻烦了，只拆一捆就行.

顺应学生的语言，程老师的问题：“有没有必要全部拆开？”就像文章开篇点题一般，学生自然在脑海自然想到要怎么拆，怎么拆是有必要的拆.

如何“拆”和“分”就是本课要解决的核心问题.学生此前已经学过“两位数除以一位数（首位可以整除）”，因此对除法竖式有知识基础.与之前的课相比，首位不能整除的问题的实质就在于首位有余数.余数可以继续除吗？怎么除？学生无法通过抽象的数字直接想到余数有什么意义，必须借助具体的实物学具小棒来理解.“首位不能整除”这句话用小棒“翻译”，就是有整捆的小棒多出来，没法继续均分.整捆的分不了，可以把这一捆拆为单根来均分.“分”的任务产生了“拆”的需要（见图2）.

一个“拆”字蕴含着“退一做十”的十进制思想，蕴含着计数单位的变化.它是知识的生發点，是突破算理的关键点，也是本节课需要探讨的核心问题.只有拆与分的过程清楚了，才能有后续的教学，才有竖式的抽象化表达.史宁中曾说：“运算律是算理，算理是运算本质，算理与运算等价.”由“拆”“分”而来的算理是本节课的思想基石，就如同一篇文章的线索贯穿文章.

二、顺应学生的作品，比较与交流中明晰

【片段2】

师：他们的分法（见图3，教师顺应学生的语言，将两种分法用小棒呈现在了黑板上）有什么相同点？有什么不同点？

生1：都先分了4捆.

生2：都要拆开一捆.

师：是的，都拆开了一捆（板书：拆），不同点呢？

生：一种只分了两次，一种需要分三次.

师：你们更喜欢哪一种方法？

生：我喜欢分两次的方法，更简单.

师：都同意？（生点头）那我们下面就重点研究分两次的过程怎么记录.（师将黑板上分三次的小棒图擦掉）

顺应学生在课堂上自然生成的作品，运用比较的方法让学生深入知识的本质.这里的问题指向明确：突出核心、优化算法.在遇到不同的算法时，让学生比较、交流相同与点不同点，一方面可以让学生再一次从头到尾经历算理形成的过程，另一方面可以在提取本质信息（即相同点）的同时，比较发现不同算法的优劣，自然而然地优化算法，非常巧妙地解决了除法为什么要从高位算起的问题.学生对核心问题“怎么拆、怎么分”的感受更立体、更深刻.

三、顺应学生的抽象水平，搭建脚手架

【片段3】

师：你能用算式来记录“分”的过程吗？

生：5÷2=2……1

师：这里的5是什么？5个1吗？

生：5是5捆小棒，也就是5个十，除以2表示把它们平均分成两份，每份是2捆，也就是2个十，剩下的一捆也就是1个十.

师：接下来怎么办？

生：把剩下的一捆拆开，变成10根，10+2=12，再把这12根平均分，12÷2=6，最后得20+6=26.（教师随着学生的话板书，见图4）

5个十÷2=2个十……1个十

1个十=10个110+2=12

12÷2=6

20+6=26

研究完拆分的方法后，顺着学生的话，教师用分步算式将分的过程记录下来，这是第一层次的抽象过程.对学生来说，直接将直观的小棒形象抽象为竖式是非常困难的.

以分步算式的形式连接直观的小棒和抽象的竖式，以此为“脚手架”，降低学生对每一步竖式计算的理解难度.学习是一个循序渐进的过程，学生的体验不是一蹴而就的，需要一层层铺染、加重，最终水到渠成.

四、顺应学生的错误，突破认知难点

【片段4】

师：和大家分享一下，你是怎么想的？

生1：我先用5÷2=2……1，再用2÷2=1，得数是21（见图5）.

师：谁来评价一下她的方法.

生2：应该还要用5-4=1，5捆分了4捆，还有1捆没有分呢.

师：结合小棒图找到了疑点，那应该怎么算呢？

生3：5个十减4个十等于1个十，也就是10个1，10再加2等于12，再用12除以2得6.（教师顺应学生的语言，结合小棒图，用红笔记录并纠正学生的作品，见图6）

5个十÷2=2个十……1个十

1个十=10个110+2=12

12÷2=6

20+6=26

课堂上，一名学生在计算时没有将十位的余数“1”落下来.这个错误出现的原因是该名学生对“1”无法再均分感到困惑，这是该名学生产生认知冲突的关键点.“1”明明分不下去了，可是当我们把它的计数单位进行转换，将“1个十”变成“10个一”，便可以进一步均分，也就是将“一捆”变成了“10根”.

在师生共同研究交流的过程中，学生最终明白了竖式计算每一步的含义，通过和小棒、分步算式的联系，真正建构起有关于两位数除以一位数（首位不能整除）的完整过程，理解了算理和计算方法.“数学里最高境界的横向关联结构化，就是数与形的关联结构化”，算理算法的研究虽是数的范畴，却离不开形的支撑.以生为本，顺应学生的错误，将它作为课堂宝贵的学习资源，学生自然能突破认知难点.

五、把握核心内容，提升学生的核心素养

从数的整体运算看，本节课的教学内容属于除法运算，涉及的数都属于自然数域.因为除数是一位数，所以这里把除法的意义理解为均分，学生用的直观模型是小棒.如果除数是小数、分数，那么要把除法的意义理解为包含除法，即每份数一定，求包含多少个这样的份数.

之前课时的学习中不涉及计数单位的转化.整十、整百数除以一位数，两位数除以一位数（首位可以整除）都是将同一数位上的数进行均分，因此学生较容易理解.首位不能整除的情况产生了转化计数单位的需要，因为首位的余数不能再以“十”的位值来进行均分，必须要将“1个十”转化为“10个一”.这一过程中，计数单位变了，数的大小不变，再和个位上的几个“一”合起来进行二次均分.

显然，后续两位数、三位数除以一位数，三位数除以两位数的计算中都涉及计数单位的转化，这是均分的必然结果.再往后，学习小数后，计数单位不仅要转化，还要进一步细化，基于生产、生活的精确化数据需要，数系的扩充势在必行，这就要求我们对整数除法中的余数进一步均分，将“1个一”转化为“10个0.1”，“1个0.1”转化为“10个0.01”等.

深入探究除法运算的本质，“均分”“计数单位”这些核心内容贯穿始终，教师在教学中要牢牢把握住学科本质，顺应学生的思维生长的规律，促进学生知识、方法、原理的自主迁移，发展学生的数学核心素养.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。