《初三数学中考专题复习课》-教育论文，科学教育论文-论文范文参考-科学狗论文网

标题

初三数学中考专题复习课

范文

黄国飞

摘要指导思想和理论依据：专题复习，是教师整合专题的主要知识点，引导学生内化专题的知识结构，以期达到对专题知识进行深化或是对专题知识进行迁移和创新。专题复习会引导学生追根溯源，感悟知识的联系，根据相同的知识点或运用相同的数学模型，对不同背景、不同层次问题的处理方法进行归纳，形成不同专题研究的内容数学思想或数学模型等形成解决策略的结构化，从而增强学生知识的迁移能力。

关键词数学中考《旋转相似》

中图分类号：G633.6文献标识码：A

《义务教育数学课程标准（2011年版）》（以下简称《标准》）中指出，在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。本节课拟以《旋转相似》为专题，引导学生合理构建数学模型，并能运用模型到具体题目中，同时学生的思维能力及解题能力有较大的发展。把握基本几何模型是落实“基本数学活动经验”的有效路径，是解决综合问题的有效策略。“旋转相似”既是相似图形的拓展，也是位似变换的特例。创造性的运用“旋转相似”模型对发展学生思维能力有着重要意义。中考专题复习过程中，“一个模型，多种题型”是学生解题重要的思维方式，因此此类专题复习课，对学生来说很有必要。

课程设计

教学目标：

（1）认识一类典型的图形——“旋转相似”模型及其基本结论。

（2）能在较复杂的图形背景下识别并抽离出该模型。

（3）掌握该模型的应用，会用该模型解决相关的一些几何问题。

教学重难点：

（1）在较复杂的图形背景下识别并抽离出该模型。

（2）会用该模型解决相关的一些几何问题。

教学过程：

1探究建模

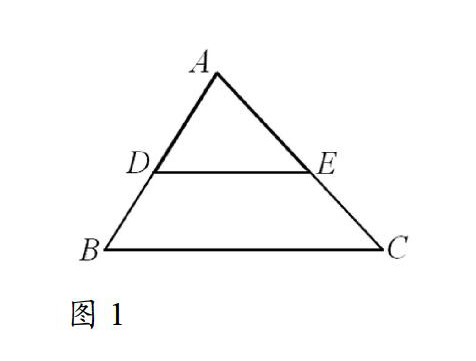
如图1，在△ABC中，DE//BC，请找出图中的相似三角形。

变式1 若将图1中△ADE绕点A旋转一定角度到如图2所示的位置（点D在△ABC的内部），连结BD，CE，图中还有哪些相似的三角形，请简要说明理由。

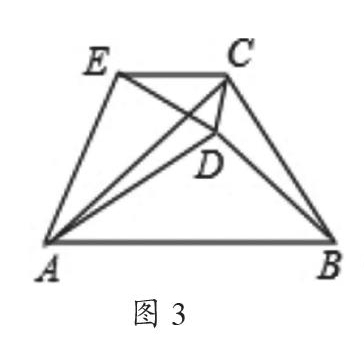
变式2若将图2中△ADE绕点A继续旋转到如图3所示的位置（点D在△ABC的外部，B，A，D不在同一条直线上），连结BD，CE，变式1中的结论还成立吗？

思考：在变式1、变式2中，由“旋转”得到的这对相似三角形有什么共同特征？

建模：（1）有公共顶点;（2）夹旋转角的两边对应成比例。

2模型识别

判断下列图形中有没有“旋转相似”模型？若有，请写出这两对相似三角形（可以添辅助线）。

（1）△ABC和△ADE都是等边三角形

（2）△ABC和△CDE都是等腰直角三角形

（3）△ABC和△ADE都是顶角为的等腰三角形

（4）正方形ABCD和等腰直角三角形△AEF

3模型應用

例题：

如图1，在Rt△ABC中，∠ACB=90埃珹C=BC，在斜边AB上取一点D，过点D作DE∥BC，交AC于点E。现将△ADE绕点A旋转一定角度到如图2所示的位置（点D在△ABC的内部），使得∠ABD+∠ACD=90啊？

（1）若CD=1，BD=，求AD的长;

（2）如图3，将原题中的条件“AC=BC”去掉，其它条件不变，设，若CD=1，BD=2，AD=3，求k的值;

（3）如图4，将原题中的条件“∠ACB=90啊比サ簦渌跫槐洌簦鐲D=m，BD=n，AD=p，试探究m，n，p三者之间满足的等量关系。（直接写出结果，不必写出解答过程）

小结。

变式1：如图1，正方形ABCD与正方形BEFG的边长分别为4和2，点E在BC边上，点G在AB边上，把图1中的正方形BEFG绕点B顺时针方向旋转角（0o< <60o），如图2，求AG：DF：CE的值。

变式2：若把变式1中正方形改为平行四边形ABCD和平行四边形GBEF，且AB：BC=GB：BE=m：n，∠ABC=∠GBE=60o（如图3），然后把平行四边形GBEF绕点B顺时针旋转（0o< <60o）（如图4）。求AG：DF：CE的值。

4课堂小结

（1）“旋转相似”模型的图形特征;（2）识别出“旋转相似”模型后，通常通过? ? ? ? ?（知识点）来解决问题。

运用建模的数学思想可以将复杂问题简单化，将未知转化为已知，它也能提高我们的数学应用能力和创新能力.我们在解题的过程中，要遵循我们的认知规律：一方面，我们要注意以解决问题为契机建构知识，并学会联系与联想;另一方面，我们应该掌握分析问题的途径，经历思考和选择的过程，从多种方法策略中寻找和筛选合适的解决方案，从而将问题逐步分解加以解决。

在《义务教育数学课程标准（2011年版）》中提出的10核心词中，几何直观和模型思想被作为要求提出，可见合理利用已有知识解决陌生问题也是中学生应具备的素养之一，怎样在教学过程中，让学生形成具有综合性阶段性和持久性等特征的数学学习能力与数学思想，应该成为教育工作者追求的目标.通过上述分析可以发现，在大多数情况下，还需要从基本模型人手，分析已知的模型与未知的问题之间的关联，借助熟悉且通用的方法获得实用的解决问题途径。综上所述，对中考数学题目的研析，让我们体会到基于数学核心素养之下的数学中考命题的新脉动，激发了教师对于数学核心素养的学科教学研究，以及学生数学核心素养提升的学习实践。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。