《一堂阅读材料课引发的二次思考》-教育论文，科学教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

一堂阅读材料课引发的二次思考

范文

张磊

摘要本文是一篇选自必修2第一章《空间几何体》中的阅读材料《祖暅原理与柱体、锥体、球体的体积》。它是在学生已经初步学习了柱体、锥体、球体的体积公式的基础之上对体积公式的由来做进一步探究，主要是引用祖暅原理推导出柱、锥、球体的体积公式。

关键词祖暅原理阅读材料课二次思考

中图分类号：G623.2文献标识码：A

1简述教学流程

引入：（1）请一位同学帮我洗一副扑克牌;（2）谁能帮助我求得这幅杂乱的扑克牌的体积？（学生很快回答：还原成整齐的长方体即可）;（3）由这一生活趣事引出祖暅原理。

介绍祖暅原理：用PPT展示祖暅原理的形成、祖暅原理的内容（通过形成经历来充实材料，让学生更了解祖暅原理，知晓祖暅原理中所蕴含的微积分思想，同时也增强了可观性和趣味性）

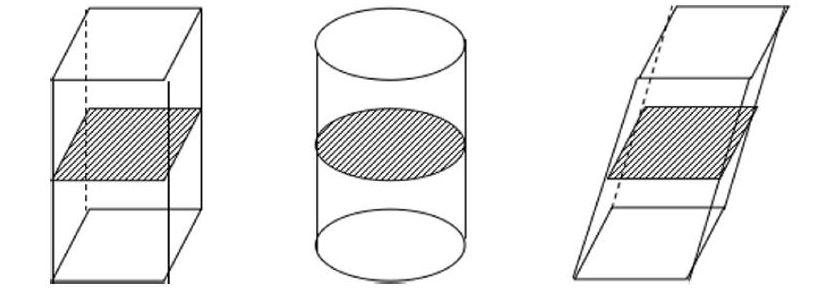
确认祖暅原理的条件：（1）归纳平面图形中夹在两平行线间的两个平面图形的面积相等的条件;（2）归纳空间图形中夹在两平行平面间的两个几何体体积相等的条件：

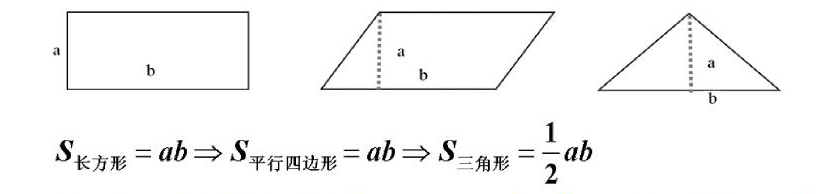
探究活动1：你是否能利用长方形的面积来探究平行四边形、三角形的面积呢？

（三角形的面积探究中运用了几何解题中的常用方法补形法。从简单的平面图形的面积下手，再过渡到空间几何体的体积，更容易让学生接受，并从中初步体会祖暅原理的应用）

探究活动2：通过平面与空间类比，再利用祖暅原理，尝试利用长方体的体积来探究柱体、锥体的体积？

（经探究1的铺垫，探究2进行很顺畅。尤其是锥体体积探讨，类比三角形面积求解时运用的补形法，学生很容易联想到可以将三棱锥补成柱体便可求解体积公式。）

探究活动3：能否再次利用祖暅原理来探究球体的体积呢？

（这一环节花了很长时间，尝试引导学生能否找到一个能够求体积的，使它和半球高度一样，并且用任何一个水平面去截它们是得到的截面面积都相等的几何体。几次引导几乎没什么进展。为帮助学生形成思路，借助几何画板的演示展示思路和求解过程）

总结延伸：（1）祖暅原理在解一类几何问题中的作用;（2）课后作业：结合球体体积的探讨过程尝试再次利用祖暅原理探究椭圆的体积公式。

（在求面积或体积的题目中，能恰当的引用祖暅原理可帮助我们将复杂的问题简单化）

2课后感受

这类的阅读材料教材中安排了不少。很多教师都认为它与高考没太大的关系，更何况现在教学任务重，上到这一块儿时要不就选择“避而不见”，要么就要求学生课下阅读。我认为别看它小、少，但作用不容忽视。高考对于数学文化并不是不考，只不过侧重于考查学生的数学思想和数学方法的迁移能力。而阅读材料中就蕴含着一些解题思想和方法，拿《祖暅原理》来说，它本身就是一个探究性的问题，内容的探究符合新课程的教学要求。通过教学，可以起到以下三方面的作用：（1）让学生了解了柱、锥、球体的体积公式的由来，强调了知识形成和获得的过程，使学生一贯的“数学就是死记公式—套用公式”思想转变为“数学可以是理解公式—活用公式”;（2）掌握求面积或体积一类问题的妙法，提高学生的类比、转化、整合能力，有助于解题思想的形成;（3）增加数学的趣味性，拓展学生的知识面，了解数学史激发学生爱国热情，并增强学习数学的信心。

教师在选择上这些阅读材料时应做好以下几个工作：

2.1课前认真备课

教材中安排的一些“阅读与探究”通过介绍一些历史人物、生活趣事在传达着某种数学问题，在研究这类问题的同时形成数学思想方法，并能用于解题。教师在备课时就要注意它安排的意图，尤其是与前后知识的关联。我们可以借助网络查询一些相关资料及背景来充实材料;还可以借助一些杂志来帮助我们进一步体会它的应用和迁移。只有我们充分备课，认真钻研，才能更好的发挥它的地位和作用，让学生学有所获。

2.2注重探究过程

大部分閱读材料都是探究型的，它内容新颖，学生首次接触，学生作为主体教师还是应该将探究过程交给学生，给予他们一定的空间来思考，尽量不要直接给出解题过程。探究的过程也是学生思维形成的过程。

总之，教材中的阅读材料是与教材相关的数学文化以及某些数学知识的延伸、拓展与应用，是教材知识结构的重要组成部分，与教材内容相互补充、融为一体。我们应当正确认识到阅读材料的地位与作用，认真研究它的内容，充分理解设计的指导思想和要求，重视阅读材料的教学，让它真正发挥其应有的教育功能和价值。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。