《古典概型教学方式研究》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

古典概型教学方式研究

范文

刘美玲

【摘要】本文探讨古典概型中概率如何求解的教学方式。针对排列组合数适用性难分辨、条件概率类型题目计算烦琐易出错的特点，举例说明不同类型题目如何正确使用法则。

【关键词】古典概型；排列组合数；条件概率

古典概型也叫传统概率或等可能概型，其定義是由法国数学家拉普拉斯（Laplace）提出的。内容简单，但数学题目千变万化，在多年的教学实践中发现，学生在古典概型的概率求解中依然存在很多问题。

一、古典概型定义

（1）试验的样本空间只包含有限个样本点；

（2）试验中每个基本事件发生的可能性相同。

具有以上两个特点的试验称为古典概型或等可能概型。

这里解释基本事件的发生概率相同，所以一个事件的概率值即是事件所含基本事件的个数除以基本事件总数。常见的古典概型有掷硬币试验、掷骰子试验、摸球试验等。具体的计算举例说明，以下两个例题分别取自参考教材[2][3]。

例1：设袋中有10只球，编号分别为1，2，…，10. 从中任取3只球，求：

（1）取出的球最大号码为5的概率；

（2）取出的球最小号码为5的概率；

（3）取出的球最大号码小于5的概率。

（3）由于取出的三只球中，最大号码小于5，C所包含基本事件的个数为，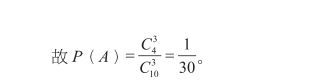

本题目中取球的方式是任意的，每个球被取到的概率都是一样的，所以是古典概型。另外，只要观察取出来的号码，没有顺序问题，所以用组合数计算。下面再看另一个例题：

例2：一个家庭中有两个小孩，已知其中一个是女孩，问另一个也是女孩的概率是多少？（假定生男生女是等可能的）

解法1：由题意知，样本空间为：

Ω={（男，男），（男，女），（女，男），（女，女）}

A表示事件“至少有一个是女孩”，B表示事件“两个都是女孩”，则有：

本题目解法1用古典概率公式计算，较为烦琐。实际上，这是典型的条件概率问题，用条件概率公式则可以简洁地计算出结果。条件概率在后续的学习中经常用到，例2是一个曾经在网络盛传过的小题目，这里经过条件概率的理论解释和计算，想必大家都能了解什么是条件概率了。条件概率的计算和应用是非常多的，全概率、贝叶斯以及随机变量的计算中都会用到，所以从这个例题引出其重要性和基础性，激发学生认真学习、理解透彻。

【参考文献】

[1]刘倩.由古典概型引入贝叶斯公式的一种教学设计[J].高师理科学刊，2016，36（6）：56-60.

[2]吴传生.经济数学（概率论与数理统计）（第三版）[M].北京：高等教育出版社，2016.

[3]朱泰英，周钢.概率论与数理统计[M].北京：中国铁道出版社，2015.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。