网站首页  词典首页

请输入您要查询的论文：

　

标题 台湾地区高考数学试题特色赏析
范文 台湾地区针对大学招生每年有两次大的考试.一是每年1、2月份的大学学科能力测试（简称“学测”），二是每年7月初的指定科目考试（简称“指考”）.“指考”数学考试分数学甲（理科程度）与数学乙（文科程度）.学生如果通过“学测”没能被理想的大学提前录取，他们还可参加“指考”，寻求第二次被理想大学录取的机会.
台湾地区学生在大型国际测试项目TIMSS和PISA中，一向成绩名列前茅.这说明台湾的数学教育质量非同一般.本文以台湾近五年高考数学试题为分析文本，来探究、赏析岛内高考数学试题的特色.
特色1单选题与多选题并存
“学测”数学试卷由单选题、多选题、选填题三类题型构成，用时100分钟，总分100分；“指考”试卷也包括了这三类题型，且多了两个解答题，用时80分钟，总分100分.
单选题与多选题都有5个选择支.多选题在大陆高考试题中很少出现.以2016年而言，“学测”试题中多选题7个，占分35分；“指考”数学甲试题中多选题3个，占分24分；数学乙试题中多选题5个，占分40分.可见多选题占分不少.
例1（2016年“学测”单选题第6题）设{an}为一等比数列.已知前10项的和为∑10k=1ak=80，且a1+a3+a5+a7+a9=120，请选出首项a1的正确范围：
分析a2+a4+a6+a8+a10=q（a1+a3+a5+a7+a9），则（1+q）（a1+a3+a5+a7+a9）=801+q=23q=-13，由a1+a3+a5+a7+a9=120a11-（q2）51-q2=120，有
a1=1201-191-195=120×89-194>120×89>100，

排除（1）、（2）、（3）.
又9-194>8a1=1201-191-195=120×89-194
<110，排除（5）.
正确答案是（4）.

例2（2016年“学测”多选题第7题）下列各方程式中，请选出有实数解的选项：
分析这个题如果分类讨论去绝对值符号，就比较麻烦.考虑到|x|、|x-5|的几何意义：分别表示点x到点0、5的距离.这样（1）、（4）是不可能的，有实数解应选（2）、（3）、（5）.

台湾选择题突出核心数学概念，强化基础知识与基本技能的考查；有些问题依托数学模型，注重数学思想方法的考查；有些问题学生可凭借数学直感、类比、归纳可以解决，考查学生的合情推理能力.台湾选择题一般客观性强，可信度高，具有较好的甄别和选拔功能.
特色2突出试题的现代数学背景
从台湾《普通高级中学数学课程纲要》可以看到，大学很多现代数学知识下放到了高中课程.台湾课程不但包括了大陆课程标准中的所有现代数学内容，而且还多了高次多项式函数、线性方程组、行列式与矩阵、向量的外积、空间中直线与平面的方程、极限、不定积分等.台湾大学入学考试命题以课程理念为指导，呈现出很多以现代数学为背景的试题.
例3（2013年“指考”数学甲单选题第4题）考虑所有由1、2、3、4、5、6各一个与三个0所排成形如0ab
c0d
ef0主对角线上的元素均为0的三阶方阵.今随机选取这样一个方阵，试问其行列式值0ab
c0d
ef0为奇数的机率为下列哪一个选项？
（1）120（2）110（3）12（4）910（5）1920
解将1，2，3，4，5，6六个数排a，b，c，d，e，f六个位置，有A66=720种方法.若要0ab
c0d
ef0=ade+bcf为奇数，则必须三个奇数1，3，5在一起相乘，三个偶数2，4，6在一起相乘，根据题设要求的排列方法有2A33A33=72种，则所求概率P=110，选（2）.
这个题呈现的现代数学背景有行列式、矩阵、概率.统计近五年的台湾高考题，概率与统计、平面向量、空间向量、极限、微积分、行列式与矩阵等现代数学内容是考试的重点，占分超过60%.
特点3试题贴近日常生活

《普通高级中学数学课程纲要》在“课程目标”中指出，培养学生具备实际生活应用和学习相关学科所需的数学技能.在“核心能力”培养中，提倡培养学生“连结能力”，能将课堂内学到的知识联系到生活实际，用数学知识有效地解决生活中随时可能碰到的问题.
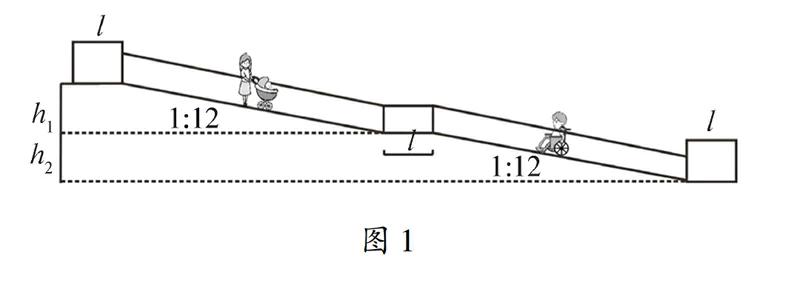
例4（2015年“指考”数学乙解答题第1题）根据内政部营建署《建筑物无障碍设施设计规范》，无障碍通路之设计需符合以下规定：
（1）坡道之坡度（高度与水平长度之比值）不得大于112；
（2）坡道之起点及终点，应设置长、宽各150公分以上之平台.此处的长指的是水平长度，而非斜面的长度；
（3）走道的中间应设置适当数量的平台，使得每段坡道的高差不超过75公分，且平台的水平长度至少150公分；
（4）各平台坡度不得大于150.
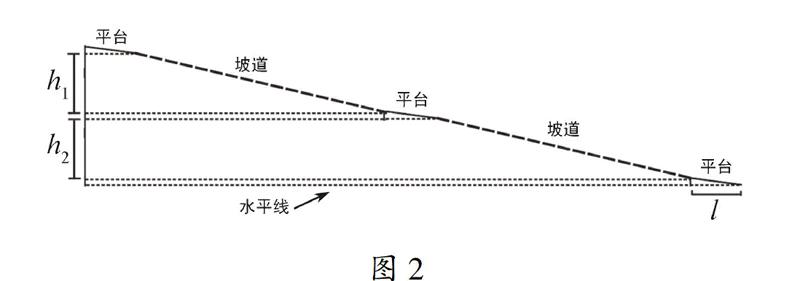
图1图2图1与图2为侧面示意图，图1摘自此规范书，图2为图1的简明版，其中l≥150，h1，h2≤75；走道之坡度相当于走道斜率之绝对值.
依上述规定，一条升高2公尺的无障碍走道，在无转弯的条件下，其最小可能的水平长度（含平台）为多少公尺？
解高度差为200公分，要有最短水平距离，则所有平台的坡度须恰好为150，且所有坡道的坡度须恰好是112，因为平台的坡度150小于坡道的坡度112，要得到最短水平长度就必须极小化平台的水平长度，也就是极小化平台的高度差.
每一个平台水平距离至少为150公分，也就是每个平台的高度差至少为150×150=3公分，可以观察：
当高度不超过6公分时，只能设计一个平台；
当高度差超过6公分，但不超过3+75+3公分时，可以设计前后两个各150公分的平台，中间一个坡道；
当高度差超过3+75+3公分，但不超过3+75+3+75+3公分时，可以设置前后两个各150公分的平台，中间两个坡道以及一个150公分的平台；
当高度差超过3+75+3+75+3公分，但不超过3+75+3+75+3+75+3公分时，可设置前后两个各150公分的平台，中间三个坡道以及两个150公分的平台；
四个150公分的平台会升高3×4=12公分，剩下的200-12=188公分的高度由坡道来提供，所以坡道的水平长度为188×12=2256公分，因此水平总长度为2256+150×4=2856公分，也就是28.56公尺.

这是一个生活气息很浓的数学试题，毫无人工编造的痕迹.统计台湾近五年的高考数学试题可以看到，这样“连结”生活实际的试题共有60多道.这不但是台湾试题的一大特色，更是一大奇观！真正让学生感受和理解到数学来源与生活，又将回到生活中解决实际问题.
特色4凸显能力立意的主旨
从例4还可以看到，题设文字表述多，但从求解过程看，没有繁杂的运算，也没用到特别强的数学技巧.这是台湾数学课本习题和重大考试数学试题的一种常见现象，练的和考的就是学生的阅读能力、理解能力、运算能力、写作能力.《普通高级中学数学课程纲要》特别重视学生数学能力的培养.因些，台湾高考数学试题突出能力立意的主旨，提倡试题能给学生提供多角度思考问题、一题多解的空间，反对试题求解过程中需要用到繁杂的运算和特别强的解题技巧.
例5（2015年“指考”数学甲解答题第二题）设无穷数列{an}符合a0=0且当n≥1时，an满足
综上，对一切大于等于0的整数n，不等式成立.故得证.
由{a2n}为严格递减，则当正整数n≥1时，a2n再由{a2n}为严格递减且limn→∞a2n=-18，得对任意正整数n，-18≤a2n，所以，-18≤a2n<0成立.
例5是2015年“指考”数学甲最后一个题，是一个综合性较强的试题，命题者把等比数列、极限、不等式等知识融入一题.第（3）小题求解中，可以从多个角度切入，做到一题多解.此题难度不大，不等式放缩的适度性也比较好把握，不需再用其他高超的解题技巧.
特色5与其他学科知识相互渗透
台湾数学教育非常重视学生“连结”能力的培养，即将数学知识与生活情境、其他领域、人类文化等连结，用数学方法去解决出现的问题.“连结”分5个阶段：察觉、转化、解题、沟通、评析.
例6（2015年“指考”数学乙多选题第4题）半导体产业的的摩尔定律认为“体积电路板可容纳的电晶体数目每两年增加一倍”.f（t）表示从t=0开始，电晶体数目随时间t变化的函数，并假设f（0）=1000.下面的选项中，请选出可以代表摩尔定律的公式：
（1）若t以年为单位，则f（t）=1000+10002t；
（2）若t以年为单位，则f（t）=1000+100024t；
（3）若t以年为单位，则f（t）=10002t；
（4）若t以年为单位，则
lgf（t）=3+lg32t+12；
（5）若t以年为单位，则lgf（t）=3+lg22t.
分析依题意知，f（2）=2000，f（4）=4000，f（6）=8000，…
用特殊值法可选出正确答案为（3）、（5）.
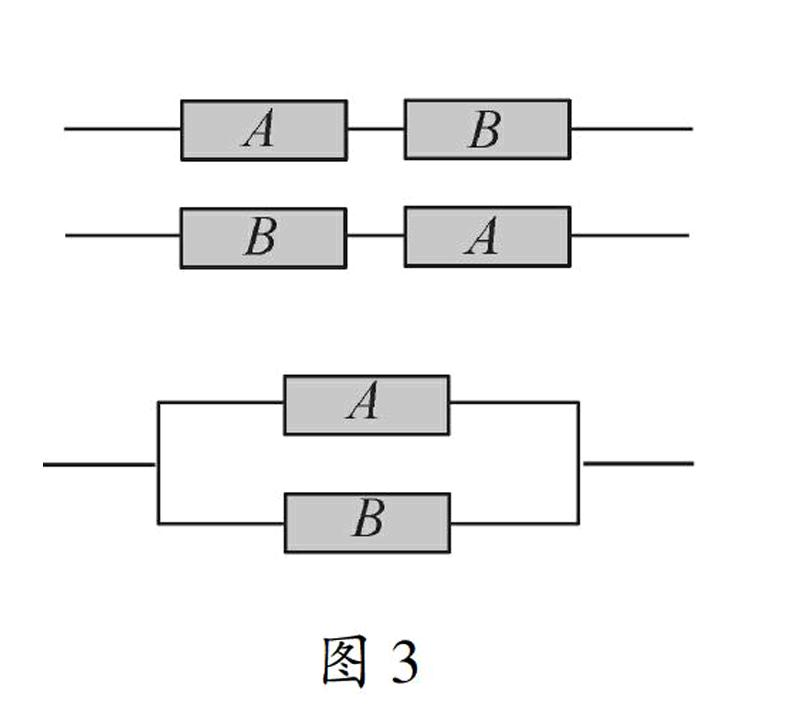
例7（2015年“学测”单选题第3题）有两组供机器运作的配件A、B，其单独发生故障的概率分别为01、015.只有当A、B都发生故障时，此机器才无法运作.A、B两配件若用串联的方式，前面故障会导致后面故障，但若后面故障则不会影响前面的故障；若用并联方式，则故障情形互不影响.若考虑以下三种情形：
（一）将B串联于A之后；（二）将A串联于B之后；（三）将A、B并联.
在情况（一）、（二）、（三）之下，机器无法运作的机率分别为p1、p2、p3.请选出正确的选项：
图3分析以题意画出三种情形相应的图像，如图3.在情况（一）下，机器不能运作的概率是p1=0.1，在情况（二）下，机器不能运作的概率是p2=0.15，在情况（三）下，机器不能运作的概率是p3=0.1×0.15=0.015.选（2）.
台湾数学教育倾向于培养学生数学工具化的意识，因此，他们淡化了以纯粹数学教学为主的数学教育，主张在数学与其他学科相互渗透的环境中学习数学.
特色6有机融入文化的元素
汪晓勤[1]、刘芳[2]等人的研究认为，数学文化的类型应分为数学史、数学与生活、数学与科技、数学与人文、数学与艺术体育、数学游戏等.台湾地区《普通高级中学数学课程纲要》也强调，引进与主题相关的数学文化，对学生会起正面的作用，尤其能协助学生将抽象观念具体化.因此，台湾大学入学试题也充分体现了这些课程理念.
图4例8（2014年“指考”数学甲选填题第B题）在游戏中，阿玲拿到如右的数字卡.主持人随机从1至9号球中同时取出三球，若这三球的号码中任两个都不在卡片上的同一行也不在卡片上的同一列时就得奖，则阿玲得奖的概率为（化成最简分数）.
分析符合题设要求的取法有3×2×1=6（种），
不考虑限制条件的取法共有
6+3×2×1+6C23×2+12×6×C23×4=84，
故阿玲获奖的概率是684=114.
例8是一个与数字游戏相关的问题，而且是一种常见的游戏.我们大家很小的时候都玩过.
从上文可以看到，台湾试题颇多特色，很值得我们学习、借鉴、欣赏.大陆高考数学试题无论是题型还是内容，几乎一成不变，显得过于刻板和无趣.我们应该学习台湾高考的命题原则和方法，试题编制要符合学生的认知能力，不要随意拔高或降低难度，避免偏题、怪题和难题.我们还应在高考试题中，增加多个有生活气息的应用题，让学生感悟到数学的实用价值和魅力.这样不但可以考查到学生观察、分析和解决问题的能力，还可以考查到学生阅读理解能力、数学建模能力，达到考试目标多元化的目的.
参考文献
[1]汪晓勤.主要国家高中数学教材中的数学文化[J].中学数学月刊，2011（4）：封底.
[2]刘芳.浙教版教材中数学文化渗透情况的分析[J].教学月刊（中学版），2010（3）∶24-28.
作者简介郝保国（1958—），男，湖南祁东人，数学高级教师；主要研究方向是课程、教材、教法、竞赛等；华南师大校外硕士生导师，广东省优秀教师；在《数学传播》、《中学数学杂志》等刊物共发表论文86篇，辅导学生获国际数学奥林匹克竞赛金牌1人次.

随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 9:21:56