网站首页  词典首页

请输入您要查询的论文：

　

标题 彩色图像压缩的量化编码方法研究
范文 杨树媛



摘 要：传统彩色图像三维离散余弦变换（3D-DCT）压缩体系中，量化器的设计没有充分考虑人眼视觉系统的影响问题，并且经典JPEG标准中的熵编码方法，存在码表太大、上下文模型难于创建的缺点。据此，提出了根据变换系数的概率分布构建的量化函数，并加入人类视觉系统影响因子；根据非零交流系数的非均匀分布，对于系数疏散区采用将Run和Level分别进行变长编码的新方法。该方法码表更简单，上下文模型更容易构造，在性能上有很大改进空间。实验结果表明，较JPEG在相同压缩比的情况下，PSNR可至少提高0.7dB，重建图像的主观质量也有很大改善。
关键词：三维离散余弦变换；图像压缩；熵编码
DOIDOI：10.11907/rjdk.151316
中图分类号：TP301 文献标识码：A 文章编号：1672-7800（2015）007-0030-03
0 引言
离散余弦变换（Discrete Cosine Transform，DCT）由于其较好的压缩性能，易于硬件实现和算法快速等优点，被广泛地应用于图像压缩等领域。三维离散余弦变换（Three Dimensional Discrete Cosine Transform，3D-DCT）被认为是运动补偿的替代算法。随着计算机硬件技术的发展，计算机运算速度越来越快，3D-DCT运算复杂耗时的问题逐渐得到解决。基于实际应用需要，其编解码复杂度一致，便于实时编解码的优势越来越突出。
量化是有损编码中的关键环节，一个好的量化，不仅要具有好的比特率-失真（Rate-Distortion，R-D）性能，还要具有好的重建图像主观质量。文献[1]研究了R-D最优量化器的设计方法；文献[2]研究了人类视觉对于高频系数不敏感而对于低频系数敏感的大体趋势，提出了据此设计3D-DCT量化器的方法；文献[3]提出了一种基于高斯概率分布函数来构造三维量化矩阵的新方法。
JPEG中对交流（Alternate Current，AC）系数进行熵编码的流程是：首先对AC系数进行游程编码（Run Length Coding，RLC），然后基于编码后的（Run，Level）统计特性进行霍夫曼编码（Huffman Coding，HC），这里Run指连续零系数的长度，Level是非零系数幅值的数量级。但采用该方法对连续的非零系数进行编码时，码流长度会增加，Tian[4]提出了对非零AC系数的密集区和疏散区采用不同编码方法的思路；在H.263中，Tu[5]提出对Run和Level分别进行编码。
本文针对彩色图像的三维离散余弦变换，依照交流系数的分布规律、人类视觉系统模型和三维Zigzag扫描特点进行量化器设计，并采用改进的将Run和Level分离可变长熵编码方法。试验结果验证了本文方法的有效性。
1 彩色图像三维模型和分块
一幅给定的M×N大小的彩色图像是由M×N大小的R、G、B三颜色分量的灰度图像组成，将颜色维视为第三维进行建模，则可以得到一个M×N×3的关于彩色图像像素值的三维模型。类似于JPEG，为了减少计算量，提高编解码速度，将M×N×3的三维模型统一分割为8×8×3的三维块分别进行3D-DCT。
2 量化
文献[6]研究发现，3D-DCT变换系数中，直流系数近似符合高斯分布，大部分AC系数符合伽马分布。根据3D-DCT系数的分布规律和量化器设计原理，本文提出了符合3D-DCT系数衰减规律的量化矩阵构造函数，如式（1）。
Q（i，j，k）=q×255（1-exp（-0.1（（i+1）+（j+1）+（k+1））））（1）
其中q为量化因子，通过调节q可以得到不同量化阶的量化值；i，j为8×8×3大小彩色图像三维块的水平和垂直位置，i，j=0，1，…，7；k为RGB颜色分量维的帧数，k=0，1，2。
根据人类视觉系统二维模型[7]，假设三维模型关于体对角线对称，将二维模型推广到三维空间，得出三维视觉模型H（i，j，k），如图1所示。
将经视觉因子加权后的量化矩阵构造为函数：
Q′（i，j，k）=Q（i，j，k）H（i，j，k）（2）
根据文献[3]提出的分区域量化思路，对于不重要区域的系数进行大尺度量化，结合本文采用的三维Zigzag扫描方法特点，避免扫描后存在游弋系数的现象（即因量化造成的，在大部分零区域内出现个别非零AC系数的情况），以i+j+k=C函数作为区域分割线，其中C为一常数。当在此界限内时，即i+j+k≤C，为重要系数区域，用前文设计的量化器进行量化；反之则为零区域。另外，根据压缩倍数越大时，量化尺度越大，零区域的范围就会越大，重要区域的范围就越小的特点，取C=α/q，其中α为阈值因子，为一常数，q为式（1）中量化因子，则零区域的判别公式如式（3）。
f（i，j，k）=0 （i+j+k>α/q）（3）
3 熵编码
直流系数的熵编码方法和JEPG一致。对于AC系数编码，本文采用对Run和Level分别单独编码方法，易于上下文模型的构造以进一步提升性能。假设基于（Run，Level）的JPEG码表开销是R×L，文中方法仅为（R+L）。码表如表1所示，编码形式如下：
（Run）B（Level）B（Amplitude）B
其中，（Run）B和（Level）B分别是Run和Level对应的二进制码字。（Amplitude）B为非零AC系数幅值对应的二进制码字，编码方法和JPEG一致。
JPEG中只提供了游程长度不超过15的霍夫曼码表，当游程长度大于15时，用（15，0）表示16个连续的零，采用一个或多个（15，0）及剩余的游程和非零AC系数的类别组合来进行熵编码。
不同于JPEG的8×8个量化系数中很少有游程长度超过15的非零AC系数，3D-DCT的三维块有8×8×3个系数，游程长于15的概率大大增加。本文采用文献[8]中提出的改进熵编码方法，对游程超过15的情况进行编码。
假设有一个集合{an}，其值为12，14，18，…，12n，其前N个数的和为 （Sn），计算如下：
Sn=a1+a2+…an=121-12n1-12=1-12n（4）
当n→∞，Sn的极限是：
limn→∞Sn=limn→∞1-12n=1（5）
根据非零AC系数的分布，游程编码后，Run不变，随着Level的增大，（Run，Level）数对出现的概率逐渐降低。假定同一Run，不同Level的（Run，Level）的概率为{an}。当Run为k时，定义编码采用JPEG的平均码长λk和本文方法的平均码长λ′k如下：
λk=λ1a1+λ2a2+…+λnan（6）
式（6）中，an和λn分别是Level为n时， （k，n）数对出现的概率和对应JPEG编码的码长。
λ′k=λ′1a′1+λ′2a′2+…+λ′na′n（7）
式（7）中，a′n和λ′n分别是Level为n时， （k，n）数对出现的概率和本文方法编码对应的总码长。
JPEG和文中方法的平均码长对比如表2所示。可以看出，当游程长度大于5时，本文方法具有明显优势。根据非零AC系数密集区的游程一般较短，疏散区的游程较长的特点，对于密集区采用JPEG编码方法，疏散区则采用本文提出的编码方法。
由于疏散区和密集区的最佳分割位置不是本文研究重点，文中将前8个非零AC系数视为密集区系数，采用JPEG编码，其余系数采用文中方法编码。为了便于解码，块结束标志位（End Of Block，EOB）被视为分割位置的标识，其表示一种熵编码方法的结束和另一种熵编码方法的开始。
4 仿真结果与分析
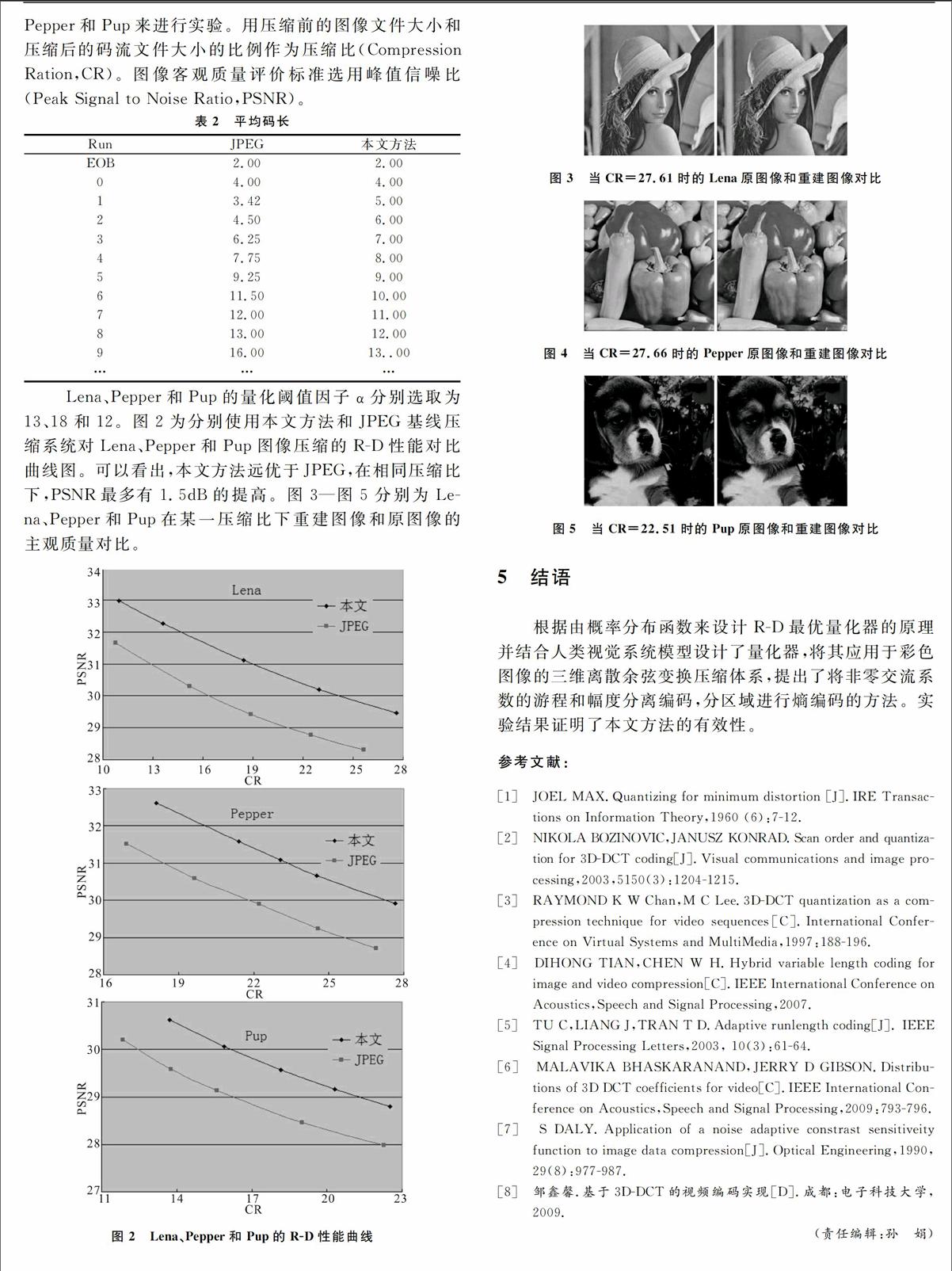
选用256×256大小的24位彩色标准测试图像Lena、Pepper和Pup来进行实验。用压缩前的图像文件大小和压缩后的码流文件大小的比例作为压缩比（Compression Ration，CR）。图像客观质量评价标准选用峰值信噪比（Peak Signal to Noise Ratio，PSNR）。
Lena、Pepper和Pup的量化阈值因子α分别选取为13、18和12。图2为分别使用本文方法和JPEG基线压缩系统对Lena、Pepper和Pup图像压缩的R-D性能对比曲线图。可以看出，本文方法远优于JPEG，在相同压缩比下，PSNR最多有1.5dB的提高。图3—图5分别为Lena、Pepper和Pup在某一压缩比下重建图像和原图像的主观质量对比。
5 结语
根据由概率分布函数来设计R-D最优量化器的原理并结合人类视觉系统模型设计了量化器，将其应用于彩色图像的三维离散余弦变换压缩体系，提出了将非零交流系数的游程和幅度分离编码，分区域进行熵编码的方法。实验结果证明了本文方法的有效性。
参考文献：
[1] JOEL MAX.Quantizing for minimum distortion [J].IRE Transactions on Information Theory，1960 （6）：7-12.
[2] NIKOLA BOZINOVIC，JANUSZ KONRAD.Scan order and quantization for 3D-DCT coding[J].Visual communications and image processing，2003，5150（3）：1204-1215.
[3] RAYMOND K W Chan，M C Lee.3D-DCT quantization as a compression technique for video sequences[C].International Conference on Virtual Systems and MultiMedia，1997：188-196.
[4] DIHONG TIAN，CHEN W H.Hybrid variable length coding for image and video compression[C].IEEE International Conference on Acoustics，Speech and Signal Processing，2007.
[5] TU C，LIANG J，TRAN T D.Adaptive runlength coding[J]. IEEE Signal Processing Letters，2003， 10（3）：61-64.
[6] MALAVIKA BHASKARANAND，JERRY D GIBSON.Distributions of 3D DCT coefficients for video[C].IEEE International Conference on Acoustics，Speech and Signal Processing，2009：793-796.
[7] S DALY.Application of a noise adaptive constrast sensitiveity function to image data compression[J].Optical Engineering，1990，29（8）：977-987.
[8] 邹鑫馨.基于3D-DCT的视频编码实现[D].成都：电子科技大学，2009.
（责任编辑：孙 娟）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/5 22:13:46