《让几何画板在数学课堂中大放光彩》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

让几何画板在数学课堂中大放光彩

范文

鲍慧

【摘要】几何画板使以往的数学教学由老师单凭讲、写、练进行教学的模式上升为现代化的多媒体教学模式.它把教师对课堂教学的设计思想、步骤、方法和学生的参与与软件本身有效地结合起来，并通过软件得到完美的表现.其体现的并不仅仅是教师的计算机软件技术水平，而是教学思想和教学水平.笔者结合自身的教学实践谈谈几何画板在高中数学教学中的应用和使用建议，供参考.

【关键词】几何画板；数学；教学

一、在教学中的应用

新课标认为：“应重视信息技术与数学课程内容的有机整合……教师在教学中应予以关注.信息技术与数学课程内容的整合还有较大空间，教师可以在这方面进行积极的、有意义的探索……现代信息技术的广泛应用正在对数学课程内容、数学教学、数学学习等方面产生深刻影响.在教学中应重视利用信息技术来呈现课堂教学中难以呈现的课程内容……提倡信息技术与课程内容的有机整合，整合的原则是有利于学生认识数学的本质.从而改变学生的学习方式和教师的教学模式.”

从上述表述可以看出，“整合的基本原则是有利于学生认识数学的本质”，整合应该紧紧围绕这一基本原则进行，应当尽可能地向认识数学的本质这一深层次迈进，而不是停留于表面和形式.结合目前的教学实践，笔者就常见的“以往课堂教学中难以呈现的课程内容”中的函数图像、点的轨迹进行例析.

（一）函数图像的探索不再困难

我国著名数学家华罗庚说：“数缺形少直观，形缺数难入微.”这句话不但深刻地揭示了数学中数与形之间的相互依存关系，而且还体现了辩证唯物主义思想.数形结合是高中阶段重要的数学思想，将其贯彻于数学教学过程始终，是教好数学的关键之一.

函数在中学数学中的地位十分重要，解析式和图像之间常常需要对照加以记忆.缺乏信息技术支持的数学课堂往往只能截取函数图像的几个特殊画面，函数图像的变化过程只能用语言进行描述.这样的结果通常是教师讲得口干舌燥，学生听得一头雾水.应用几何画板则可以克服上述种种弊端，大大提高课堂教学效率，从而达到事半功倍的效果.

例1探究参数A，w，φ对函数y=Asin（wx+φ）图像的影响.

传统教学中教师只能通过将A，w，φ取几个值，然后进行手工绘图，让学生观察图像之间的关系，这样不仅耗时长而且往往达不到预期的教学效果.利用几何画板则可以用三条线段的长度控制函数的振幅、周期和频率等参数的变化，制作成课件，教师进行演示或者让学生亲自动手操作，在动态的演示中轻松地学会所学知识.

（二）发现疏忽和错误显得轻而易举

根据数形结合思想画出草图是常见的解题方法，但画草图时如果图形严重失真，可能会得到错误的答案.利用几何画板可以画出非常精准的图形，必要时还可以将图形放大，获得更精细的图像，帮助学生发现解题过程中的疏忽和错误，并引导学生进一步思考错解的原因.

例2求方程x2=2x的解的个数.

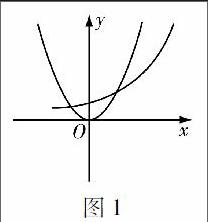
错解画出函数y=x2和y=2x的草图（见图1），由图可知，有2个交点.故原方程有两个解.

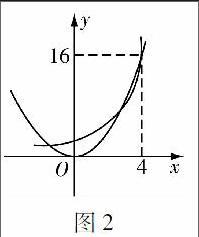
正解用几何画板画出精确的图形（见图2），可以清楚地看到还有一个交点（4，16），所以原方程有3个解.反思错解的原因是画图失真，而且没有考虑到函数y=2x的指数爆炸性增长的特点，因而漏解.

（三）探寻点的轨迹不再那么神秘

点的轨迹问题，一直以来都是学生较难理解和掌握的问题，大多数学生绞尽脑汁，其结果往往也是一头雾水，手工画出其草图，又不能保证其所画图形的精确性，尤其是对初学者来说，更难以形成自己的知识，达不到熟练应用的程度.如果应用几何画板，就可以以动画功能描绘出轨迹的形成过程，使学生能够容易地抓住其本质进行学习.

最近，笔者开了一节题为“双曲线及其标准方程”的展示课，采用几何画板展示“平面上到两个定点的距离的差的绝对值等于常数（小于两定点间的距离）的点的轨迹”，该过程形象生动，很好地展示了动点轨迹的形成过程，取得了较好的教学效果.

二、使用建议

（一）适度使用

作为数学教师，应当改变观念，与时俱进，不以种种理由排斥在教学中使用信息技术.同时，教师在信息技术与数学课程的整合过程中，应当根据数学学科的特点探索如何将信息技术有效地融合于数学教学的过程，即根据具体的数学教学内容，适时且适度地使用技术，实现数学教学最优化和最高效.另一方面，教师还应该注意避免过度使用技术，不忽视纸笔运算，不忽视与学生之间的互动交流.

（二）自己动手

网络上有大量优质的教学资源，教师应当善于利用這些网络资源.但是他人的东西往往只能借鉴，未必就完全适合于自己的学生，也未必能够体现自己的教学设计思路，因此，必要时，教师还是要自己制作课件.笔者认为只有自己做的课件，用起来才更得心应手，教学效果才更好.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。