《债券持有期收益率，久期及在险价值计算和分析》-经济学论文，金融论文-论文范文参考-科学狗论文网

标题

债券持有期收益率，久期及在险价值计算和分析

范文

杨伟杰

摘要：债券投资最近几年慢慢引入个体投资者的视线之中。随着中国刚性兑付制度取消，债券投资的违约组合管理变得至关重要。而个体投资者因为债券投资专业要求而占有整体的少部分。本文通过使用python计算机语言作为工具，提供持有到期收益率，考利久期，以及风险指标VaR（在险价值）的计算方法。为投资者提供债券分析的简便方法。

关键词：债券YTM? 麦考利久期? VaR? Python

一、持有到期收益率，麦考利久期及在险价值

目前，债券投资主要以机构投资者为主，个体投资者属于少数前提，主要是由于债券投资对于专业知识的要求比较高，其收益率的计算，久期管理，VaR计算对个体投资者要求较高，其实通过python的数据处理可以处理流动性较高的债券收益率，久期和VaR的计算。首先在通过python实现上述计算，需要了解债券的一些基本要素，分别是：债券面值，附息利率，附息频次，债券存续时长，债券现值，发行主体。本文主要关注前五个要素。其中假设债券持有到期，其持有到期收益率并不是附息利率，需要通过上述五个要素进行计算才能知道投资者的回报率。而债券的现值（即债券的每日收盘价）在不断变化，因此其收益率也在不断变化。针对折价，溢价，平价发行的债券其收益率变化也会不同。通过python则可以完成持有到期收益率（YTM）的计算。为投资者选择债券提供一些指导。

在完成债券的YTM计算后，则可以继续计算麦考利久期。麦考利久期是债券投资中的重要工具，它的数值可以反映投资者的债券投资现金流平均的回流时间;其次久期很好的反映了债券价格对应利率变化的敏感度，并且通过债券的久期的管理可以對债券组合的杠杆进行很好的管理。在本文中，可以通过python很快的进行麦考利久期的计算，从而方便投资者进行债券投资的进一步分析以及债券池的管理和存续。

最后，VaR指标的全称为Value at Risk（在险价值），由摩根大通提出，是指在一定的时间内，一定的置信度下，投资者最大的期望损失。本文利用python通过历史模拟法一步得出不同置信度下的VaR，帮助投资者更好的进行债券投资组合的管理。对于风险超过投资者能力的债券及时止损，达到初步控制风险的作用。

二、 Python在本项目中的作用及项目逻辑

首先第一部分，在YTM计算部分，python通过datatime模块进行附息日和债券现值日期差的确定，从而确定每笔附息日的折现时长;其次利用循环语句根据选定时间内的债券收盘价，通过公式运算求得YTM。

其次，在得到利率曲线后，通过python中的基础运算，写出久期公式，并通过dataframe的形式导入源数据，按照次序循环带入公式，得到债券在不同收盘日的麦考利久期。

最后直接利用python的quantile函数和绘图模块得到不同置信度下的VaR。至此完成整个项目，得到YTM，麦考利久期和VaR三个数据。

三、债券选择：债券持有到期计算——基于python- dataframe、datatime模块

在债券市场中，以流动性较好的债券为例，其债券价格在不断的变化，而债券的附息利率并不等于其真实收益率。以债券代码：113526（联泰转债）为例，通过python对债券数据的爬取，并进行计算，可以获得该债券在每天收盘时的持有到期收益率。

首先通过python获取该债券的源数据的csv文件，通过python以dataframe的形式读取该文件。其中该数组的第一列为日期。债券的持有到期收益率公式如下：

该债券的存续日期为6年，面值100，并且每年的附息利率不相等。其中pv作为每日的收盘价进行变化从而影响YTM的变化。计算YTM之前，先要确定附息日距离当日收盘日的天数差距（以年化记录）从而确定所有分母的幂。

通过下面的代码，可以确定债券在每年的附息日点和当前债券现值的收盘日之间的天数差值，求得天数差值后，通过append函数添加到列表中，保存起来。在编写公式时，将所求的天数差进行年化（除以365天），然后带入公式，使用Sympy函数来求解高次方程，即可得到每个交易日下的持有到期收益率的具体数值。

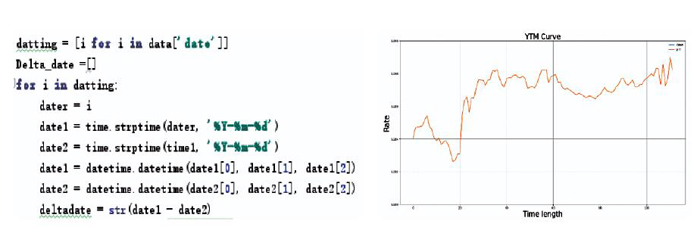
在得到数据后，通过使用matplotlib绘图函数来探索YTM的图像便于分析。从下图中我们可以看到，债券的持有到期收益率在3.5%附近。债券的持有收益率之所以维持在较低水平，是因为该债券是可转债，债券持有者具有在未来时刻将债券按照一定比例转化成股票的权利。该权利归属于投资者，因此债券发行方通过降低债券的收益率来弥补投资者获得的相对优势。如果移除债转股的特性，这只债券的收益率将会出现进一步的上升，因为债转股特性对债券持有者有利，作为移除该权利需要对投资者进行溢价补偿。

其次，观察该债券的持有期收益率的走势，可以发现是逐步下降的（横坐标轴时间线降序排列），主要是因为其债券价格从截取时间段的初始值102元上升到了138.38元（结束值）。从上述的公式中我们可以发现债券的价格和持有到期收益率呈负向关系。因此实际计算得出的数值和理论公式中的数值是趋于一致的。

四、债券存续管理：麦考利久期计算——基于python函数计算模块

在获得债券的YTM后，我们需要建立债券现值与利率之间的联系。麦考利久期能够很好反应两者变化的敏感度。首先先给出麦考利久期的计算公式：

观察公式我们发现分子部分是债券价格变动的百分比，分母部分是利率变动的百分比。通过公式可以大致理解其意义：债券价格对利率变动的敏感度。麦考利久期越大，说明越敏感，利率变动会引起债券价格变动幅度更大。在这里，使用python的循环语句我们可以快速的计算出麦考利久期，并且在处理数据时要注意一些极端异常值及时剔除，以免影响判断。

并且利用matplotlib的绘图功能，同样可以对麦考利久期的变化进行直观的分析。总体来说，债券的麦考利久期越大，说明现金流的平均回流时间越慢。由于其每日的收盘价格并不是完全由市场利率来决定，市场参与者的买卖行为也会应该债券的现值，并且麦考利久期假设利率平行移动，但是很显然，真实市场上的投资利率并非平行移动。因此从图中可以观察出这只债券的麦考利久期波动变化十分剧烈，主要是由于其分子——债券价格的剧烈变化导致了其久期的剧烈变化。在以久期作为债券池管理手段时，针对波动比较剧烈的债券，我们可以观察久期的分布情况，平均数，众数等方式来获得更加有用的麦考利久期方面的信息。

除去麦考利久期之外，还有修正久期，美元久期，关键利率等其他种类的久期也可以使用python进行编写来进行进一步的数据处理。在这里只介绍麦考利久期。

五、风险管理：在险价值计算——基于python-quantiles函数及matplotlib模块

在完成债券的久期管理及计算之后，最后一步也至关重要，使用VaR进行债券的风险管理。本文采用简单的历史模拟法，即对历史数据进行排序，通过不同置信度下进行切割，得到投资者在某个时间段内某个置信度下的期望损失。为投资者提供止损的指导。

在python中，主要使用quantiles内置函数计算VaR，再通过matplotlib模块来直观绘制VaR图像，帮助投资者做出合适的决策。

上图代表的是这只债券在歷史模拟法下的在先价值，图中的黑色虚线代表的是在95%的置信度下的VaR。投资者在给定时间段内的95%置信度下的期望损失。当投资者的实际损失逐步逼近黑线甚至超过黑线时，需要提升警觉，甚至准备卖出债券以止损。当投资者的投资损失未靠近或触及黑线时，则说明该债券在投资者定义的风险承受能力下处于安全地带，可以继续持有。对于不同投资者对风险的态度，还可以设置99%，90%，99.99%等不同置信度，使得结果更加严格，提高风险控制的门阀。本文主要以历史模拟法得到该债券的在险价值。历史模拟没有分布假设，在数据量大时精度会提升。若数据量较小时可以使用参数法或者蒙特卡洛模拟等发放来绘制VaR曲线。

但是VaR也有不足的地方，VaR作为谱风险的一种特殊性，在95%的分位点赋予了100%的权重，其实并没有考虑尾部的极端风险。从上图中我们可以看，黑色虚线的左侧部分其实出现了一个很小的高峰，而VaR并不能反映该风险。因此，若投资者更加关注尾端风险，可以使用Expected Shorfall（损失期望值）来更好的反应尾部的极端风险。

六、总结

对于投资者而言，债券投资和股票投资占据了金融市场上的大部分份额。而无论是投资标的的选择，还是标的存续期管理，两者所要求的专业知识和技能是不同的。就债券而言，在选择初始标的时，需要关注债券的持有到期收益率，麦考利久期，债券的评级，发行主体，附息利率等等作为选择标的的信息指标，其中发行主体和评级十分重要，主要是因为债券存在违约的可能性。其次，若投资者持有多个债券时，针对整个债券池的管理和股票池的管理方式也不太相同。债券组合中久期管理和VaR管理显得尤为重要。债券组合的市值变动往往表现出对利率的负相关性，通过久期可以很好的衡量两者的敏感度，若投资者更加追求精度，则可以使用凸度来进行债券价值变动的更好拟合。总体来说，上述提到的指标和管理方法可以使用python作为工具进行计算来提升效率，缩短指标的计算时间，从而能够为投资者及时提供持有标的的综合情况，便于投资者做出投资决策。

参考文献：

[1]拉尔夫·吴.收益率曲线、久期与套息收益. 金融市场研究，2017（08）：11-21.

[2]Homaifar，Michello.A generalized algorithm for duration and convexity of option embedded bonds. Applied Economics Letters，2019：835-842.

[3]王禹辰.基于VaR的可转换债券市场风险的度量.时代金融，2017（03）：251-258.

[4]敬志勇，王周伟.信用评级、债券久期与投资者判断分歧.金融经济学研究.2014（06）：29-38.

作者单位：上海大学

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。