《基于深度学习探索小学数学的有效说理》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

基于深度学习探索小学数学的有效说理

范文

张萍萍

【摘? 要】伴随着新课程改革的深入，要求教师有效研究课堂教学策略，深入挖掘教材，深度理解小学数学中的说理能力，给学生创造说理的机会，运用合理的问题引导学生，让学生主动表达想法，为学生提供一个更广阔的说理空间。

【关键词】小学数学教学;说理能力;培养策略

中图分类号：G623.5? ? ? 文献标识码：A? ? ? 文章编号：0493-2099（2021）06-0064-02

【Abstract】With the deepening of the new curriculum reform， teachers are required to effectively study classroom teaching strategies， dig deep into teaching materials， and deeply understand the reasoning ability in elementary school mathematics， to create opportunities for students to reason， use reasonable questions to guide students， and let students actively express their ideas，Provide students with a broader space for reasoning.

【Keywords】Elementary school mathematics teaching; Reasoning ability; Training strategy

加强小学数学说理能力的深度学习，就是让学生通过听、说、看、做等各种途径学习，体验新知形成的过程并主动获取与灵活运用新知。这样培养学生的说理能力，让学生在不断探究中找到知识之间的联系和发展的规律，让学生体验每一个说理的过程，真正实现深度学习。

一、说理，提升知识内涵

数学知识体系不是一个个概念、一块块知识的简单组合，而是一个具有内在联系的逻辑结构系统。把握数学知识的内在联系与解析，让学生对所学知识进行充分说理有利于学生把数学知识结构内化为自己的认知结构，提升学生的综合能力和数学内涵。

乘法分配律是小学数学中非常重要的运算律。在教学中，让学生从现实生活中抽象出乘法分配律的“形”，初步感知构建模型。然后透过乘法分配律外在的“形”，深入研究乘法分配律内在的“神”。如：简算89×199，让学生自由发挥乘法分配律的“神”，从而使计算简便。学生言之凿凿，此时出现两种声音：

1.把199看作200-1，再运用乘法分配律。89×（200-1）=89×200-89=17711。

2.把89看作90-1，再运用乘法分配律。（90-1）×199=90×199-199=17711。

你更喜欢哪种算法呢？答案尽在不言中。言之有理，答案立现。说理，引导学生对抽象的知识模型进行解释和运用，引领学生感悟学习中蕴含的逻辑思维和数学内涵。

二、说理，发展深度思维

数学是思维的体操。数学思维与说理能力有着密切的关系，数学思维建立在数学说理的基础上，数学说理使数学思维更有深度。有效说理是训练数学思维的一种常用方式，课堂教学中，教师让学生对解题思路进行有效说理，全面展示数学思维过程，有助于深化知识，挖掘学生有价值的思维，真正实现数学的深度学习。

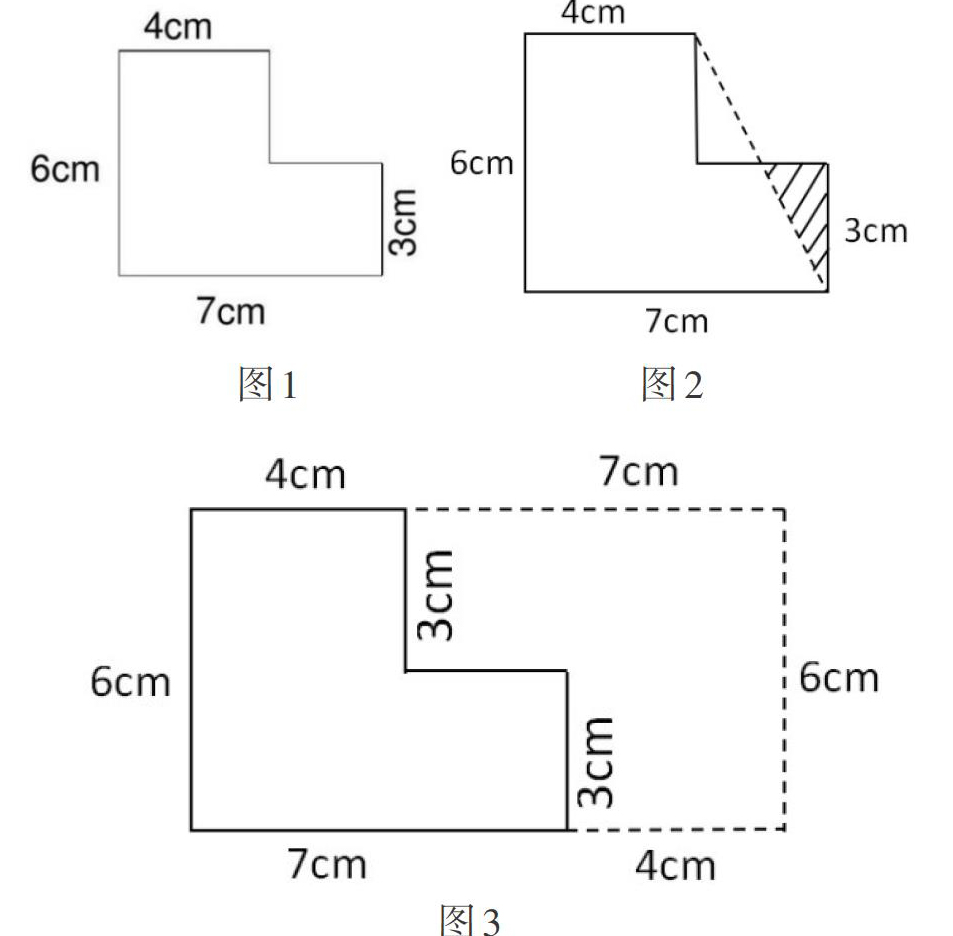
在教学“组合图形的面积”一课中，有一例题如图1，在学生尝试用分割法和添补法计算出组合图形的面积后，教师提出一个问题：“昨天晚上我在备课时，我儿子给了我一个这样解答的算式：（4+7）×6÷2。这个算式你们看懂了吗？”话音刚落，学生异口同声地说：“老师，我懂！”一学生边画边说（如图2）：如图画一条辅助线，把下面阴影的三角形割补到上面空白的三角形，这样就变成一个梯形，所以列式为（4+7）×6÷2。教师又补充道：“可我儿子又说了两个字‘复制，这次你们看懂了吗？”“我懂！”又一学生边画边说（如图3）：如图3“复制”一个图形，这样两个图形可以拼成一个长方形，所以列式为：（4+7）×6÷2。在实际教学中，教师要创设合理的时机，让学生有理必说，充分表达自己的见解，鼓励学生在解法上求新求异，既符合各层次学生的认知需求，又有利于学生深入理解知识，提高解题技巧，促进学生思维的深度发展。

三、说理，领悟数学思想

德国数学家莱布尼兹指出：数学的本质不在于它的对象，而在于它的思想方法。数学的基本思想是新课程标准提出的“四基”之一。美国教育心理家布鲁纳指出：“掌握基本的数学思想方法，能使数学更易于理解和更利于记忆，领会基本数学思想方法是通向迁移大道的‘光明之路。”因此在教学中，教师要有意识地渗透一些基本数学思想方法。在学生体验知识的形成过程中，让学生充分表达想法，解析说理，很自然地渗透数学思想方法。如：教学“有几瓶牛奶——9加几”中，9+5=（）你是怎么算的？让学生用小棒摆一摆。学生说出各种算法，教师加以肯定，然后重点讲解“凑十法”的计算方法和道理。教师：为什么只移动1根过去？不移2根、3根呢？学生：移动1根过来，这边正好凑成10根（一盒牛奶）。教师：那为什么凑成10个呢？学：10加几比较好算。教师：像我们课前的口算题一样，能很快地算出得数。在这一教学环节中，教师通过一系列的质疑，让学生结合实际操作形象、直观、循序渐进地进行说理，有效地落实数学思想（转化思想）的渗透，使学生真正有所领悟。

又如教学“平行四边形的面积”时，先让学生联想、猜测：“长方形的面积与它的长和宽有关，请同学们猜测一下平行四边形的面积和什么有关？有什么关系？”这一环节的目的是激发学生去进行验证，然后學生动手用学具剪一剪，接着同桌交流，学生争先恐后地说出验证方法。在学生说出几种转化方法后，教师追问：这几种方法有什么共同的地方？为什么沿高剪开？学生：长方形有四个直角，只有沿高剪开，拼时才能出现直角。最后讨论：拼出的长方形和原来的平行四边形相比，你发现了什么？结合图形的转化过程再进行一次完整的描述推导的过程。这样学生不仅知其然，而且知其所以然，让学生在充分的验证中说理，真正领悟数学的思想方法。数学思想方法是数学的灵魂，实际教学中，教师有意渗透，让学生学会用数学思想方法提出问题、分析问题、解决问题，让学生的有效说理切实得到发展。

四、结语

总之，在教学中，让学生用准确、精练、清晰、完整的语言表述观察过程、操作过程、算理算法和解题思路，长此以往，既能加深学生对知识内涵的理解，又能促进学生思维能力的深度发展，还能形成一定的数学思想方法。培养学生有效的说理能力任重而道远，必须持之以恒，让学生快乐说数学，“说”出胆量，“说”出本领，“说”出口才，“说”出智慧。

参考文献：

[1]何忠师.引导学生把握数学知识的内在联系[J]. 安徽教育科研，2003（01）.

[2]丁秀芬.为什么说“数学是思维的体操”——小学数学思维训练的方法分析[J].中华少年，2018（14）.

[3]刘强.课堂教学应如何关注数学思想方法[J].语数外学习：数学教育，2014（11）.

[4]林碧珍.数学思维养成课：小学数学这样教[M].福建：福建教育出版社，2013.

（责任编辑? 李? 芳）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。