《利用极坐标计算二重积分的一个简单推广》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

利用极坐标计算二重积分的一个简单推广

范文

范三妞秦玉鹏

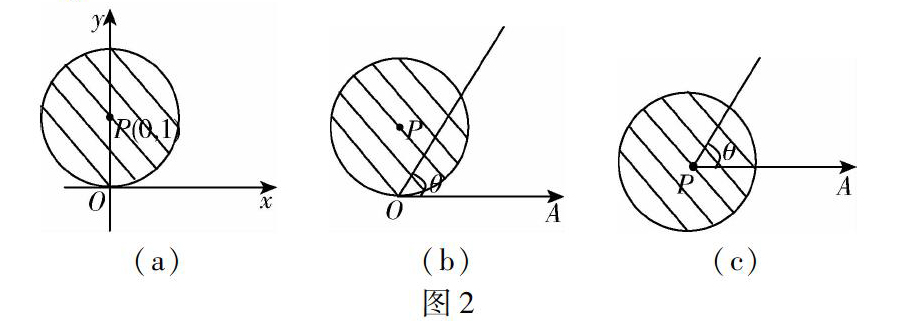
【摘要】在利用极坐标计算二重积分时，现行教材的极点通常选定为坐标原点，本文将极点从坐标原点推广到任意点，应用极点在任意点处的极坐标变换公式，给出了此极坐标系下二重积分化为二次积分的公式.结合具体算例将原公式和推广的公式进行对比，发现后者对某些关于非原点对称的积分区域情形更易计算，并讨论了两类极坐标系的选择标准.

【关键词】极坐标;二重积分计算;极点位置;积分区域对称性

一、引言

二重积分是高等数学的重要内容之一，根据被积函数和积分区域的不同可选择不同的计算方法和技巧[1-3]，其中应用极坐标计算二重积分更是教学中的重點和难点.现行教材中往往选择坐标原点作为极坐标系的极点，而对关于非原点对称的积分区域，选用该极点就不能充分利用对称性来简化做题过程.为了克服上述问题，本文的主要目标就是将极点从坐标原点推广到任意点，给出对应的极坐标计算公式.

二、极点在坐标原点的情形

本部分将简要回忆并给出极点在坐标原点时，利用极坐标计算二重积分的若干定理和公式，以便后文的推广和对比.

通过比较例3的两种解法，不难发现：虽然方法2的累次积分中关于ρ的积分限与θ无关，但是鉴于被积函数的形式，使得关于ρ的积分很难计算，即使笔者借助符号计算软件Maple也很难计算出结果.

那么对关于非原点对称的积分区域情形，究竟选用何种极坐标系进行计算更为简单呢？综合上述三个例子，不难总结出计算时应综合考虑如下两点：

（1）经过极坐标变换后的累次积分中，关于ρ的积分限是否与θ有关;

（2）经过极坐标变换后的累次积分中，被积函数对ρ是否容易积分.

据此可给出如下标准：

（1）若经过极坐标变换后，关于ρ的积分限与θ无关，被积函数对ρ容易积分，则理论上选用积分区域对称点作为极点的极坐标计算公式更为简单，如例1、例2;

（2）对其他情形，则应综合考虑计算量和计算难度后再做选择，如例3.

五、结论

针对应用极坐标计算二重积分的公式，本文将极点从坐标原点推广到了任意点处，并给出了对应的极坐标计算二重积分的公式.通过与原公式对比，给出了应用极坐标计算需要考虑的两点因素，并指出推广的公式对某些关于非原点对称的积分区域情形更易计算.

【参考文献】

[1]潘志.分部积分法在二重积分中的应用[J].工科数学，1993（4）：192-193.

[2]汪秀羌.二重积分的对称性问题[J].工科数学，1996（4）：181-184.

[3]刘继成，王湘君.反常二重积分收敛性的判定[J].大学数学，2015（3）：53-59.

[4]同济大学数学系.高等数学（下册）：第7版[M].北京：高等教育出版社，2014：147-160.

[5]黄冶文.二重积分的计算与应用[J].数学学习与研究，2017（7）：4-7，9.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。