在高中物理教学改革的今天，教学大纲重视开发学生大脑右半球的优势，发挥其直觉、预感与技能，增强学生解答物理问题的时间速度性与准确性，及时进行反馈，正确运用强化方法.教学在理解物理概念前提下，建学习目标，开发动力，注重养学生超越逻辑分析的思维能力，促进学生积极排解问题干扰，克服学习困难，努力强化分析问题技巧.在机械能知识点学习过程中，经常涉及到物系的速度关系.在这方面，速度约束关系上往往许多同学会产生疑惑，本文加以阐述.
1 接触型约束
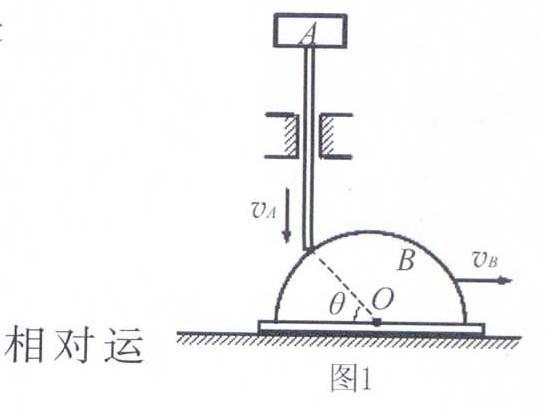
例1 如图1所示机械传动机构，当连杆系统A在轴套中竖直移动时，下部接触的半圆柱体随之水平移动.设连杆与半圆柱体的接触点和圆心O的连线倾角为θ时，连杆A的速度为vA，半圆柱体的速度为vB，则下列关系式正确的是
A.vA=vBsinθ
B.vA=vBcosθ
C.vA=vBtanθ
D.vA=vBcotθ
解析 方法一 相对运
动法
连杆下端点相对水平面的运动速度vA，等于该点相对半圆柱体的速度u与半圆柱体相对水平面的速度vB的矢量和.而连杆下端点相对半圆柱面的速度u沿圆的切向，作出速度矢量关系如图2所示，故得：
vA=vBcotθ
方法二 速度分解法
连杆下端点与半圆柱面始终紧密接触，故垂直接触面方向的分速度（即圆柱面半径方向的速度）始终相等，如图3所示，故有
vAsinθ=vBcosθ
即vA=vBcotθ
答案：D
点评 对接触物的接触点，速度关联的特征是：沿接触面法向的分速度始终相等，而沿接触面切向分速度不一定相等（当有相对滑动时）.接触点的关联速度也可用相对运动规律求解.
2 涉及关联速度的物系动能问题例析
例1 如图4所示，质量为m、摆长为L的单摆竖直悬挂时，摆球刚好与放在光滑水平面上的斜劈M接触，斜劈的倾角为θ=53°，斜面光滑，质量也为m.现由静止开始，用F=mg的水平恒力向左推斜劈，到摆线与斜面平行时，摆球的速度多大？
解析 如图5所示，设斜劈推至摆线与斜面平行时，斜劈M的速度为v1，位移为s1，摆球的速度为v2，对系统，根据动能定理，有
Fs1-mgL（1-sinθ）=12mv21+12mv22
题设 F=mg，
斜劈的位移为s1=Lcotθ=Lcot53°=34 L
难点在求二者的关联速度，有两种方法：
方法一 相对运动法
摆球相对水平面的速度v2，等于摆球相对斜面的速度u与斜劈相对水平面的速度v1的矢量和.如图6所示，图中v2垂直摆线，摆线平行于斜面，故
v1sinθ=v2
θ=53°，v1=54v2
方法二 速度分解法
利用摆球和斜劈二者在垂直斜面方向的分速度相等，由于v2垂直摆线，摆线平行于斜面，故v1垂直斜面的分速度和v2相等，如图7所示，即
v1sinθ=v2
联立以上各式解得：摆球速度
v2=88205gL
小结 示例可见，掌握了物系关联速度特征，问题也就迎刃而解.
例2 已知一根不能伸长的轻绳，当绕过不产生摩擦的两个轻质小定滑轮O1、O2和质量mB=m小球相互连接，如图8所示，另一端和套在光滑直杆上质量m=mA小物块相连接，如果直杆两端固定，和两定滑轮在同一竖直平面内，那么水平面的夹角θ=60°，两定滑轮和直杆上C点都在相同高度，C点到定滑轮O1的距离为L，重力加速度为g，若直杆是足够长，小球运动过程中不存在与其他物体相碰.现将小物块从C点由静止释放，求：
（1）物块下滑时的最大距离.
（2）物块在下滑距离是L时的速度值.
（3）若小球在下降最低点时候，小物块的机械能（取C点所在的水平面为参考平面）.
解析 （1）设小物块下滑的最大距离为sm，该过程小球升高Δh=L′-L，如图9所示，系统内仅重力和弹力做功，无其它力做功，机械能守恒ΔEA=ΔEB，得：
mAgsmsin60°=mBgΔh
式中mA=mB=m，又依余弦定理可得：
L′=L2+s2m-2Lsmcos60°=L2+s2m-Lsm
或根据勾股定理得：
L′=（Lsin60°）2+（sm-Lcos60°）2=L2+s2m-Lsm
联立解得：sm=4（1+3）L
（2）设小物块下滑距离L时速度为v，此时小球回到初始位置且有向上
的速度vB，如图10所示，由系统机械能守恒ΔEp=ΔEk，得：
mAgLsin60°=12mAv2+12mBv2B.
式中mA=mB=m，又沿绳方向的分速度大小相等，故
vB=vcos60°，
联立解得：v=203gL5.
（3）小物块释放后下滑，滑轮O1左侧细绳先缩短，小球下降；小物块通过滑轮O1左侧细绳垂直杆的位置后，O1左侧细绳开始伸长，小球上升.故小物块到达滑轮O1左侧细绳垂直杆的位置时，小球下降到最低点且速度为零.此时，小物块势能虽可求，但因小球初始位置未知，导致小物块的动能无法求出，故需通过转换，利用过程系统机械能总量不变求解.
设小球初始位置在滑轮O2下方h处，取C点所在的水平面为参考平面，此时系统的机械能为E1=-mBgh； 小球下降到最低点时，设小物块的机械能为EA，小球的机械能为EB=-mBg[h+L（1-sin60°）]，则系统的机械能为
E2=EA+EB=EA-mBg[h+L（1-sin60°）]，
由E1=E2得：
-mBgh=EA-mBg[h+L（1-sin60°）]
解得：EA=mgL（1-32）
- 新闻传播在农村经济发展中的作用探究
- 互联网时代银行客服中心服务转型趋势研讨
- 农产品直播运营的可行路径探讨
- 金融支持苏北农房改善的创新方式研究
- 农村“三变”对农村产权交易的影响研究
- 浅析淮阳县推进农民工返乡创业的实施路径
- 新经济背景下高校家庭经济困难学生心理健康工作探究
- “互联网+”背景下高职市场营销专业人才培养模式探析
- 浅议国土资源规划与可持续发展
- 临县野菜资源现状调查与开发建议
- 探究生态村发展问题及应对方案
- 决胜决战脱贫攻坚战略背景下税收优惠推动 涉农产业发展的政策研究
- 绿色金融对江西省文化产业结构调整的作用效应研究
- 浅析徐州四大战略新兴产业未来发展方向
- 践行核心价值理念 促进农场和谐发展
- 探析礼仪文化在旅游业中的应用发展
- 中小企业跨境电商运营模式分析
- 探究影响建筑工程经济管理的因素及优化措施
- 农村信用社人力资源管理问题分析及改善措施
- 企业管理信息化存在的问题及改进措施分析
- 探析高职电商专业社会服务的实践与思考
- 乡村振兴战略视阈下扶贫模式优化与实现路径
- “一带一路”背景下中印双边贸易潜力研究
- 基于支付意愿理论的激励性食品安全治理研究
- 雄安新区建设背景下保定市智慧物流发展对策研究
- pimple
- pimpled
- pimplelike
- pimples
- pimpliest
- pimpliness
- pimply
- pimps
- pin
- pinafore
- pinafored
- pinafores
- pinball
- pinballed
- pinballs
- pincer
- pincers
- pinch
- pinchable
- pinched
- pincher
- pinches
- pinch-hit
- pinch hit
- pinch-hits
- 娆败
- 娇
- 娇丽
- 娇亮
- 娇人
- 娇俏
- 娇倩
- 娇儿
- 娇儿呆女
- 娇养
- 娇养不如历艰
- 娇养放纵
- 娇冶
- 娇凤
- 娇哥儿
- 娇啼
- 娇啼嫩语
- 娇喉
- 娇喉百转
- 娇喘
- 娇嗔
- 娇嗲
- 娇声
- 娇声娇气
- 娇声嫩语