《基于Geogebra软件的中职数学课堂设计》-工学论文，通信论文-论文范文参考-科学狗论文网

标题

基于Geogebra软件的中职数学课堂设计

范文

高芹

摘? ?要：文章从备课设计、课上设计与测试反馈设计3方面探究Geogebra在中职数学课堂教学设计中的应用，以期将软件在中职数学教学中的作用更好地发挥出来，优化中职数学课堂设计及其教学效果。

关键词：Geogebra软件;中职数学;课堂教学设计

中职数学教学主要是对学生的基本数学能力进行培养，为学生今后的数学发展十分重要，教师需要在教学过程中做好课堂教学的设计工作，把握关键点，提高学生学习效率。但是长期以来，中职数学教学多强调知识的传授与技能的训练，课堂教学大多对灌输式讲授法予以采用，学生的学习通常是听讲、模仿、记忆并再现教师所授知识，属于被动接受知识并强化存储的过程。教学方法上的单一令学生对数学学习产生枯燥乏味之感，越学兴趣越低。针对这种情况，文章试图在中职数学课堂设计中对Geogebra软件加以应用，让更多中职数学教师及学生了解Geogebra的强大功能与易用性的同时，以该软件为支持优化数学课程的教学效果，实现数学教学模式的转变。

1? ? Geogebra软件的特点与功能

1.1? Geogebra特点

Geogebra是一款结合几何、代数与微积分的免费动态数学软件，含直线、向量、曲线以及函数等基本元素在内，可通过便捷化的动态演示对轨迹的生成过程进行探索与显示，将代数、几何图形内在关系的环境展示出来，令抽象而枯燥的数学内容变得具体、生动与形象[1]，特点如下：（1）功能强大，软件集几何作图、数据运算与数据处理等于一体，在中职数学的教与学中十分适用，可省去多个软件相互切换的工作。（2）易于交流与学习，软件内含“作图过程”及“作图过程导航条”工具，能将教案的制作过程再现，做到“所见即所得”。（3）几何属性多样化，软件内置较多的几何体属性，包括圆锥曲线、极线、切线以及函数求导等内容，颜色亦有多样化的呈现。（4）自定义工具属性，在绘图过程中，Geogebra提供制定的输入与输出物件，师生可在工具列上建立所需绘图工具，Geogebra网站的wiki中还提供了丰富的图案与工具以供使用。（5）免费共享，Geogebra以Java程序为基础而编写，可为远程交流及网上学习提供便利[2]。

1.2? Geogebra功能

（1）快速而精确的作图功能。Geogebra可快速、直接地作出很多基本图形，如点、线、向量、多边形、圆、角等，亦能直接在命令列中输入代数表达式，获取相应图形，左边代数区、命令列与绘图区均能进行参数的修改，通过对数值精度的设置，满足精确度要求。（2）实时动态的图形变化功能。Geogebra的工具栏可快速而又动态地实现图形的对称、反演、平移以及缩放等功能，软件左侧代数区会以代数式的形式将图形显示出来，并随着图形的变化而动态改变，同时，动态跟踪对象轨迹。（3）强大的测量与计算功能。Geogebra中的工具欄能对长度、角度、弧长以及封闭图形的周长、面积等进行直接的测量，在左侧代数区显示运算结果。除了可以执行常见的四则运算、指数与对数运算、三角函数运算外，Geogebra的函数运算、科学计算以及统计与微积分功能亦很强大，让师生的运用得心应手。（4）强大的动态函数与方程功能。Geogebra软件可进行函数与方程图像的边界绘制，且将它们的生成过程动态地呈现出来。在绘图区进行图形的绘制之时，Geogebra代数区可动态显示对应图像的代数表达式，若在软件命令栏中输入某一点、向量、函数或方程，代数区与绘图区还会同时显示对应对象。无论对象发生怎样的变化，该对象的全部表达方式均会实现动态的连接与调整，体现出很好的动态效果。

2? ? 应用Geogebra软件设计中职数学课堂教学

狭义层面分析，中职数学课堂教学的设计应包括备课设计、课上设计以及测试反馈设计3大环节。分析其具体内容，备课设计包括撰写与制作教案及课件;课上设计包括探究教学双向互动以及数学实验课等;测试反馈设计则对命制、批改、评讲课堂练习及大中型测试试卷等各类题目予以涉及[3]。

在备课设计环节中，应主要利用Geogebra生成精确的教学图形与图像，将其在教案与课件中应用，这一点在进行平面几何及几何课程的讲解之时尤为重要。教师应在精心构思中将各种动画的演示与渐变效果体现出来，节约课上描点绘图的时间，提高备课效率，获取能够媲美教材的教案及课件。课件库与基本元库的全校共享有利于教师备课及命题效率的提高。

在测试反馈设计环节，Geogebra的作用与备课设计环节大体一致。但有一点需要指出，随着计算机硬件价格的普遍降低与各中职院校机房的普及，利用Geogebra开展数学课堂教学设计与实验并以此为依据对学生的数学成绩进行综合评价可行性已很明显。

课上设计环节是中职数学课堂教学设计的真正实施环节，亦是应用Geogebra的中心环节，应围绕以下两点进行重点设计。

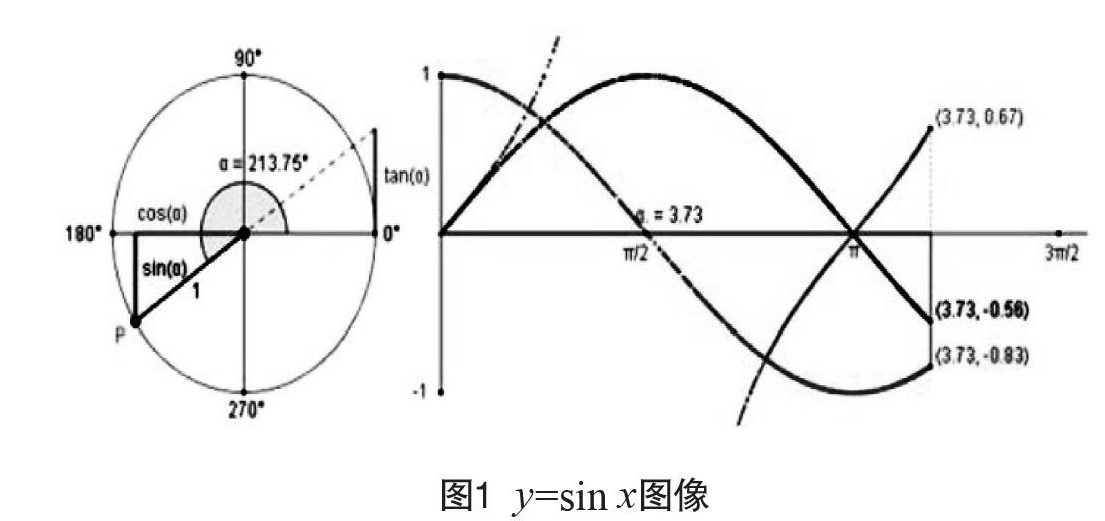
（1）通过对动画演示渐变过程的制作，将诸多教师讲解难、学生理解难的内容动态展示出来。例如，利用单位圆进行y=sin x图像的绘制，如图1所示，通过直接的拖动以及对坐标轴比例的变化，可将y=sin x图像向的渐变过程生动地演示出来。

（2）通过数学实验课（一人一机），开展探究性活动，对学生的动手能力与自主学习能力以及细心、不怕困难的思维品质进行培养。学生是实验课程的真正探索主体，教师在其中发挥组织者、指导者与问题初步提出者的作用。课上设计工作应做到让学生根据教师提出的初步问题进行逐步的分化、细化与求精，借助Geogebra的强大图形及代数功能寻找相应问题的具体解决思路与方案，同时，在探索中提出新问题。

例如，让学生利用平面几何方法对三角形“五心”向量表示的正确性进行验证。

已知采用向量运算的方法输入（A+B+C）/3便可在几何区将ΔABC的重心点直接显示出来。实际上，借助角度的正余弦计算以及向量运算能够给出“五心”的向量表示。于是通过平面几何方法做出三角形的“五心”并与之对比，可以发现两者是重合的，这意味着向量表示具有正确性。此处学生可在Geogebra作图区的任意位置绘制三角形，并对其进行随意的拉动。

下面的公式为在Geogebra命令框内输入以下两命令之后的结果：

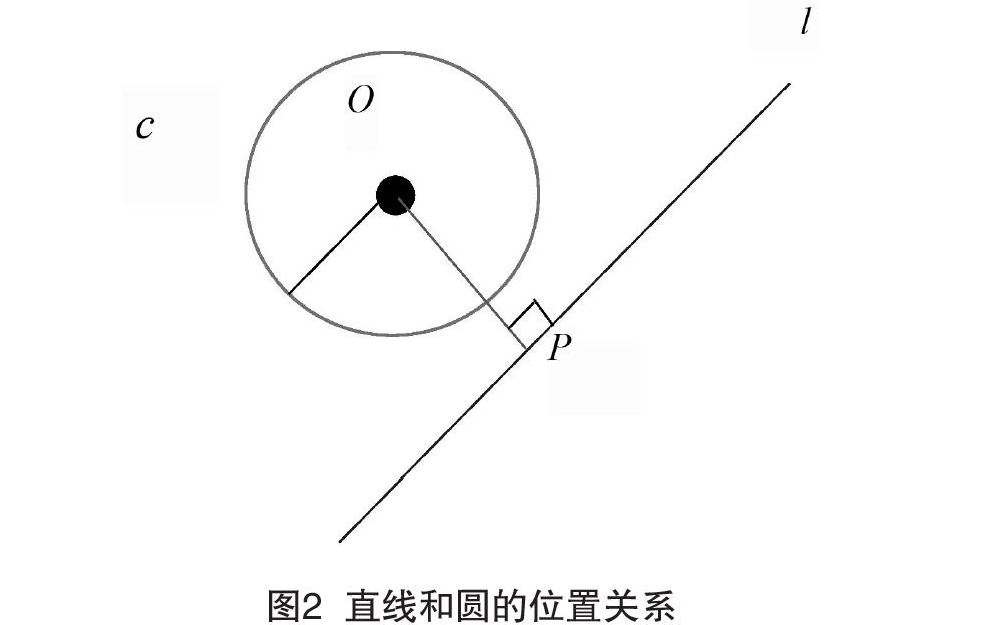
又如，在实验中，通过对圆的半径以及圆心到直线的距离的改变，让学生在最短的时间内进入情景，对r，d对直线及圆位置的影响有一个直观的感受。可通过设计以下问题来完成：已知直线l∶3x-y-6=0与圆心为C的圆x2+y2-2x-4y=0，对直线l与圆的位置关系进行判断，若相交，求取它们交点的坐标。

已知直线与圆的位置关系包括相离、相切与相交3种，各关系交点的个数分别为0个、1个与2个。根据所学知识图像的变化可知，若圆心与直线之间的距离d比圆的半径r大，则两者之间是相离的。若d=r，两者相切;而若d

图2? 直线和圆的位置关系

3? ? 结语

相较于当前流行的几何画板而言，Geogebra软件所具有的功能更强，易用性更加突出，应在中职数学课堂设计及其教学中得到广泛的应用。在Geogebra穿针引线的作用之下，中职数学的课堂教学各个环节可实现有效的整合，它对中职数学课堂设计及教学效果的优化是显著的。

[参考文献]

[1]沈翔.GeoGebra基本操作指南[M].北京：高等教育出版社，2016.

[2]靳菲菲，侯艳.GeoGebra软件对中学数学课堂的影响[J].科协论坛（下半月），2012（1）：180-181.

[3]徐炳林，刘淑艳.GeoGebra在数学教学中的应用[J].中学数学研究（华南师范大学版），2013（13）：23-24.

Abstract：This paper makes a research on the application of Geogebra in secondary mathematics teaching design from prepare lessons， in class and test feedback 3 aspects， hoping that can play the softwares role preferably， and optimize secondary mathematics teaching design result.

Key words：Geogebra software; secondary mathematics; teaching design

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。