《数制之间的转换》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

数制之间的转换

范文

摘要：数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。在数制计算中，一般采用的是进位计数，按照进位的规则进行计数的数制称为进位计数制。在日常教学中我们通常用到不同计数制相互之间的数据转换，不同数制之间的相关转换对中职学生来说学习起来比较困难。本文从教学的角度对不同数制之间的相关转换做了举例说明，便于学生掌握不同数制之间的数据转换。

关键词：数制转换;二进制;八进制;十六进制

中图分类号：TP311文献标识码：A

文章编号：1009-3044（2020）19-0206-03

开放科学（资源服务）标识码（OSID）：

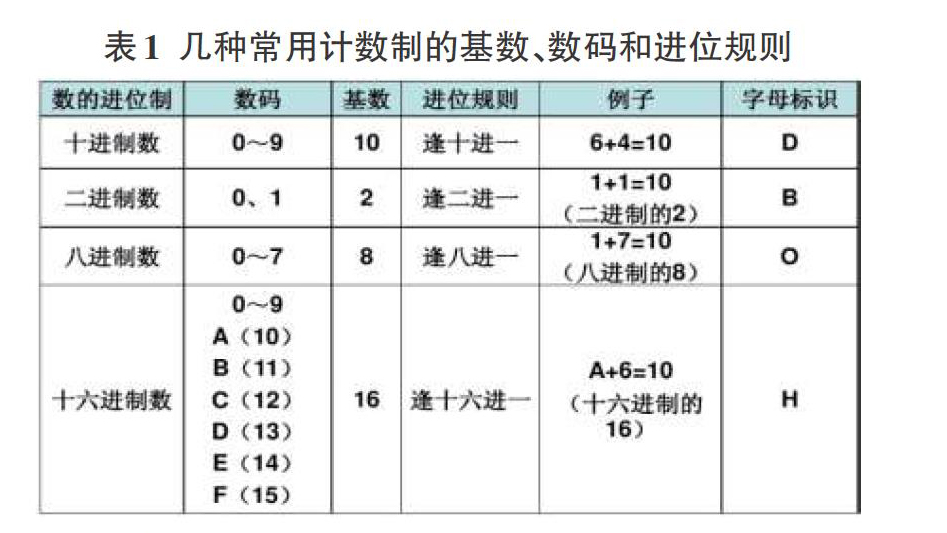
数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。任何一个数制都包含两个基本要素：基数和位权。

我们日常生活中常用的计数方法是十进制，十进制的进位法则是：“逢十进位，向前进一。”像这样按进位的法则进行计数的方法就叫作进位计数制。“进位计数制”简称为“数制”或“进制”。由此我们可以推断出，每一种数制的进位都遵循一个规则，那就是逢N进一。这里的N叫作基数。所谓“基数”，就是数制中表示数值所需要的数字字符的总数，比如，十进制中用0、1、2、3...9来表示数值，一共有10个不同的字符。二进制中用0、1来表示数值，一共2个字符。十六进制中0-9、A、B、C、D、E、F，一共有16个不同的字符。为了区别不同的进制数，常在不同进制数字后加一字母表示：十进制D（Decimal）、二进制B（Binary）、八进制O（Octal）十六进制H（ Hexadecimal）。

我们来看下面的例子：

问题：十进制数9999.999，这其中的7个9代表的含义一样吗，有什么不同？

从左向右，第-9表示9000，第二个9表示900，第三个9表示90，第四个9表示9;小数点之后的第一个9表示0.9，第二个9表示0.09，第三9表示0.009。

9999.999=9x1000+9x100+9x10+9+9x0.1+9x0.01+9x0.001

1000=103. 100=102， 10=10l， 1=100， 0.1=10-10.01=10-2

0.001=10-3。这就叫位权，也就是基数的若干次幂。例如，我们可以把9999.999表示成：

9999.9999=9X103+9X102+9X101+9x100+9x10-1+9X10-2+9X10-3

这种表示法就叫按权相加法。也就是让每一位上的数字字符乘以它所代表的权。

1 数制的转换

计算机在进行数据处理时首先把输入的十进制数转成计算机所能接受的二进制数;计算机运行结束后，再把二进制数转换成人们所习惯的十进制数输出。这种将数由一种数制转换成另一种数制称为数制间的转换。

十进制数转二、八、十六进制数的方法如下表：

1.1十进制数与二进制数之间的相互转换。

例如：把十进制数35.625转换成二进制数？

【1）十进制整数转二进制整数数

十进制整数转二进制整数采用“除2取余，逆序排列”法。

具体做法：用2去除十进制整数，可以得到一个商和余数;再用2去除商，又会得到一个商和余数，如此进行，直到商为零时止，然后把所有余数按逆序依次排列。

（2）十进制小数转二进制小数。

十进制小数数转二进制小数采用“乘2取整，顺序排列”法。

具体的做法：用2乘以十进制小数，可以得到积，将积的整数部分取出，再用2乘以余下的小数部分，又会得到一个积，再将积的整数部分取出，如此进行，直到积中小数部分为零，或者达到所要求的精度为止，然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为二进制数的低位有效位。

35.625D=（IOOOII.IOI）B

（3）_进制数转十进制数。

二进制数转十进制数采用“按权相加法”。

例3：1IOI.10IB=（）D

1101.101B=1x23+1x22+0x21+1x20+1x2-1+0x2-2+1x2-3

=8+4+0+1+0.5+0+0.125

=13.625D

1101.10IB=（13.625）D

1.2十进制整数与八进制数之间的转换。

八进制数的一共有0、1、2、3、4、5、6、7八个字符。同理，我们可以采取“除8取余，逆序排列”法，将十进制整数转换成八进制整数。

同理：对于要转换的十进制数的小数部分，则应不断地乘以8，并记下其整数部分，直到结果的小数部分为零或达到需要的精度为止。

例5：0.635D=（0.5050）0

0.635x8=5.08 -5

0.08x8=0.64 -0

0.64x8=5.12 -5

0.12x8=0.96 ……O（后續省略）

例6：（2157）0=（）D

（ 2157） 0=2x83+ 1x82+5x81+7x80=1024+64+40+7=1135D

1.3十进制数转与十六进制数之间的相互转换。

十六进制中0-9、A、B、C、D、E、F，一共有16个不同的字符，其中A、B、C、D、E、F分别代表十进制的10、11、12、13、14、15。同理，我们也可以采取“除16取余，逆序排列”法，将十进制整数转换成十六进制整数。

例8：（46F.1）H=（）D

46FH= 4x162+6x161+Fx160+lx16-1

=4x256+6x16+15x1+0.0625

=1024+96+15+0.0625

=1135.0625D

同理：对于要转换的十进制数的小数部分，则应不断地乘以16，并记下其整数部分，直到结果的小数部分为零或达到需要的精度为止。

1.4二进制数与八进制数之间的相互转换

方法：以小数点为界，向左右每3位一组，在高位和低位不足3为时用0补齐。

例9：1110101.111B=（）0

二进制：001

110 101. 111

八进制：1 6 5.

1110101.10IB=（165.7）0

例10：（144）O=（）B

（ 144）0=（001100 100）B

4 4

1.5二进制数与十六进制数之间的相互转换

方法：以小数点为界，向左右每4位一组，在高位和低位不足4位时用0补齐。

例11： 110110lOI.111B=（）H

二进制：0001 1011

0101. 1110

十六进制：1 8

5. E

110101.101B=（ IB5.E ）H

例12：AF2BH=（）B

AF2BH=（ 1010 1111 0002 1011）B

2 B

2 结束语

十进制转N进制，整数部分采用“除N取余，逆序排列。”法，小数部分采用“乘N取整，顺序排列”。数制之间的相关转换，重点和难点是掌握十进制与二进制、八进制、十六进制之间的相互转，不同数制之间的相互转换是计算机专业的学生必须掌握的基础知识。

除了掌握以上的數制转换方法，还可以尝试学习另外的一种数制转换方法“降幂法”。

【通联编辑：梁书】

作者简介：杜双敏（1981-），女，河南鄢陵人，讲师。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。