网站首页  词典首页

请输入您要查询的论文：

　

标题 基于层次分析法的输变电工程综合效益后评价
范文 刁海璨+袁圆+朱壮明
摘要：目前，我国对于工程投资的经济效益研究比较充分，但对于投资项目的社会效益评价尚未形成完整体系，缺乏社会效益的定量测算，在具体项目评价中的应用相对缺乏，且存在一定的不均衡性。输变电重大工程投资大、影响范围广的特点决定了工程投资综合效益中需更多关注社会效益，需充分考虑其社会效益与经济效益的协同性，以确保项目与其所处的社会环境协调发展。本文选取了一个典型的输变电工程，采取层次分析法进行测算，验证了该方法在输变电工程综合效益后评价方面的有效性和可操作性。
关键词：输变电重大工程 综合效益评价 协同优化 层次分析法
中图分类号：TM72 文献标识码：A
“十三五”期间，我国将建成特/超高压交直流混合输电网，并推动全球能源互联，公司围绕“建设能源互联网，推动我国能源利用方式变革”的总体目标，将迎来公司发展方式和电网发展方式转变的重要机遇期。
在这种电力建设背后的发展观念产生重大转变的背景下，结合其他输变电重大工程项目的效益后评价进行实证分析，建立一整套输变电重大工程经济效益和社会效益评价体系，对输变电重大工程项目的经济效益和社会效益进行综合评价，以定量的方式进行重大工程投资决策，以及通过对模型的敏感性分析等手段对项目建设的规模、标准、时机进行优化，有利于提高输变电重大工程项目的决策水平，有利于全面提升项目的经济效益和社会效益，有利于后续输变电重大工程的决策和管理，对全面实现两个一百年战略目标，共圆中华民族伟大复兴中国梦具有十分重大的意义。
1 层次分析法原理
层次分析法是将决策问题分为目标、准则、方案三个大的层次，以决策者对每两个指标之间相对重要性的主观判断为基础，以判断矩阵的特征向量为依据，得出下一层次的各个元素对上一层次特定元素的优先权重，再递归得出方案层中的备选方案对总目标的最终权重，在加权评价体系下得分最高或最低者（取决于实际问题）即为最优方案。此处的“优先权重”是相对值，表明各方案对某一子目标以及各子目标对上一层目标的相对重要程度。这种方法比较适合那些评级指标分层交错，而最终目标又不便于定量描述的决策模型。
AHP方法解决实际问题的大致步骤如下：
1.1建立递阶层次结构模型
应用AHP分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。这些层次可以分为三类：最高层（目的层），中间层（准则层），最底层（方案层）递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地层次数不受限制.每一层次中各元素所支配的元素一般不要超过9个。
1.2构造出各层次中的所有判断矩阵
准则层中的各准则在目标衡量中所占的比重并不一定相同，在决策者的心目中，它们各占有一定的比例。引用数字1-9及其倒数作为标度来定义判断矩阵A=（aij）n×n。标度越大表示两个因素相比，前者比后者更重要。
1.3层次单排序及一致性检验
1.3.1计算一致性指标CI （consistency index）
2 层次分析法在输变电工程综合效益评价中的应用
电网工程的建设和运维阶段，除直接经济效益外，会产生大量的社会效益，主要包括：狭义社会效益、环境效益、间接经济效益。其中，环境负效益的减少可以带来更大的狭义社会效益，同时间接经济效益的增加一定程度上会增加环境负效益，三者相互依存，相互影响。直接经济效益和社会效益任何一个目标的变化必然引起另一个目标的变化，从而影响整个工程的社会综合效益。如何在满足各项环境、系统指标要求的前提下，通过直接经济效益和社会效益的协同优化，实现社会综合效益最大化是模型构建的主要目标。
宁东直流工程是世界首个正负660kV级的直流输电工程。这项工程起自“塞上江南”的宁夏首府银川（“宁”），终到黄海之滨的山东第一大城市青岛（“东”），全长1335千米，经宁、陕、晋、冀、鲁共计五省43县之地，是“西电东送”战略的重要成果，故选择此项目进行研究。
根据问题描述的基本需求，结合主要变量及参数，且同时设定经济系统动态平衡约束、增长约束、经济效益与社会效益之间的制约等约束条件。根据神经网络与模糊综合评价方法对于输变电重大工程的评价指标进行梳理，设计了三层指标体系。一级指标层为综合效益，二级指标为社会效益和经济效益，而三级指标分别为社会效益指标下的22个指标和经济效益指标下的9个指标。在完善的指标体系基础之上，构建量化的经济效益和社会效益最大化双目标优化模型如下。
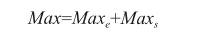
2.1计算特征根和特征向量
权重计算采用本征向量法，即： 先求出各优先矩阵的最大特征λmax ，然后，分别计算与各λma x相对应的本征向量B，各本征向量B中的各分Wij即为各指标的相应权重，其计算结果如下：第二层有一个优先矩阵，其最大特征值λmax= 2，对应特征向量B为：B=[0.2680 0.7320]
第三层的优先矩阵，其最大特征值λmax= 82，对应特征向量C为：
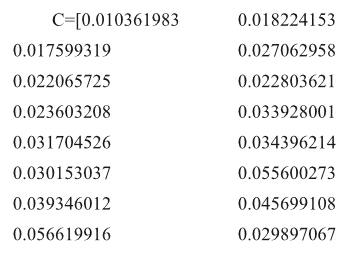
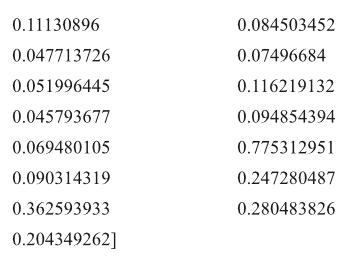
最后計算综合权重。第三层各指标的综合权重W3i为第三层各指标权重W3i与它们所属的上层指标的权重之积； 举例说明如第三层“户均电器拥有量增长贡献”指标综合权重W3i= W3i× W2i=0.010361983×0.2680=0.002 777011。

由此，我们可以得出如下表所示的31项指标的权重矩阵如下：
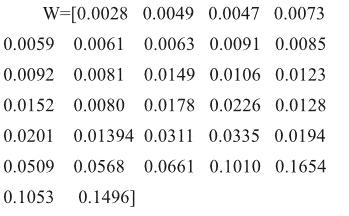
2.2模型求解
根据建立的输变电工程综合效益最大化模型，将求得的权重代入得：
Max=-3.20555013091328×10-7×Q2+14.2378042425847×Q+1484365225.38 43
解得当Q=22208051.132时，函数有最大值1642462167.69766。
也即该工程社會综合效益最大化前提下的输电量为22208051.132kWh，当年的社会综合效益理想值为1642462167.69766元。
3 结果分析
根据层次分析法求得的结果，经济指标的权重高于社会效益指标，在此情况下得出了与该工程设计的最大输电量相近的最优解。这样的设定考虑了当前我国仍以经济发展为第一要务的国情。但是即便不考虑受主观因素影响的权值，将各指标数值简单相加，得出结果仍然在千万千瓦时的数量级，并不影响本文的结论。
4 结论与建议
本文采用理论与实际相结合的方法，在研究分析输变电工程经济社会效益的基础上，制订具体的经济效益与社会效益协同优化模型，对中大输变电项目可能带来的经济效益与社会效益的权重进行了分析讨论。通过层次分析法确定协同优化模型中二者及其下级指标的比重，使得在此基础上构建的输变电重大工程经济效益与社会效益协同优化模型更加准确和科学。
本文建立的评价指标是基于大量收集社会效益评价领域的研究成果加以模糊社会网络分析方法，并结合电网工程自身特点综合得到的，考虑到现有社会效益评价尤其是针对电网工程的相关研究与实践尚不完善，还不具备开展大量统计研究的条件，使得指标体系存在一定的局限性。今后可对本课题所提出的指标体系的合理性和完整性进行进一步检验和完善，并对研究提出的评价模型进行修正。
参考文献：
[1] 朴春花.层次分析的研究与应用[D].华北电力大学，2008.
[2] 陈宝谦，李淑冰等.正互反阵的一个特征值问题[J].高校应用数学学报，1991，6（1）：57- 65.
[3] 王雪华，秦学志等.AHP中判断矩阵一致性修正的模式识别法[J].系统工程理论与实践，1997（11）：56- 59.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/10 23:35:54