《数学解题对应说》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

数学解题对应说

范文

王宁珍

如果把数学的解题过程作为一个独立的对象来研究，其本质是寻找一类对应。在很多的解题方法中，大部分同学只用到一种对应关系解题。在小学数学中，解决问题实际大部分有对应规律，只要应用这一规律，解题就会变得简单，具体的解法从宏观上讲，有两种类型。

第一，是从已知条件中找到对应的数量关系式。

这个方法是较常用的一种。有一部分应用题，根据已知条件的结构特征，内容大部分是围绕对数量关系式的应用来展开的，例如：功效×时间=工作总量、速度×时间=路程、单价×数量=总价，倍数、和倍、差倍问题，周长、面积、体积计算问题，植树问题等，这类题都有数量关系式和公式，在已知条件上具有一定的对应关系，什么结构的式子用什么样的表达式，这是我们常用的一种解题方法，相对来说比较简单。

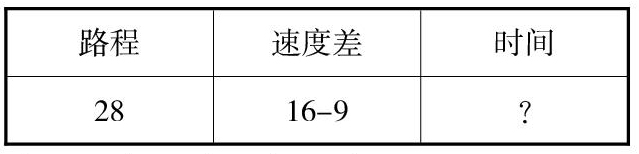
例如：甲在乙后面28千米处，两人同时同向而行，甲每小时行16千米，乙每小时行9千米，甲几小时追上乙？

分析：甲每小时比乙多行16-9千米，也就是甲每小时可以追近乙（16-9）千米，这是速度差。已知甲在乙后面28千米（追击路程），28千米里包含着几个（16-9）千米，也就是追击所需要的时间，根据数量关系：路程=速度×时间可列对应关系表：

由此算出：28÷（16-9）=4（小时）

第二，是从文字中找到对应的数学表达式。

这是我们要钻研和研究的对应关系，即找到一个从文字到数学表达式的等价对应，或者说是一一对应，也就是常说的数学化。简单的一种：列方程解应用题，首先是未知量与字母x对应（设未知数，我们常用x、y等字母），然后是其他相关量与含x的代数式对应（表达相关量，这一过程很重要），最后是这些代数式与题目中的等量关系对应（产生方程）。数学的学习过程相当于寻求这些对应。

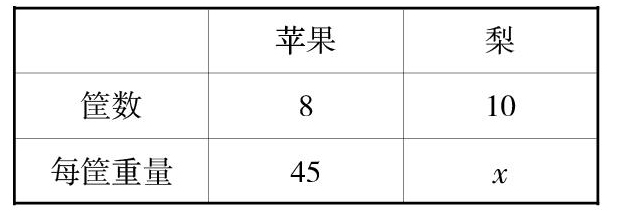
例如商店运来8筐苹果和10筐梨，一共重820千克。每筐苹果重45千克，每筐梨重多少千克？

对应关系：

解：设每筐梨重x千克

45×8+10x=820

从这个角度来说，数学解题是一个翻译过程，因此说数学是一门语言。当学生用对应法解题熟练后，就会体会到这样一个程序化的过程，数学的任务是寻找各类公式、定理，尽可能地用这些来表达整个世界！从这方面理解数学知识的产生、形成与发展的过程，既简单又是对数学内容更深层次的理解。当然有些题要找到对应关系就需要把已知条件进行等价变形，转换思维，才能成为对应关系。例如：

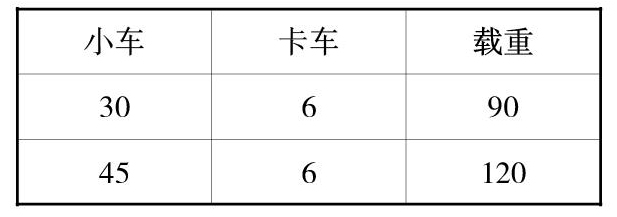
1.30辆小车和6辆卡车一次运货90吨，45辆小车和6辆卡出一次运货120吨。每辆卡车和每辆小车每次各运货多少吨？

对应关系：

比较条件，看看什么量变了，什么量没变，两个变化的量之间的關系是什么？从对应量的变化，可以看出（120-90）吨正好与（45-30）辆小车的载重量相对应，因此每辆小车每次可以运货（120-90）÷（45-30）=2（吨），那么每辆卡车每次可以运货（90-2×30）÷6=5（吨）

2.同学们采集植物标本，六年级采集了120件，比五年级的3倍少36件。五年级采集了多少件？

对应关系：

五年级采集的标本数看作1倍量，那么3倍量所对应的是（120+36）件，所以五年级采集的标本数是（120+36）÷3=52（件）。

这样就可以大大减小解题难度。著名数学解题大师唐以荣曾在他的著作中提到“数字解题其实质就是变形的艺术”。只有找到对应关系，才能体现出智力活动源泉这一基本思想。

小学解决问题中，有一半以上数学题都能寻找到一种对应，或者称之为信息加工，所谓信息加工就是对题目表象的文字、数据、情景图片等做诸如组合、分离、焦点关注等深层次的思维加工，从而产生认知上的相同或相似，但这些相同或相似不一定是数学的。原有的知识基础和生活经验，都可以找到不同的对应关系。但有些题可能导致不同认知。这些不同的认知，有些对数学有用，具有正迁移的作用，可以诱发学生创新认识，拓展空间;有些对数学解题无益，尤其是那些错误的认知。从无知中走出来是相对较容易的事，但摆脱误知是相当困难的。要找到一条绕过障碍的出路，能让学生正确解决问题，用对应关系解题是培养学生解题能力的主要途径。但同一个问题，可能不同的人从不同的方向理解成不同类型的问题，这样就产生了一题多解，也就出现了数学解题的多样性，这恰恰是数学追求的境界。但大部分学生做到这一点较困难。

总的来说，用对应法解决问题是一个高度抽象的问题转化成简单的概括。要找到解题对应关系，使学生成为有效的问题解决者，是对教师的挑战。教师在教学中就要运用这一方法作为切入点，探究对应关系，寻找规律，发现规律，运用规律，培养学生逐步从中领悟这一规律和解决问题的能力，是数学知识进行潜移默化的另一种牵引，增加了解决问题的解题精髓，努力帮助学生不断实现自我超越——赢自己，学有道。

参考文献：

[1]中国教师智库数学配人教版四年级下《鼎尖教案》[M].延边教育出版社，2017-12.

[2]《课程标准教案》数学五年级下适用人教版[M].上海交通大学出版社，2017-3.

编辑郭小琴

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。