《巧借反例活化高中数学教学》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

巧借反例活化高中数学教学

范文

薛海琪

【摘要】高中阶段的数学知识难度极大，并且需要证明的内容较多，数学知识的逻辑性强，理论性强，而且部分知识在正向证明时所需的步骤烦琐，计算量大，学生常常在听讲后仍然处于迷茫状态，无法准确把握要学习的内容，增加了学习的难度.此时就可以通过反例来反向证明，许多知识点在反向证明时反而计算量减小，能降低学生理解的难度.巧借反例能够让学生更好地掌握数学知识，提高学生运用知识解决问题的能力.

【关键词】反例;高中;数学教学

引言

借助反例证明，就是指教师在教学时要证明一个命题是假命题，可以举出具备命题成立的条件但是不具备命题结论的例子.通过反例进行教学能够使一些正向论证极为困难的问题在短时间内被解决，当学生了解到反例能够成立时自然也就意识到例子是错误命题.这种反例的说服力反而更强，能够有效培养学生的逆向思维能力，活跃学生的思维，让学生体验数学的奥妙，降低高中生学习数学的心理负担.基于此，本文将从反例在高中数学教学中的应用方法入手展开探讨.

一、借助反例引导学生理解数学定理及公式

高中数学中的定理和公式一般采用的是准确精练的形式，一个大概念往往就用最准确的几个数学符号或者汉字作为定理的解释，这样看起来的确比较便利，但是学生在理解起来却较为困难，尤其是多个知识点相结合的教学内容，更是增加了学生理解的难度，很容易使学生产生混淆感，从而使学生在学习时遇到重重困难，影响课程教学质量.[1]

以《曲线和方程》的教学为例，

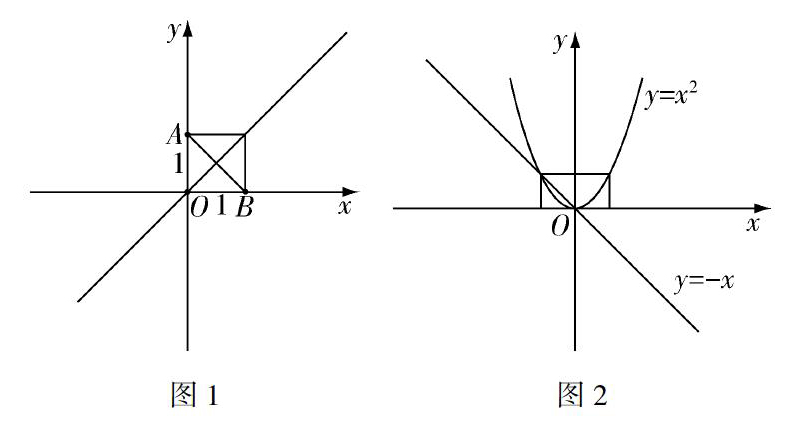
这一单元的概念较抽象，且需要学生思考的内容多，对于高中生来说理解难度不小.为了让学生能够更好地掌握此节课的内容，教师可以先利用原先学过的知识来引入新的知识，可以先提出问题：（1）求图1中AB的垂直平分线的方程;（2）画出方程x+y=0所表示的直线和方程y=x2所表示的曲线.可以得出图1的直线方程是y=x，第二问的直线、曲线如图2.

在此基础上教师可以提出新的问题：方程f（x，y）的解与曲线的坐标应该具备怎样的关系才叫方程的曲线或曲线的方程？学生能够总结出“曲线上的点的坐标都是方程的解”和“以方程的解为坐标的点都在曲线上”后，教师不要急于直接给出曲线方程的定义.为了加深学生的印象，教师可以采用反例法进行教学，如举出三个比较具有代表性的反例公式，分别是 x-y=0，x2-y2=0，|x|-y=0，然后给出如图3所示的直线c，询问学生以上方程可以表示直线c吗，待学生得到不能的结论后，教师就可以与学生一起分析这三个方程式，最后带领学生根据这三个方程得出曲线的方程、方程的曲线的具体概念.

二、利用反例帮助学生复习以前学习的知识

数学知识的内在联系性很强，同时由于高中数学难度较大，这也使得教师很少有时间带领学生复习前面的知识，但是教师可以利用反例来帮助学生巩固以前学习的知识，这样做比正向带领学生复习一遍速度要快得多.[2]例如，教师先给出方程4x+a×2x+4=0有解，求a的取值范围.既然是已经学过的知识，那么学生必然能够想到先去设一个未知数m来帮助解题，令m=2x ，然后方程就变成了 m2+am+4=0.一般情况下学生都能够做到这一步，但是再往后对于m的取值范围会有部分学生混淆，此时教师可以提出问题：m<0是否正确？这样学生就会主动回忆概念，翻笔记，翻书，然后他们发现教师刚才给出的结论是错误的，m肯定大于0，而且不会等于0，到这里甚至会有发散思维：底数小于1时会怎样？小于0时会怎样？这样他们对指数函数的概念就印象深刻了.

三、根据反例培养学生思维的发散性及灵活性

通过反例进行教学是培养学生逆向思维的有效途径.高中生要学习的知识十分多，且高中数学知识的联系性较为紧密，如果学生的思维能够具备发散性及灵活性，那么能够促使学生学会灵活运用知识.

例如，在讲解完指数函数 y=ax、对数函数y=logax 和幂函数y=xa后，学生会对这三个函数之间的联系以及约束条件产生混淆，常会出现错用的情况，教师在教学时就可以采用反例法帮助学生更好地理解概念，区分这三个函数之间的约束条件.首先，教师可以提出问题“假如a<0，这三个函数会产生什么样的结果”，让学生进行验证，然后举例x<0，让学生将之代入函数，得出结论，并讓学生观察结论，通过这种方式学生就可以把这三个函数的图像和约束条件分开了.又如，在学完正余弦函数的和差公式后也有很多学生分不清，我们也可以采用类似的方法，这里比较简单的方法是直接举一个特例——直角、平角或0°.这样的方法能够引导学生更好地记忆公式，也利于实际应用.

四、巧借反例，扎实基础

若想提高数学学习水平，那么一定要具备扎实的数学基础，这是学好数学的根本所在，也是高中数学教师开展教学工作的一项最为基本的内容，而学生解题水平的高与低也会受到基础知识夯实程度的影响.由此可见，数学学习基础对于高中生的数学学习来说是至关重要的.但以实际教学情况来看，由于许多学生在初中阶段的数学学习基础就不够扎实，所以在高中阶段学习数学知识时会因此而遇到一些问题，致使高中生的数学学习基础缺乏扎实性.针对上述问题，在现阶段高中数学教学中，教师应做到巧借反例来扎实学生的数学学习基础，使整个高中数学教学能够获得活化，彰显出新的生机与活力.具体来说，一方面教师应把控好数学基础知识所具备的教育价值，另一方面应以探析与尝试的方式，借助反例来实施科学性的变通，以便深化学生思维的拓展教学，防范大量的认知错误以及记忆混淆等方面的问题侵蚀到高中生的思维，促使学生能够正确认知与理解数学知识，真正做到扎实学生的数学学习基础，促进学生对于数学知识的有效性学习.这样做不但能够提高学生的数学学习水平及数学学习成绩，也能够明显提高数学课堂的教学质量与效率，达到新课改之后对于高中数学教学的重要要求.

五、巧借反例，发现问题

以往在开展高中数学教学工作时，教师普遍习惯于采用直接讲述的方式来促进学生理解数学知识，也会在课堂中向学生提出相关的问题，这种问题往往是教师根据高中数学教材中的内容来确定的，未能对问题进行精心的设计，而学生解答问题的欲望则通常较差，且在此过程中也未能积极引导学生去主动发现问题、思考问题以及解决问题，进而致使学生发现问题的能力及解决实际问题的能力均有所不足.然而，一旦产生这种情况，则会致使学生在高中数学课堂的学习中仅仅能够获得较为浅显的进步，难以获得深层次的进步.所以，针对上述情况，在当前的高中数学教学中，教师还应巧借反例来引导学生主动去发现问题.

由于高中数学知识本身就具备一定的抽象性以及复杂性，而高中生的理解能力及学习水平等方面又有着明显的差异性，所以会致使某些学生在学习、理解数学知识的过程中遇到相关的问题，这不但会影响到学生的数学学习兴趣，也会严重消耗学生的数学学习信心.若能够应用反例教学方法，则能够使教师发现高中生在学习阶段存在的问题，并指导与引导学生主动去发现问题，借助良好的方式去解决问题，这样利于深化学生对于数学知识的理解，而且能够提升学生对于自身的正确认知，从而使学生在高中数学课堂的学习中获得诸多层面的进步.

六、巧借反例，高效解题

以往在解题时，许多学生都会直接提出解题思路，导致某些习题的解题方向存在偏差，最终会直接影响到学生的解题质量以及数学成绩.针对上述情况，对于高中数学教师而言，应做到巧借反例，促进学生进行高效性、正确性的解题，尽可能防范学生在解题期间产生偏差性的问题.巧借反例，则能够以反例作为重要的载体，指导学生参与辨识性的数学习题训练，而在此过程中则能够让学生了解到数学问题的另外一个层面，这样做不但能够提高学生的辨别与辨识能力，而且能够强化学生的解题能力，使学生能够在较短的时间内对数学问题进行正确解答，节约学生的解题时间，提高学生的解题效率，进而势必能够提高学生的数学学习成绩，同时能够提高学生的数学学习水平，最终使高中生能够在数学课堂的学习中获得十分深远的进步.因此，在高中数学教学中，巧借反例是尤为关键与必要的，教师应对此予以關注和重视.

结语

综上所述，将反例运用在高中数学教学之中能够提高课堂教学效果与质量，教师在教学时要懂得变通，结合教学内容适当地选择反例进行教学.教师可以借助反例引导学生更加深入地理解数学定理及公式，帮助学生复习以前学习过的知识，加深学生对知识的印象，激发学生的学习兴趣.同时，教师应该借助反例培养学生思维的发散性及灵活性，让学生的思维活跃起来，从而使课堂教学质量得到提高.

【参考文献】

[1]张鹏.巧借反例活化高中数学教学[J].中学数学，2020（09）：74-75.

[2]孙庆括.高中数学中反例的教学功能与构造方法[J].高中数学教与学，2017（12）：34-36.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。