《利用最小二乘与最优控制的水轮机模型参数辨识》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

利用最小二乘与最优控制的水轮机模型参数辨识

范文

侯睿曾云王伟李敏古志吴一凡

摘要：为了改善一般常用水轮机模型基于实测数据参数进行辨识过程中底层编程繁琐的缺点，基于电力系统仿真中常用的理想水轮机数学模型，取134组模拟实测输入输出数据，用最小二乘与基于数值最优化技术的最优控制方法分别进行辨识从而获取参数，并利用两种方法对同一实测数据辨识结果进行仿真对比。算例仿真结果表明，在给定阶跃扰动下，利用最小二乘与最优控制方法进行参数辨识后的模型输出响应与实测响应结果（基于模拟样本数据）误差均低于0.04，且基于数值最优化技术的最优控制辨识效果与实测数据拟合程度更精确，验证了基于数值最优化技术的最优控制方法在线性水轮机模型参数辨识上应用的可行性，为水轮机模型参数辨识方法提供了一种可提升辨识效率的人机对话参考。

关键词：最小二乘算法;线性水轮机模型;MATLAB;最优控制方法;参数辨识

DOI：10. 11907/rjdk. 201173

中圖分类号：TP301文献标识码：A 文章编号：1672-7800（2020）010-0088-06

Abstract：In order to improve the disadvantages of the low level programming in the process of parameter identification based on the measured data of common hydraulic turbine models，based on the ideal hydraulic turbine mathematical model commonly used in power system simulation， 134 groups of input and output data of simulation measurement are used to identify the parameters with the least square method and the optimal control method based on numerical optimization technology， and the two methods are used to compare the simulation results of the same measured data after identification. The simulation results show that under the given step disturbance， the error between the model output response and the measured response （based on the simulated sample data） after the parameter identification of the least square and the optimal control method is less than 0.04， and the identification effect of the optimal control based on the numerical optimization technology and the measured data fit more accurately. The feasibility of the application of the optimal control method based on the numerical optimization technology in the parameter identification of the linear hydraulic turbine model is verified， which provides a man-machine conversation reference to improve the identification efficiency for the parameter identification method of the hydraulic turbine model.

Key Words：least-square algorithm;linear hydraulic turbine model;MATLAB;method of optimal controlling;parameter identification

0 引言

水力发电在我国国民发电总量中的占比越来越重，水轮机作为水力发电主要设备之一，相关研究一直备受关注。由于难以在水电站进行现场实验，进行普通真机实验可能性较低，故通过水轮机模型仿真试验成为主要研究方式之一，建立水轮机这一被控对象的精确化模型成为研究热点。尽管现有水轮机模型研究已相当成熟，且对水轮机模型参数选择已有详尽归纳[1-2]，但由于水轮机模型参数一般是理想化计算，所以尽管水轮机模型可满足普通仿真实验，却并不能较好地贴切水电站实测响应，因此用理想化计算参数模型进行电力系统等仿真实验难以避免较大误差[3-4]。故本文提供一种不同于解析建模而根据现场实测数据（基于模拟样本数据）辨识水轮机模型参数的方法。将水轮机及其调节系统统一进行辨识一并得到优化的控制参数，根据实测数据，对水轮机及引水系统分环节辨识、精细化建模成为水轮机及其调节系统自适应优化控制的数学模型基石[5-6]。通常系统辨识有4种主要目的：①估计具有特定物理意义、可表征系统行为的重要参数;②建立可模仿真实系统行为的模型，使仿真能够反映真实的系统特性;③以目前可测输入输出预测未来演变;④辨识得到描述系统动态特性的数学模型以利于控制器设计[7]。其中对于水轮机，其水力动态特性主要表现在引水系统动态特性中，具有明确物理意义的水流惯性时间常数是恶化机组调节品质的关键因素，但通常未对该参数进行实测，一般通过理论近似计算得到，有一定误差。辨识得到符合真实系统且较小水流惯性的时间常数模型，对于改善调节品质具有一定意义[8]。基于粒子群、引力搜索、差分进化等具有强大的非线性寻优能力的智能算法在模型参数辨识中可发挥良好作用，因此将参数辨识问题转化为参数优化问题已成为趋势[9]。

研究表明，对于线性系统参数辨识采用应用广泛且非常成熟的最小二乘法亦可得到良好的辨识结果。随着MATLAB这一强大的数值仿真计算机工具的出现，对于复杂程度不高的参数辨识问题不必基于底层算法编程才可得以实现，有效利用MATLAB及其Simulink工具，设计人机交互界面，也可在参数辨识等工作中获得良好的辨识结果，并形成具有一定普适性的人机交互辨识对话框[10-15]。文献[13]基于OCD程序对被控对象控制作了大量研究，但应用于水轮机模型参数辨识的研究较少;文献[16]将最小二乘法应用于转向系统的参数辨识，取得了良好效果;文献[17-21]成功地将最小二乘法应用于水轮机模型传递系数求取及曲面拟合等。

综上所述，本文基于最小二乘法成熟且操作简单的优秀特性，对水轮机线性系统参数进行辨识，进一步参考控制领域专家薛定宇教授[13]总结并提出的基于跟踪误差指标的最优控制器设计程序（optimal controller designer），对其Simulink模块环节进行改进以适应于模型参数辨识工作，发现对于根据实测输入输出数据进行模型参数辨识亦可以得到良好的效果，与最小二乘法参数辨识仿真结果比较，验证其与实测数据拟合度。

1 水轮机模型及参数辨识

1.1 水轮机模型

1992年，IEEE Working Group提出了一种广泛应用于电力系统分析的简化的线性化模型。

非理想水轮机流量和出力可表示为：

其中，[Δpt]是水轮机功率增量相对值，[Δq]是水轮机流量增量相对值，[Δy]是主接力器增量相对值，系数aij是传递系数。

在机组并网运行条件下，速度偏差很小，尤其是机组并入大电网运行时。因此，可以忽略Δx的影响。则有：

该理想水轮机模型具有实际物理意义的参数较少，用于参数辨识的实例研究可使问题简化。

1.2 参数辨识

辨识的目的是将实验得到的输入输出数据，根据目标函数，从纷复繁杂的数学模型中确定出数学模型结构。随着模型的参数化，只有当参数均被估计出来，模型才最终被建立，该问题为参数估计。为简化辨识问题，在单输入单输出系统（SISO系统）中根据输入输出的数据序列和已知的模型结构，结合估计理论，选择较优、较简明的最小二乘算法，然后进行参数估计运算。

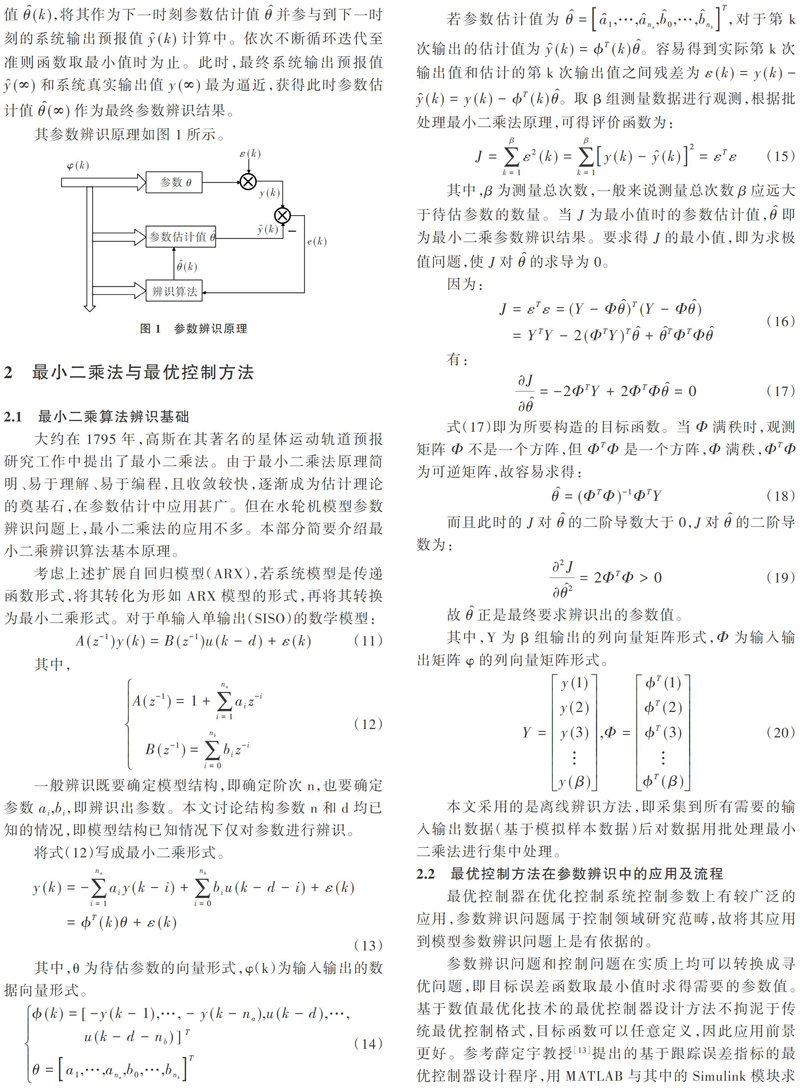
为了获得对象参数[θ]的估计值[θ]，一般采用逐步逼近的方法。[y（k）]为系统实际输出值，[u（k）]为系统实际输入值。在[k]时刻，为得到此时系统输出预报值[y（k）]，需根据[k]的前一时刻参数估计值[θ（k-1）]及当前时刻系统输入输出矩阵值[?（k）]。其计算公式为：[y（k）=?T（k）θ（k-1）]。此时预报误差为[e（k）=y（k）-y（k）]。将预报误差[e（k）]引入辨识的算法中，并且根据某准则条件得出此时参数估计值[θ（k）]，将其作为下一时刻参数估计值[θ]并参与到下一时刻的系统输出预报值[y（k）]计算中。依次不断循环迭代至准则函数取最小值时为止。此时，最终系统输出预报值[y（∞）]和系统真实输出值[y（∞）]最为逼近，获得此时参数估计值[θ（∞）]作为最终参数辨识结果。

其参数辨识原理如图1所示。

2 最小二乘法与最优控制方法

2.1 最小二乘算法辨识基础

大约在1795年，高斯在其著名的星体运动轨道预报研究工作中提出了最小二乘法。由于最小二乘法原理简明、易于理解、易于编程，且收敛较快，逐渐成为估计理论的奠基石，在参数估计中应用甚广。但在水轮机模型参数辨识问题上，最小二乘法的应用不多。本部分简要介绍最小二乘辨识算法基本原理。

考虑上述扩展自回归模型（ARX），若系统模型是传递函数形式，将其转化为形如ARX模型的形式，再将其转换为最小二乘形式。对于单输入单输出（SISO）的数学模型：

一般辨识既要确定模型结构，即确定阶次n，也要确定参数[ai，bi]，即辨识出参数。本文讨论结构参数n和d均已知的情况，即模型结构已知情况下仅对参数进行辨识。

将式（12）写成最小二乘形式。

其中，β为测量总次数，一般来说测量总次数β应远大于待估参数的数量。当J为最小值时的参数估计值，[θ]即为最小二乘参数辨识结果。要求得J的最小值，即为求极值问题，使J对[θ]的求导为0。

式（17）即为所要构造的目标函数。当[Φ]满秩时，观测矩阵[Φ]不是一个方阵，但[ΦTΦ]是一个方阵，[Φ]满秩，[ΦTΦ]为可逆矩阵，故容易求得：

而且此时的J对[θ]的二阶导数大于0，J对[θ]的二阶导数为：

故[θ]正是最终要求辨识出的参数值。

其中，Y为β组输出的列向量矩阵形式，[Φ]为输入输出矩阵φ的列向量矩阵形式。

本文采用的是离线辨识方法，即采集到所有需要的输入输出数据（基于模拟样本数据）后对数据用批处理最小二乘法进行集中处理。

2.2 最优控制方法在参数辨识中的应用及流程

最优控制器在优化控制系统控制参数上有较广泛的应用，参数辨识问题属于控制领域研究范畴，故将其应用到模型参数辨识问题上是有依据的。

参数辨识问题和控制问题在实质上均可以转换成寻优问题，即目标误差函数取最小值时求得需要的参数值。基于数值最优化技术的最优控制器设计方法不拘泥于传统最优控制格式，目标函数可以任意定义，因此应用前景更好。参考薛定宇教授[13]提出的基于跟踪误差指标的最优控制器设计程序，用MATLAB与其中的Simulink模块求得参数最优辨识值。用Simulink搭建待辨识模型与原真实模型的并联系统，附加原系统模型给定的阶跃扰动和噪声作为输入模拟真实系统，将附加待辨识模型给定的阶跃扰动作为输入。其中，待辨识模型允许将待辨识参数设为未知数a1、a2等格式。将待辨识系统的输出与原真实系统模型的输出连接，并求误差给ITAE模块。ITAE准则即为时间乘以误差绝对值积分的误差积分准则，需要估计ITAE指标收敛时间并将其作为参数辨识过程的仿真时间。理论上应该选择正无穷的时间作为仿真时间，但显然不符合实际情况。经研究表明，选择ITAE曲線进入稳态后的时间1～2倍以内均可满足仿真要求，对待辨识参数值的影响不大，且时间选取过长将影响暂态结果。

在仿真过程中，Simulink模块搭建完成后，需调用OCD最优参数辨识对话界面程序，将Simulink模块名输入模型栏，将待辨识参数名输入至参数栏，可根据人为约束设定待辨识参数上下界，设定仿真时间，在仿真时间内，OCD程序会不断改变待辨识参数值，使得ITAE指标持续地满足需求，即实际系统模型输出与含待辨识参数的系统模型输出不断逼近一致。设定仿真时间截止或ITAE指标满足要求时，可得出待辨识参数具体值。

3 模型参数辨识举例验证

3.1 实测数据获取

由于电站实测数据较难获取，因此本文用仿真方法获取替代实测响应数据。采用Simulink建立仿真数据采集模块。

用阶跃响应外加一定量噪声干扰当作水轮机输入数据，导入workspace2，获取水轮机输出响应数据（功率）替代实测输出响应数据并导入workspace1。数据如图3所示。

对理想水轮机模型进行辨识。理想水轮机数学模型如式（9）所示。在参数待辨识模型的辨识中采取的输入输出数据如图3所示，对辨识后模型输出和原真实系统模型输出数据进行对比时，真实系统模型和辨识后系统模型均采用相同的阶跃扰动，外附加小噪声输入激励。

3.2 批处理最小二乘法参数辨识

运用最小二乘法，根据实测输入输出数据辨识Tw参数值。对理想水轮机传递函数模型进行拉普拉斯反变换，得到式（21）。

引入白噪声序列 [xi]，运用批处理最小二乘法，根据实测（样本）数据，对待辨识模型进行参数辨识并计算其误差，对辨识结果进行评价。

输入只给定阶跃扰动的辨识后模型输出响应与实测输出响应关系，如图4所示。

实测（样本）与最小二乘辨识误差曲线如图5所示。

求得均方根误差为0.034 4，平均绝对百分比误差为0.076 9，且从图5可以看出，辨识后响应和实测响应在一定程度上比较贴切，能在较短时间内实现基本逼近。该方法不仅容易实现对线性系统模型参数的辨识，而且能达到较好的辨识效果。

3.3 基于OCD程序与ITAE准则的参数辨识

搭建可以实现参数辨识的Simulink模块，如图6所示。

其中将待辨识参数值设定为a1、a2。将模拟实际系统模型的输出与含待辨识参数的模型输出作为误差给误差积分准则ITAE模块。

调用OCD程序，打开人机对话界面，如图7所示。

输入Simulink模块名，输入待辨识参数变量名，根据经验设定待辨识参数值上下界作为人为约束，设定仿真时长，点击Create File按钮，继续连续点击Optimize按钮，即可让Simulink模块参与OCD程序参数辨识训练，得到最终仿真结果和待辨识参数值。

得到a1、a2分别为-1.974 1、0.972 9，易分离得到Tw值为1.96。得到实际系统模型和辨识系统模型输出曲线如图8所示。

实际系统输出与辨识系统输出误差曲线如图9所示。

得到均方根误差为0.008 3，平均绝对百分比误差为0.018 4。可见误差明显低于最小二乘法辨识结果，辨识精确度更高。

将最小二乘法与基于OCD程序和ITAE准则的辨识结果进行比较，如图10所示，从中可直观地看出OCD辨识结果比最小二乘的辨识仿真结果更贴合实际（样本值），但最小二乘辨识结果响应速度更快。

4 结语

本文探讨了批处理最小二乘法与基于数值最优化技术的最优控制方法对实测数据（样本）的参数辨识效果，通过参数辨识后得到的输出功率与现场实测输出（样本）具有较高的拟合度。批处理最小二乘法能够实现较好的线性辨识效果，可较容易地获取辨识后参数具体值，且操作简便。基于数值最优化技术的最优控制方法辨识结果较最小二乘法具有更高的与实测数据拟合度。基于数值最优化技术的最优控制方法先对待辨识传递函数模型进行差分方程变换，而后运用批处理最小二乘法进行精细辨识，符合模型参数辨识数学步骤，再参考得到线性模型参数辨识的人机交互界面，避免底层程序编程，根据输入输出实测数据进行参数辨识。该方法具有一定的普适性和参考价值。

以上两种辨识方法对基于实测（样本）数据的线性系统模型参数辨识有良好的仿真结果，参数辨识值与原系统参数值逼近，验证了其对给定实测输入输出数据的真实系统在小范围波动下，在近似线性化模型参数精细化辨识上具有可行性。参数辨识后得到的模型可替代真机模型进行仿真研究工作，可得到符合实际系统期望的模型。下一步将对非线性系统模型参数辨识进行研究，验证OCD人机界面应用于非线性系统辨识的可行性。

参考文献：

[1] 陈志环. 水轮机调节系统的参数辨识与控制策略研究[D]. 武汉：华中科技大学，2017.

[2] 丁聪，把多铎，陈帝伊，等. 混流式水轮机调节系统的建模与非线性动力分析[J]. 武汉大学学报：工学版，2012，45（2）：187-192.

[3] 彭伊丽. 用于水电控制仿真中的水轮机模型辨识[D]. 武汉：华中科技大学，2011.

[4] 华中科技大学. 一种水轮机调节系统的参数辨识方法：CN201510759863.1[P]. 2016-02-03.

[5] 高晓光，唐戢群，刘德发，等. 水轮机及调节系统模型辨识试验研究[J]. 人民长江，2016，47（13）：84-89.

[6] 方日升. 水轮机引水系统精细化模型参数辨识研究[J]. 电力与能源，2018，39（2）：261-265.

[7] DEMELLO F P，KOESSLER R J，AGEE J，et al. Hydraulic turbine and turbine control models for system dynamic studies[J].? IEEE Transactions on Power Systems， 1992， 7（1）：167-179.

[8] 张记坤，曾云，王芳芳，等. 混流式水轮机调节系统非线性建模与分叉分析[J]. 软件导刊，2019，18（12）：102-107.

[9] 张楚. 抽水蓄能机组调节系统非线性辨识与优化控制研究[D]. 武汉：华中科技大学，2018.

[10] 吴凡，李伟雄. 基于MATLAB系统辨识工具的系统辨识[J]. 河北农机，2016，（11）：59-60.

[11] 陈岚峰，张亚琴，程立英，等. 基于数据的MATLAB系统辨识工具箱模型识别[J]. 沈阳师范大学学报（自然科学版），2013，31（4）：527-530.

[12] 庞中华，崔红. 系统辨识与自适应控制MATLAB仿真（修订版）[M]. 北京：北京航空航天大学出版社，2013.

[13] 薛定宇. 控制系统计算机辅助设计-MATLAB语言与应用（第3版）[M]. 北京：清华大学出版社，2012.

[14] 卢志强. 连续时间系统课程的离散化方法综述[J]. 中国科教创新导刊，2010，（34）：85-86.

[15] 王贞祥，高立群，李玮，等. 系统辨识与参数估计[M]. 沈阳：东北大学出版社，1993.

[16] 李伟，王洪民，唐峥. 基于递推最小二乘法的转向系统参数辨识[J]. 重庆交通大学学报（自然科学版），2019，38（8）：124-128.

[17] 张国洋. Matlab在水轮机模型辨识中的应用[J]. 自动化应用，2016（1）：19-20，26.

[18] 黄莉，李咸善. 基于Simulink的水轮机动态仿真模型研究[J]. 三峡大学学报（自然科学版），2007，29（1）：25-28.

[19] 吴卓璠. 水轮机调节系统非线性建模与参数辨识[D]. 武汉：华中科技大学，2016.

[20] 刘昌玉，梁学磊. 水轮机调节系统被控对象模型辨识[J]. 水电能源科学，2007，25（2）：77-79.

[21] 柳海生，曾江，黃海颖，等. 抽水蓄能电站水泵水轮机效率计算方法[J]. 广东电力，2014（9）：1-5.

（责任编辑：江艳）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。