网站首页  词典首页

请输入您要查询的论文：

　

标题 重型立式车床底座热场与自然对流换热特性
范文 杨晓冬 刘红博 刘祥彬 金朝晖



摘 要：重型数控立式车床的底座是保证机床稳定性和精度的核心部件之一。针对机床转速提高引起的底座热集中问题，为探明机床转速提高对底座热场和散热的影响，依据传热学和流固耦合力学建立了重型立式车床底座的对流换热数学模型和流固耦合热场模型。通过对重型数控立式车床的底座热场模型进行数值模拟，揭示了机床底座的热传递规律，探明了转速对底座热场和换热强度的作用。流固耦合数值模拟结果与数学模型结果对比结果表明两者基本吻合，为重型数控车床底座的设计和分析提供了有价值的理论依据。
关键词：
重型立式车床；热场；流固耦合；对流换热
DOI：10.15938/j.jhust.2018.03.023
中图分类号： TH133.36
文献标志码： A
文章编号： 1007-2683（2018）03-0133-06
Natural Convection and Thermal Field Numerical
Simulation of Heavy-Duty Vertical Lathe Base
YANG Xiao-dong1， LIU Hong-bo1， LIU Xiang-bin2， JIN Zhao-hui3
（1.School of Mechanical Engineering， Harbin University of Science and Technology， Harbin 150080， China；
2.Repack Flight Personnel for Bomber and Carrier， 93199 Troops of the PLA， Harbin 150000， China；
3.CRRC Qiqihar Rolling Stock CO.， LTD. Qiqihar 161000， China）
Abstract：The base of heavy-duty CNC vertical lathe is one of the core components to ensure stability and precision of the lathe. Aiming to the issue of heat concentration internal structure of lathe-base， to verify the influence that velocity increasing impacts on heat generate and heat dissipation， convection mathematical model and FSI （fluid-solid-interaction） heat transfer model of the base of heavy vertical lathe was established according to heat transfer theory and fluid-solid-interaction theory. The results of numerical simulation of heat transfer model of the base reveal the heat transfer regularity and the influence of velocity that impacts on thermal field， heat dissipation intensity of the base. Comparison result between FSI numerical simulation results and mathematical model results show that they are basically consistent. It provides a valuable theoretical basis for heavy-duty CNC vertical lathe design and analysis.
Keywords：heavy-duty vertical lathe； thermal field； fluid-solid-interaction； convection heat transfer
0 引 言
重型立式车床主要服务于水电核电、航空航天、舰船制造和国防工业等国家重点行业，是重型制造行业的主要加工设备，尤其对于大半径旋转曲面类零件的加工，有着独特的优势。20世纪30年代德国Salomon博士提出了高速切削理念，其意义不仅在于提高生产效率，工艺性、能耗和表面粗糙度都会改善，高速切削技术逐步成为切削加工的主流技术是大势所趋[1]。提高立式车床转速的过程中出现了一些问题，车床转速提高会使静压轴承发热加剧，造成热集中，引起车床的热变形，导致机床精度降低，严重时甚至使轴承的实际结构偏离理论设计模型。因此如何在保证机床本身的精度和稳定性的前提下提高转速，成为了目前亟需解决的关键问题之一，而掌握重型立式车床的发热与散热规律则是解决问题的前提[2-3]。
立式车床的车削加工主要依靠其工作台旋转，工作台包括花盘，底座和两者间隙形成的润滑油膜，以及驱动装置。花盘主要起承载和装夹工件的作用，安装在底座中心的定心轴承上，定心轴承为双列圆柱滚子轴承，不承受轴向力，花盘和工件的重量依靠底座承担。而机构运转的摩擦力巨大，仅靠常规润滑形成的油膜无法勝任[4]。目前立式车床普遍采用液体静压润滑，花盘的镜板（承压面），油膜和底座的油垫构成了静压推力轴承。静压推力轴承依靠外力向油腔内供给恒定压力的润滑油、利用腔内与大气间的压力差，在油腔内和封油边上形成具有很高压力的油膜，形成静压推力轴承的承载力，浮起花盘并能承受更多外载荷，使花盘始终悬浮在油膜上。液体静压轴承广泛应用于要求严格或高精度的高低速回转机构中，作为回转类大重型设备的核心部件，具有其他类型轴承不可替代的优势[5，6]。
发达国家在20世纪中叶开始推广在重型设备中使用静压润滑技术，我国从50年代后期开始液体静压轴承的应用研究工作，近几年静压技术迅速的发展，并逐步完善和成熟，研究不断深入。很多针对静压轴承进行了很多深入的研究，包括静压轴承的承载性能[7]，润滑介质特性[8]，发热特性[9，10]和油膜流态等，静压轴承结构的研究方面包括静压轴承的油腔结构[11-13]，节流器结构[14-15]和控制系统[16]等。静压轴承的应用范围逐渐扩大，几遍及整个制造业、军工和民用设备上。车床底座的实际散热条件并不理想，主要依靠外表面与环境空气对流换热，如图1所示为DVT500型系列机床，静压推力轴承导轨直径为2500mm，工作台直径4500mm，最大加工直径5000mm。超大型数控立式车床因为空间限制或装卡工件的需要，安装高度与地表平齐或略高于地表，工作台的大部分表面都无法和外界直接接触，很大程度上限制了散热效果。而散热不均造成的温差会造成热变形，对静压轴承工作性能的影响更恶劣[17]。
1 机床底座对流换热数学模型
对于二维稳态自然对流换热问题，为建立散热表面与环境空气的关系，表达散热表面温度加热空气时造成的空气密度变化，引入体积膨胀系数β=-1/ρρ/TP，密度变化产生的浮生力可表示为[18]
Fρ=ρf-ρg=ρβΔTg（1）
则根据强制对流换热动量方程，自然对流换热动量方程可写为
uux+vuy=gβΔT+ν2uy2（2）
对式（2）进行相似性分析并无量纲化（标*为无量纲量）可得
u0lνu*u*x*+v*u*y*=gβΔTl2νu0T-TfTs-Tf+ν2u*y*2（3）
由式（3）可得以衡量自然對流换热过程中浮生力与粘滞力的关系。与Reynolds数反映流动系统中Re数相等的原则同理，Grashof数（以下简称Gr数）是自然对流流态层流紊流转变规律的参考值，Gr越大表示浮生力作用越大。
Gr=gβΔTl2νu0u0lν=gβΔTl3ν2（4）
式中：g为重力加速度，9.8m/s2；l为特征长度，对于竖壁或竖圆柱为高度，横圆柱取外径；ν为空气在温度为Tm时的运动粘度。
所以对于底座空气自然对流换热，式（4）可表示为
Gr=gβΔTl3ν2=gβΔTπr23/2ν2（5）
Nu数可表示为Gr数的函数，可表达为
Nu=fGr，Pr=CGrPrn（6）
对于水平散热表面，对自然对流换热的能量守恒方程进行相似性分析和无量纲化，可导出Gr数与Pr数的关系式，导出的无量纲量为Rayleigh（缩写Ra）数，目前一般以水平散热表面空气的Ra数作为判断流态转变规律的参考值，可表示为
Ra=gβΔTl3aν=GrPr（7）
式中：α为热扩散系数，α=k/ρc，单位为m2/s。
根据圆盘类零件的对流换热规律得出了花盘顶面的强制对流换热规律和自然对流换热规律，自然对流类型按换热面的方向可分为：竖直、向上和向下，表面类型包含平板或圆柱等。根据大量典型实验确定的C和n的值及适用范围如表1所示，由式（6）得到Nu数分析对流换热强度。
静压推力轴承的油膜产生的热量是底座的主要热源，包括液压油携带的热量、系统发热等，另外花盘的驱动装置等配套部件安装在底座上，这些部件也会产生一定的热量，所以底座实际受热情况比较复杂。底座作为主要部件之一，除花盘外，立柱、减速器、电机、油泵等均装配在底座上，电机油泵等均配备散热装置，所以底座散热条件也非常复杂。为研究静压轴承系统发热和转速对底座热场的影响，假设润滑油膜发热为底座的唯一热源。
底座可靠地安装在混凝土地坪上，机床的底座的底角区域与混凝土良好接触，并可靠的固定，目的是提高机床的抗震性和刚度。底座无法转动，只能靠自然对流散热，散热能力有限。如图2所示，底座散热依靠其外缘的表面，主要为自然对流，包含了三种自然对流类型，共有三种自然对流换热类型：区域1、3为竖圆柱（平板）上表面自然对流换热；区域2为热面向下平板自然对流换热。
边界条件
采用Workbench平台对车床底座的流固耦合问题进行数值模拟。流固耦合同时涉及流体和固体求解器，均可在Workbench平台中实现，涉及到的模块有几何建模模块、网格划分模块、CFD模块，固体分析模块等。
2.1 假设条件
1）车床底座的定心轴承和驱动装置的发热量远小于静压油膜的发热量，为研究油膜发热对工作台热场的影响，假设油膜发热为唯一热源；
2）润滑油即使在高压下的压缩性也极其微小，假设润滑油为不可压缩流体，且忽略固体表面粗糙度对流体的影响；
3）假设环境温度基本恒定，任一温度值下环境空气物性为恒值。
2.2 边界条件
静压轴承采用定量供油方式，油泵输出最大流量60L/min，经12头分油泵分油。一般认为间隙油膜出口位置回流微小，设为单向出口。入口设为质量流入口，温度为环境温度，空气域不设入口，出入口边界均设为开放出口。根据车床底座对油膜厚度的要求，可得空载机床在转速为50r/min、环境温度为25℃左右时，可将油膜厚度维持在100μm左右的流量为14.658×10-3kg/s。
静压推力轴承的润滑介质为通用型机床工业润滑油，牌号为L-HL46，主要参数如下：密度为0.875g/ml，比热容1884J/（kg·K），导热系数为0.132W/（m·K），粘度指数105。车床的底座是典型大型铸造件，根据承载能力级别和尺寸使用不同的材料和铸造形式。本机床属于中型机床，材料为HT250，密度7300kg/m3，比热容50.25J/（kg·K），导热系数为523.36W/（m·K）。静压轴承油垫材料采用了具备较好耐磨性和导热性的高硬度铝合金2A12，密度2780kg/m3，导热系数193W/（m·K），比热容924J/（kg·K）。
固体域采用有限元法，流体域采用有限体积法，全隐式求解流固耦合方程，在考虑润滑油粘温关系和空气浮力流的情况下，模拟了供油流量为14.658×10-3kg/s环境下，车床底座逆时针旋转，转速范围在5～50r/min内的车床底座热场，包括静压油膜流场，固体的温度场、空气流场及其对散热情况的影响。静压油膜网格单元总数为439942，底座网格数量为142706，油垫网格数量为73700，网格收敛性检查全部通过，符合计算要求。
3 重型立式车床底座数值模拟
3.1 静压推力轴承发热特性
图3和图4为静压油膜温度场云图。总体温度值随转速升高而提高，静压油膜温度场外缘为高温区，线速度越大剪切发热越严重，可见润滑油的剪切流动是发热的主要原因之一。油腔内部的油温偏低，说明油腔内部存在环流，使入油口的低温润滑油在油腔内部持续地流动。转速为25r/min时开始出现扰流，低温区域开始扩大，环流和扰流均随转速的提高逐渐加剧。车床底座逆时针旋转，低温润滑油自下游侧流出油腔，使下游侧温度偏低。油液携带效应将上游相邻油垫的低温润滑油卷入，转速升高时（大于10r/min）使上游侧温度仍比油膜内缘温度低，且随转速提高该低温区域逐渐扩大，可见油液携带效应在高速下不可忽略，且随转速提高逐渐加强。
由静压轴承原理可知，工作台旋转过程中，静压油膜被迫以一定的速度在摩擦副间作剪切流动，花盘靠静压承载，且高压润滑油流出油腔后的油压为零，压力能全部由油液吸收，压力差也使润滑油作压差流动。润滑油剪切发热、动能的损耗以及压差流动发热，全部转化为润滑油的热量，一部分被润滑油流动带走，其余被花盤和底座吸收，这三种生成热都会使系统升温。润滑油升温会引起油液粘度显著变小，降低静压油膜的承载能力和可靠性。
3.2 底座热场特性
图5为机床转速为20r/min时底座温度场，其余转速的温度场分布趋势与图5类似，各转速下的温度梯度基本一致，总体温度值随转速升高而提高。底座高温部分为靠近油膜的区域，该区域随转速提高呈扩大的趋势。温度梯度沿周向筋板大致呈垂直分布，自上而下逐渐减小。低温部分为底座与地坪接触的区域。转速为20r/min时，底座最大温差为16.221℃，热集中现象更严重。出于散热和静力承载的考虑，油垫材料选用铝型材，铝合金的热膨胀系数是铸铁的两倍，热载荷会造成铝合金油垫热膨胀，对静压轴承润滑的稳定性造成不利的影响。
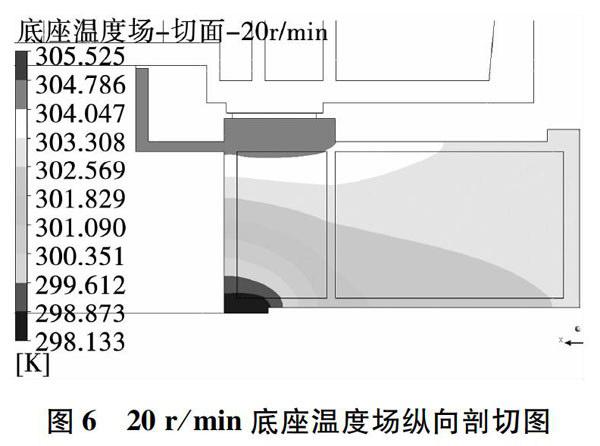
图6为机床转速为20r/min时，底座温度场沿纵向筋板的剖切视图，该图清晰地表明了底座径向筋板、周向筋板和水平筋板的温度梯度分布。
3.3 底座自然对流换热特性
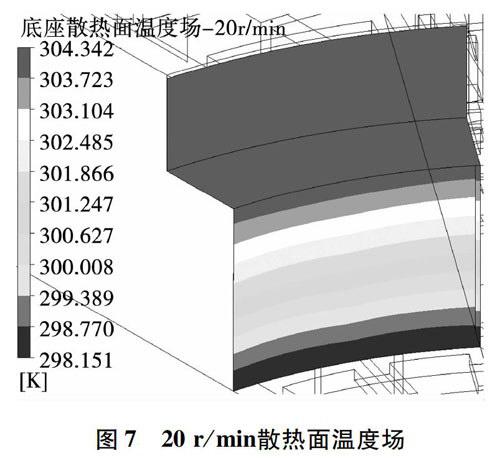
图7和图8所示分别为底座散热面的温度场和换热系数场，温度梯度随转速提高并未产生显著变化，仅温度值逐渐升高，靠近油垫的位置为高温区。对于底座散热面的热流密度场和换热系数，转速低于40r/min时，空气流态稳定，空气流态在40r/min时达到临界状态，在花盘下方已开始形成涡流，并提高了底座散热面的换热强度。45r/min后花盘下方的涡流逐渐稳定，流态转变后，筋板下端的对流换热强度增大，说明在此位置的空气流速相对加快，两者在外部筋板上的分布则趋于平衡，数值上的影响详见转速对底座散热面的曲线，如图9所示。
由图可见，转速升高时，受空气流态影响，对流换热强度发生改变，但对温度梯度分布影响不大，可见转速对底座温度梯度的影响并不剧烈。转速低于45r/min时换热强度较低，随转速提高换热强度缓慢加强，曲线在45r/min时出现拐点，花盘下方形成的涡流在底座散热面上形成了微弱的强制对流换热，使换热系数开始增加。可见在花盘下方形成的涡流虽然一定程度上减弱了花盘的对流强度，但大大加强了底座的对流强度。
如图9所示，换热系数的理论均值随转速增加增加，在45r/min时出现拐点，换热强度略微减弱。换热系数的模拟均值在转速低于45r/min时，换热强度随转速增加略有增强，且底座换热系数的理论均值高于模拟均值，45r/min时换热强度增强，高于理论值。换热系数理论均值计算依据的是数值模拟结果中提取的散热面平均温度和环境空气温度，而数值模拟中散热面附近的空气温度高于环境空气温度，温差小于理论计算，所以理论值偏高。数值模拟结果在45r/min时出现拐点说明底座附近空气流场的流态在45r/min时发生了转变，显著增强了对流强度，转速继续提高将强化底座散热面的对流，数值模拟值将高于理论值。
4 结 论
1）车床的转速对底座的温度场影响较大，转速提高在强化散热的同时也增加了结构内外的温差，导致结构的热集中现象及其造成的结构热变形更加严重。
2）车床的转速在低转速时对底座换热强度的影响并不明显，转速提高到高转速时则空气流场的流态变化距离，显著增强了底座的换热强度。
3）针对重型立式车床底座的对流换热特性，基于传热学建立了车床底座的对流换热数学模型，经验证与数值模拟结果趋势基本符合，为车床底座的散热计算提供了可靠的依据。
参 考 文 献：
[1] 艾兴. 高速切削加工技术的现状和发展[C]// 现代切削与测量工程（国际）研讨会， 成都， 2004： 15.
[2] RON A.J. van Ostayen， ANTON van Beek， MINK Ros. A Parametric Study of the Hydro-support[J]. Tribology International， 2004， 37： 617.
[3] RON A.J. van Ostayen， ANTON van Beek， MINK Ros. A Mathematical Model of the Hydro-support： an Elasto-hydrostatic Thrust Bearing with Mixed Lubrication[J]. Tribology International， 2004， 37： 607.
[4] 于晓东， 周启慧， 王志强. 高速重载静压推力轴承温度场速度特性[J]， 农业机械学报， 2014， 45（7）： 292-299.
[5] AI Xiaolao， YU Haiging. A Full Numerical Solution for General Transient Elasto Hydrodynamic Line Contact Sand it S Application[J]， Wear， 1988， 121： 143-159.
[6] 邵俊鹏. 靜压推力轴承润滑性能研究方向[J]. 哈尔滨理工大学学报， 2011， 16（6）： 1-10.
[7] ESPARZA L. F. Martinez， DE Gortari， J. G. Cervantes， UZIEL E. J. Chicurel. Design of Hybrid Hydrostatic/Hydrodynamic Journal Bearings for Optimum Self-compensation Under Misaligning External Loads[J]. Structures and Dynamics， 2016， 7B： 14-16.
[8] 李景惠， 李永海， 向敬忠. 推力轴承油槽油流态的可视性研究[J]. 哈尔滨理工大学学报， 2000， 5（2）： 56-58.
[9] KIM Bo-Sung， BAE Gyeong-Tae， KIM Gwi-Nam， et al. A Study on the Thermal Characteristics of the Grinding Machine Applied Hydrostatic Bearing[J]. Transa-ctions of the Canadian Society for Mechanical Engineering. 2015， 39（3），717-728.
[10]于晓东， 周启慧， 王志强， 等. 高速重载静压推力轴承温度场速度特性[J]. 哈尔滨理工大学学报， 2014， 19（1）： 1-4.
[11]邵俊鹏， 张艳芹， 李永海， 等. 大尺寸椭圆形静压轴承油膜态数值模拟[J]. 哈尔滨理工大学学报， 2008， 13（6）： 117-120.
[12]WONG Shih-Ming， LAI Ta-Hua， LIN Min-Cheng， et al. A Simulation Study of Recessed Type Hydrostatic Journal Bearing[C]// ICMMR 2016. Chongqing. 2016，77.
[13]于晓东， 李欢欢， 谭力.圆形腔多油垫恒流静压推力轴承流场数值分析[J]. 哈尔滨理工大学学报， 2013， 18（1）： 41-44.
[14]GOHARA Makoto， SOMAYA Kei， MIYATAKE Masaaki， et al. Static Characteristics of a Water-lubricated Hydrostatic Thrust Bearing Using a Membrane Restrictor[J]. Tribology International. 2014， 75： 111-116.
[15]SAWANO Hiroshi， NAKAMURA Yusuke， YOSHIOKA Hayato， et al. High Performance Hydrostatic Bearing Using a Variable Inherent Restrictor with a Thin Metal Plate[J]. Precision Engineering. 2015， 41： 78-85.
[16]NAKAO Yohichi， KOMORI Masataka， MAKINO Naohiro， et al. Displacement Control of Water Hydrostatic Thrust Bearing by Hybrid use of Constant Resistance Restrictors and Flow Control Valve[C]// EUSPEN 2015， Belgium， 2015： 263-264.
[17]杨晓冬， 邵俊鹏， 穆晓宁， 等. 重型立式车床转台稳态传热数值模拟与实验研究[J]， 农业机械学报， 2014， 45（7）： 292-299.
[18]杨世铭， 陶文栓. 传热学[M]. 第四版. 北京：高等教育出版社， 2006：197-227， 263-271， 273-276.
[19]HOLMAN J P. HEAT Transfer[M]. 9th ed. McGraw-Hill， 2002： 285-287.
[20]INCROPERA F. P.， DeWitt D P Fundamentals of Heat and Mass Transfer[M]. 5th ed. John Wiley&Sons;， 2002： 430， 482， 492， 546， 551.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/10 17:08:56