《非稳定渗流场对黏土心墙坝坝坡及心墙稳定的影响分析》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

非稳定渗流场对黏土心墙坝坝坡及心墙稳定的影响分析

范文

袁浩瀚焦延涛

摘要：应用三维非稳定饱和-非饱和渗流有限元法建立xx水库枢纽区的三维有限元模型，对极端工况条件下（v=4.42m/d）坝体的非稳定渗流场进行了计算分析，结果表明1d内库水位由校核洪水位骤降至汛限水位，不会对坝坡及心墙的稳定造成不利影响。

Abstract： The three-dimensional unsteady saturated-unsaturated seepage is used to establish a three-dimensional finite element model of the xx reservoir pivot area. The unsteady seepage field of the dam under extreme conditions （v=4.42m/d） is calculated and analyzed. The results show that the water level in the reservoir within one day is suddenly reduced to the limit water level by the check flood level， which will not adversely affect the stability of the dam slope and the core wall.

關键词：三维非稳定饱和-非饱和渗流有限元法;非稳定渗流场;坝坡

Key words： three-dimensional unsteady saturated-unsaturated seepage finite element method;unsteady seepage field;dam slope

中图分类号：TV641;TV223? ? ? ? ? ? ? ? ? ? ? ? ? ?文献标识码：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章编号：1006-4311（2019）34-0248-03

0? 引言

坝坡稳定是土石坝设计的一个重要组成部分。当库水位骤降时，坝体内浸润线高于坡外库水位，较高的孔隙水压力和渗透力会使上游坝坡具有下滑趋势，甚至酿成滑坡事故[1-4]。据资料，土石坝占各类大坝总数的82.9%，在各种土石坝垮坝事故中，因渗漏原因垮坝的高达29.1%，其中因为水位骤升骤降引起的非稳定渗流问题最为严重[5]。有鉴于此，本文以xx黏土心墙坝为研究对象，应用三维非稳定饱和-非饱和渗流有限元法对该黏土心墙坝在极端情况下（水位骤降速度4.42m/d）的非稳定渗流场进行了模拟分析，探讨水位骤降对该坝坝坡稳定的影响。

1? 工程概况及基本资料

xx水库位于xx省宜良县汤池镇曲者村附近摆夷河左岸一级支流白金龙箐下游河谷地段，水库主要功能和任务是解决汤池镇曲者、可保2个村委会的集镇、农村人饮，同时兼顾下游灌溉。水库工程规模为小（1）型，水库设计洪水位1882.89m，校核洪位1884.31m。大坝为粘土心墙坝，大坝坝轴线设计全长为164.8m，大坝坝顶高程设计为1884.40m，大坝坝顶设混凝土防浪墙，防浪墙高1.2m，大坝坝顶设计宽度为5m。坝顶下游侧设有路缘石，路缘石高出坝面0.2m，防浪墙和下游路缘石均采用C20混凝土。坝顶路面采用C30现浇混凝土路面，下设20cm厚碎石垫层。大坝典型剖面如图1所示。

2? 三维有限元模型

2.1 计算模型范围

以大地坐标（507080.895，2765817.504）为模型坐标原点;取垂直于坝轴线方向为X轴，X轴正方向指向大坝下游;取平行于坝轴线方向为Y轴，Y轴正方向指向大坝左岸;取竖直方向为Z轴，Z轴正方向向上。计算模型上游截取边界为坝轴线向上游延伸约179m（X=-179m），下游截取边界为坝轴线向下游延伸约172m（X=172m），左岸截至距离左坝端100m（Y=264.8m），右岸截至距离右坝端85m（Y=-85m），底边界截取至高程1760m，顶边界截至顶高程1884.4m。按照上述范围建立大坝模型，离散后有限元网格结点总数为26183个，单元总数为24280个，三维有限元模型网格如图2所示。

2.2 模型边界条件

计算模型的边界：①坝址区上游及下游水位淹没线以下部分为给定水头边界;②坝址区上游及下游水位淹没线以上与空气接触的部分为出渗边界;③不透水边界为模型四周及模型底面边界。

3? 计算参数和时间步长的选取

3.1 计算参数选取

进行土坝的非稳定渗流计算时，除了需考虑材料的渗透系数外，还需要给定材料的给水度[5]。本文计算所需材料参数如表1所示。

3.2 时间步长确定

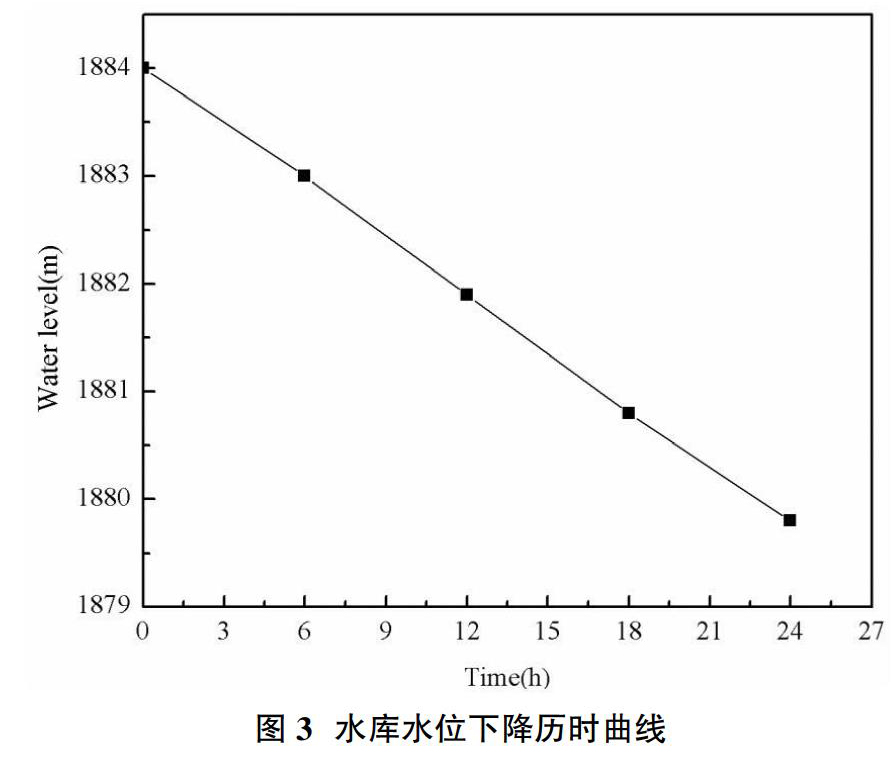
渗流计算中，时间步长的取值不宜过大也不宜过小，时间步长取的太小容易导致过大的累积误差，而取的太大将会导致计算不易收敛[5]。经过试算，最终确定时间步长为0.25d，则水库水位在24h内由校核洪水位1884.31m骤降至汛限水位1879.89m的水位下降历时曲线如图3所示。

4? 计算成果分析

采用前文所述的三维有限元模型，对xx水库在水位降落速度为4.42m/d条件下的非稳定渗流场进行计算，计算得到坝体典型剖面Y=94.8m在0h、12h和24h三个不同时刻等势线图如图4所示。

衡量库水位降落影响的指标一般采用比值（k/（μv）为渗透系数，μ为介质的给水度，v为库水位下降速度），此比值反映了介质孔隙中水体降落速度与库水位降落速度之间的关系，也可以用于判别库水位降落速度对坝坡稳定性的影响，当k/（μv）<1/10时，自由面下降极缓，属于骤降;当k/（μv）>10时，孔隙水和库水位同步下降，随之泄尽，渗流对稳定性没有影响;当1/10

4.1 坝壳渗流性态

从图4可以看出，在库水位降落过程中，上游风化料坝壳内的自由面基本与库水位同高。风化料坝壳的渗透坡降很小，不会对上游坝坡稳定造成不利影响。而下游风化料坝壳内的自由面水位变化很小，坝壳内的渗透坡降也较小，不会对下游坝坡的稳定造成不利影响。

4.2 心墙渗流性态

心墙的渗透系数为1.00×10-8m/s，给水度为4×10-3，库水位下降速度为4.42m/d，相应比值约为4.89×10-2，因此该水库水位降落速度属于骤降。在库水位降落起始时刻（t=0），心墙上部的最大渗透坡降约为2.4，随库水位的降落，最大渗透坡降减小。库水位降落至正常蓄水位1879.89m时，心墙上部的最大渗透坡降约为1.2。在库水位下降过程中，心墙上部自由面较起始时刻（t=0）明显平缓，但心墙内自由面最高点仍低于库水位，即在水位下降过程中渗透力总是由上游指向下游且逐渐减小。因此，不会对心墙的稳定造成不利影响。

5? 结论

①在库水位降落过程中，大坝上下游风化料坝壳内的渗透坡降均很小，不会对上下游坝坡稳定造成不利影响。

②在极端工况下（v=4.42m/d），粘土心墙上部的最大渗透坡降小于允许渗透坡降，且心墙内自由面最高点仍低于库水位，即在水位下降过程中渗透力总是由上游指向下游且逐渐减小。因此，不会对心墙的稳定造成不利影响。

参考文献：

[1]贾苍琴，黄茂松，王贵和，等.水位骤降对土坡稳定性的影响分析[J].同济大学学报（自然科学版），2008（03）：304-309.

[2]王学武，许尚杰，党发宁，等.水位骤降时的非饱和坝坡稳定分析[J].岩土力学，2010（09）：2760-2764.

[3]刘钊，柴军瑞，陈兴周，等.库水位骤降时坝体渗流场及坝坡稳定性分析[J].西安理工大学学报，2011（04）：466-470.

[4]王资欢，张晓峰.库水位骤降对黏土心墙坝坝坡稳定的影响分析[J].水利建设与管理，2016，36（09）：42-45.

[5]贾静，沈振中，俞凯加，等.冲久水库初次蓄水大坝非穩定渗流场特性分析[J].水电能源科学，2009，27（02）：65-67.

[6]顾慰慈.渗流计算原理及应用[M].北京：中国建材工业出版社，2000.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。