《空间刚性锥体目标进动特性分析》-工学论文，通信论文-论文范文参考-科学狗论文网

标题

空间刚性锥体目标进动特性分析

范文

宋扬

【摘要】对于空间进动刚性锥体目标，本文对目标回波的频域和时频域进行了推导和分析，并对推导结果进行了仿真实验，验证了回波特性的准确性。

【关键词】进动锥体傅里叶变换时频变换

一、引言

空间锥体运动目标在飞行时往往伴随着一定的微运动。根据刚体姿态动力学的知识，刚体自旋时如果有横向干扰刚体将产生进动。进动刚性锥体目标的建模及回波特性分析是以后空间群目标分辨和识别的基础，所以非常有必要研究这种空间复杂运动目标的模型和回波特性。

二、空间刚性锥体目标建模

首先以锥形目标为例建立目标运动模型如下图：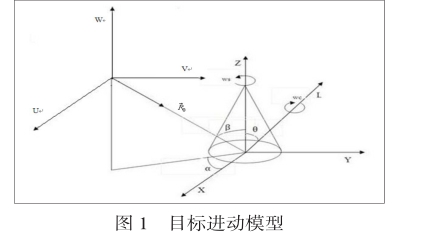

如图1所示，设目标坐标系为（X，Y，Z），雷达坐标系为（U，V，W），两坐标系平行，雷达视线在目标坐标系中的俯仰角和方位角分别为（α，β）；目标坐标系原点在雷达坐标系中的距离矢量为0R？，目标相对雷达的径向平动速度为v？，平动加速度为a；目标以ws的角速度绕Z轴自转，同时绕L轴以的wc角速度锥旋，L轴与Z轴的夹角为θ，锥体上某一散射点s在参考坐标系中的位置向量0r？为[x0 y0 z0]T。

由于进动是两种运动的叠加，因此自旋是锥旋出现的条件，要先于锥旋产生。下面就此进行分析，推导散射点的瞬时微多普勒频率。

可以看出谱线出现在nws +mwc这些频率点上，其中，m，n为整数。若ws ，wc均为互质整数，则其离散傅里叶变化后的谱线几乎出现在所有整数频率点。

由于傅里叶变化为线性变化，因此可以看出，散射点数目的增加不会引入新的频率分量，故谱线的位置不因散射点的数目增多而增加。

3.2进动锥体目标回波的时频分析

时频分析的主要研究对象是非平稳信号或时变信号，主要的任务是描述信号的频谱分量随时间的变化。短时傅立叶变换的基本思想是用一个时间宽度足够窄的固定的窗函数乘时间信号，使取出的信号可以被看成平稳的，然后对取出的这一段信号进行傅立叶变换，便可以反映出该时间宽度中的频谱变化规律，如果让这个固定的窗函数沿着时间轴移动，那就可以得到信号频谱随时间变化的规律了。

短时傅立叶变换定义如下：

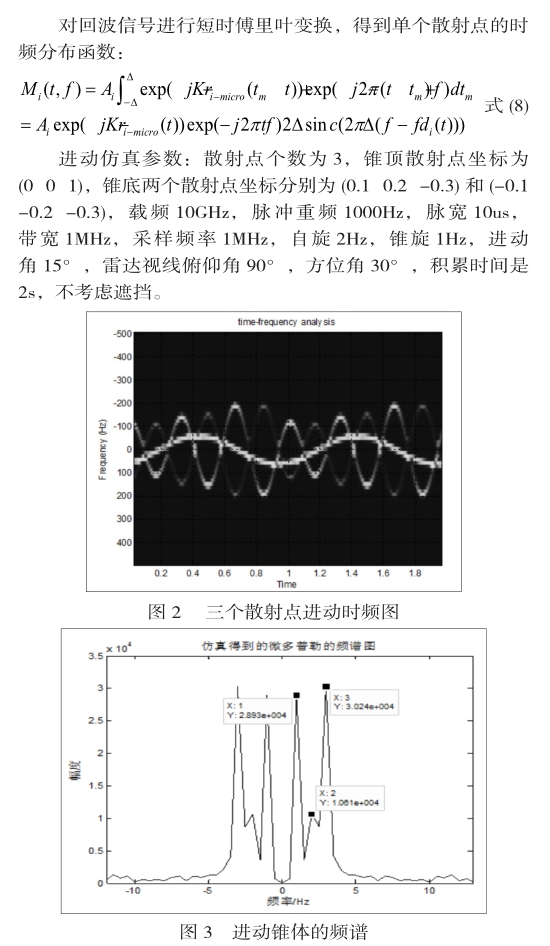
仿真结果分析：各散射点的瞬时多普勒在时频图上的分布特征是不同的。图2可以估计自旋频率：2Hz；中间那条频率为1Hz的曲线应该是锥顶散射点锥旋产生的。图3是多普勒谱，其中正频率轴上有三个强的分量，分别为进动的锥旋频率1Hz，自旋频率2Hz，自旋+锥旋频率：3Hz；仿真表明，公式（6）估计的f（t）能较准确地表示多散射点的微多普勒的线性和。

四、结束语

本文讨论了进动刚性锥体目标，推导了复杂运动弹头的瞬时多普勒频率的表达式。然后以线性调频信号为例，推导目标回波表达式，并分析了复杂运动目标回波的频谱特性和多普勒谱特性，进行了仿真验证，对空间锥体群目标的分辨和识别具有极大的研究意义。

参考文献

[1] 王璐. 微动目标的运动参数和识别方法研究. 硕士学位论文. 西安电子科技大学， 2010年1月。

[2] 符婷. 基于多普勒特征的目标分类方法研究. 硕士学位论文. 西安电子科技大学， 2011年1月。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。