网站首页  词典首页

请输入您要查询的论文：

　

标题 巧设计重体验促感悟
范文 陈香


[摘 要] 心理学研究表明，亲身经历动手操作、思考与交流，有利于加深学生对数学知识的理解与记忆. 本文结合“圆周角”课堂教学实践，阐述通过优化教学设计，让学生充分体验数学结果的形成过程，让学生主动参与活动，在活动中积极探索与发现，亲身体验与实践，经历数学概念与数学规律的形成过程、思想方法的提炼过程，感悟数学内涵.
[关键词] 初中数学；教学设计；过程体验
《义务教育数学课程标准》（2011版）明确指出：“课程内容不仅包括数学的结果，也包括数学结果的形成过程和蕴含的数学思想方法. ”因此，我们需要不断优化教学设计，注重让学生体验数学结果形成的过程，在活动过程中感悟数学思想，积累数学活动经验.
在一次教研活动中，笔者执教了苏科版《义务教育课程标准试验书·数学》九年级下册《圆周角（第一课时）》一课. 在磨课时，和同组的教师多次讨论，对教学设计进行了优化，设置了以学生为主体的活动，让学生在活动中体验圆周角概念的形成过程，主动探究圆周角的性质，领悟分类、转化、特殊到一般的数学思想，现结合本节课谈谈自己的思考.
教学过程简录
1. 情境引入
（1）我们学过一种与圆有关的角，是什么角呢？（圆心角）
（2）今天我们来研究与圆有关的另外一种角，叫圆周角，类比圆心角的概念，你能猜出什么叫圆周角吗？
设计说明 设置简单明确的情境，利用学生已有的数学知识经验，设置了有较强数学味的问题情境.
2. 概念建构
（1）你能画一画这样的角吗？
（2）你能把画的这些角分类吗？
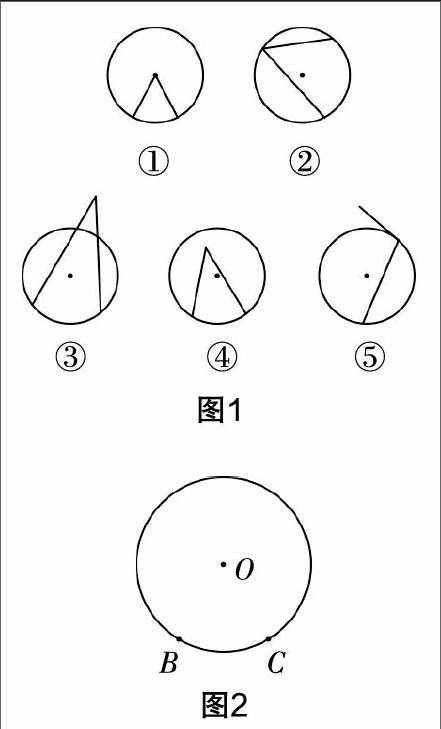
（3）判断下列图形（图1）中的角是否为圆周角，并说明理由.
（4）你能总结一个角是圆周角需要满足的条件吗？
设计说明 类比圆心角的概念，建构圆周角的概念. 设置画图、观察、思考等活动，让学生在活动中体验圆周角概念的建构过程. 通过画图形成圆周角的感性认识，通过观察、思考、分类，深刻体验圆周角概念的形成过程. 活动设计加强了学生对概念的深入理解，深刻体会到圆周角必备的两个条件，并感悟到分类的数学思想.
3. 性质探究
学习圆心角时，我们研究了圆心角的哪些性质？类比圆心角的性质，猜想圆周角具有哪些性质. 探究活动如下：
（1）如图2，请画出☉O中所对的圆心角和圆周角，可以多画几个.
（2）观察所对的圆周角有几个，你有什么发现？
（设置开放性问题，让学生在独立思考的基础上小组讨论，全班交流，引导学生从数量、位置、大小的角度进行考虑）
（3）猜想所对的圆周角与圆心角之间有什么关系.
（引导学生思考，当弧所对的圆周角有无数个时，圆心角只有一个，这无数个圆周角能否进行分类呢？如何分类？以什么标准分类呢？它们和圆心角有什么关系呢？先从哪一类开始研究呢？）
（4）试说明你的猜想.
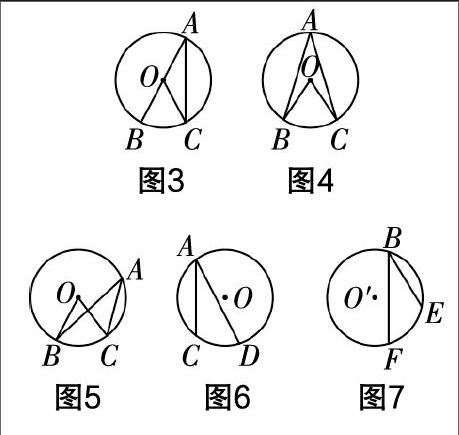
（小组合作、交流，分别汇报三种不同情况下圆周角∠BAC与圆心角∠BOC之间的关系，如图3、图4、图5）
（5）相等的弧所对的圆周角和圆心角也有这样的关系吗？如图6和图7，在等圆☉O和☉O′中，等弧所对的圆周角∠A与∠B相等吗？
（6）你能用自己的语言描述该数学结论吗？
总结归纳 同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半.
设计说明 探究活动分为2个层次，第一个层次让学生画出同弧所对的圆周角和圆心角，体会一条弧所对的圆周角有无数个，而圆心角只有一个，猜想同弧所对的圆周角相等. 第二个层次，考虑圆周角和圆心角之间的关系，先将圆周角按照与圆心的位置关系进行分类，让学生深刻感悟到分类的数学思想，分类后自然会从最特殊的情况出发，继而探究出其余两种一般的情况，突破本节课的难点.
4. 小结提升
（1）你是如何理解圆周角概念的？
（2）我们是如何探究出圆周角性质的？
（3）圆周角的性质有什么用处？
（4）通过研究圆周角，你积累了哪些学习的方法或经验？
设计说明 从知识方法、过程等方面进行课堂小结，鼓励学生从获取知识、形成技能、发展能力等方面谈自己的收获和体会，不仅能帮助学生整体上掌握所学的知识和方法，便于课后巩固，而且能使学生逐步体会一些重要的数学思想方法.
教学感悟
1. 引导学生经历数学概念的形成过程
教学概念时，教材上更多的是概念的直接呈现，教师需要站在思维发展的角度来钻研教材，力求展现概念的形成过程，让学生亲身经历、体验概念形成的过程，加深对概念的理解. 具体来说，可通过一些常用的步骤进行概念教学，让学生体验概念的形成过程.
（1）通过一组实例，抽象出共同的属性，给出新概念的定义. 本节课中，类比圆心角的概念，学生猜想出圆周角的顶点在圆上，并通过自己画图，体验角的两边可与圆都不相交，一边与圆相交，两边与圆相交，从所画图形中的圆周角抽象出共同属性，即角的顶点在圆上，且角的两边都与圆相交，从而给出圆周角的概念.
（2）深入挖掘新概念的内涵和外延，抓住本质. 圆周角的概念相对来说是具体的，学生在学习过程中会遇到更多抽象的概念，需要我们去深入挖掘，让学生不仅知其然，更知其所以然.
（3）建立新概念和已有认知结构中适当内容的联系，阐明概念之间的内在联系，形成概念系统，并且让学生尝试用自己的语言表述概念. 如将圆周角与圆心角相联系，类比学习.
（4）设计练习，从不同的角度灵活训练，甚至可以设置错误情境，引导学生运用已有的知识和经验去分析错误、尝试矫正，让学生在反思中加深对概念的理解. 如设置一组练习让学生判断哪些角是圆周角，从各个维度去考查，从而提炼出其必备的条件.
2. 引导学生经历数学规律形成的过程
重视学生数学学习的过程，让学生真正参与进去，经历观察、实验、猜想、验证、推理、反思、交流等过程，发现甚至创造出定理，才能促进学生完成知识的建构过程.
在设计数学活动时，要关注知识自身发展的轨迹. 如设计圆周角性质探究活动时，我们试着还原圆周角定理的发现过程，先发现同一条弧所对的圆周角有无数个，但所对圆心角只有一个，因此设计了先画角的活动. 再发现圆周角有无数个，但与圆心的位置关系只有三种，因此设计了观察圆周角，并从角的数量、大小、位置去思考. 再发现圆心角是唯一的，试着研究与圆周角的关系，从特殊情况入手很容易发现同一条弧所对的圆心角是圆周角的两倍，同弧所对的圆周角相等，这一问题便迎刃而解.
设计时还要关注知识之间的内在联系. 数学学习是建立在原有认知体系之上的，是对原有认知体系的不断扩展，只有所学新知识纳入原有的认知体系中，才能被学生真正理解、掌握和应用. 在研究圆周角的时候，考虑到学生已有知识经验和认知发展水平，已掌握圆心角的概念及相关性质，因此，在设计时采用类比学习法，能很自然地联想到圆周角与弧、圆周角和圆心角之间的关系.
3. 引导学生经历思想方法的提炼过程
数学思想方法是潜藏在数学知识深层的隐性知识，直接揭示显然不行，学生要经历解决数学问题的过程，亲身体验和具体操作，才能真正领悟. 教学设计时，要在概念、性质、法则、公式、定理等的形成过程中适时渗透，让学生掌握知识的同时，体验到深层的数学思想方法，使学生思维产生质的飞越.
具体来说，要通过设计一些有效的数学活动，引导学生主动参与结论的探索、发现过程，在解决问题的过程中对数学思想方法做深层次的思考. 如本节探究活动的设计中，学生在研究无数个圆周角的问题中，会去思考如何给这些角进行分类. 研究圆周角和圆心角时，会思考三种情况下先从哪种情况出发等，在创造性的思维活动中亲身体验.
关注学生的过程体验，我们要关注的不止这三个方面，还需要结合教学实践去不断摸索，不断优化教学设计，设置有效的数学活动，让学生操作、思考、交流，体验数学结果的形成过程. 另外，在课堂上，应给学生提供充分从事数学活动的时间和空间，让学生在活动中充分探索与发现，亲身体验与实践，真正参与到课堂中来.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 1:24:47