《一种灾害应急物资调度模型的单亲遗传算法求解》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

一种灾害应急物资调度模型的单亲遗传算法求解

范文

王清+陈海松+章瞻良

摘要：为在物资供应能力有限时解决需求点数量剧增给决策带来的困难，建立了灾害应急物资配送数学模型，改进了随机生成初始种群办法，采用了新的精英保留策略以加快最优策略的生成。仿真实验结果表明，改进的单亲遗传算法相对标准算法和随机解具有更高的目标值和更好的适应性，可较快获得可靠的分配方案，提高了应急救援的及时性与物资利用率。

关键词：灾害应急；物资配送；单亲遗传算法

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2017）14-0160-03

21世纪以来，各种人为、自然灾害造成大量人员伤亡与财产损失，为在灾害发生后的黄金时间内进行救援，须尽快做出应急物资的配送方案。但重大灾害的物资需求点较多，调度中实际需求与配送数量常有偏差，造成应急物资的局部堆积浪费。另外，考虑物资生产单位的供给能力限制，使物资配送决策变得更加复杂，必须找到合理有效的物资配送方案，提高物资利用率，以获取最大人群的救助。

针对灾害发生时的物资配送问题，学者做了大量研究。王玲玲考虑了时间约束，利用遗传算法求解了双目标配送方案。Li等重点研究了时间与成本最小下的应急物资调度，结合线性规划与粒子群进行求解。姜金贵-引基于粒子群算法，在多种约束条件下求得了最小物资成本的调度方法。何珊珊結合dijkastra与遗传算法，研究了应急物资的多阶段配送路径问题。栾盛磊以里程与时间为模型目标，使用遗传算法进行求解。

智能算法，如遗传算法面对染色体编码可重复问题，必须通过顺序交叉（Ox）、部分匹配交叉（PMX）、周期交叉（Cx）等复杂操作来获取可行解，耗时且效率低下；且重灾下需求点数量剧增时，原模型产生新解速度慢，实用性欠缺。基于此，结合具体的调度模型，利用单亲遗传算法无需交叉的优势，对其初始种群的生成办法进行重新设计，采用新的精英保留策略以改善解的多样性，使路径规划问题得以快速解决。

1模型建立

不同应急条件下物资配送策略有较大区别，为明确研究问题，考虑灾害实际情况，对模型作几点假设：1）被救助人员对固定种类物资的消耗速度不一样，为非线性关系；2）所有人员对物资的需求紧急度是一致的；3）物资生产供应能力是有限。

应急物资配送路径规划数学模型描述如下：

（1）式为目标函数，代表被救助人数总和最大。效益矩阵V中各需求点在不同物资补给量下的救助人数为事先给出。（2）式为供应点能力约束，显然，用完所有物资具有更大的目标值，故最佳配送方案中约束条件（2）必取到等式，（3）式为整数约束。

2单亲遗传算法的问题求解

单亲遗传算法（Partheno-Genetic Algorhhm，PGA）取消了遗传算法中的交叉算子，所有变异过程均在一条染色体上进行，避免了由于交叉产生大量不可行解，提高了新解的产生效率，且能和其它算法有效结合。李茂军等证明了PGA的基因重组隐含交叉算子，其子代仍能保留父代个体的大部分遗传特征。PGA基本过程主要包括编码与适应度计算、选择、变异、精英保留、结果输出等步骤。针对标准单亲遗传算法中初始种群产生随机性强与精英保留策略效率低的不足，算法进行了相应改进，以提高求解速度与精度。

2.1编码策略及适应度函数

在编码策略选择时，采用实数编码直观简单，本模型采用此方法。由于每个需求点的资源供应量si为不大于m的离散值，则模型解转变为n个离散取值的组合优化，将一个组合视为单独个体。在没有物资总量限制的情况下，这样的编码串共有（m+1）n个。

为方便计算，适应度函数直接取目标函数。

2.2初始种群产生方法改进

随机生成的办法在需求点数量较多时效率极低，利用PGA不要求初始种群具有广泛多样性的优点，本文初始种群拟产生采取以下改进办法。

（1）最大化平均分配。将m平均分配到所有需求点n，得到初始解s1=[m/n]（[*]表示向下取整，下同）；

（2）分配剩余物资量。经最大化平均分配后，剩余的物资量L=m-[m/n]·n

（3）随机扰动。随机产生一个整数值{u|u∈[1，[m/n]-1]，u为整数}，两次选择个体的任意p（1≤p≤n）个需求量，分别对（2）中初始解进行加u和减u操作；

（4）重复1-3，得到满足初始数量要求的种群。

2.3遗传操作

单亲遗传算法剔除了标准遗传算法中的交叉过程，其它算子与遗传算法基本一致。主要包括选择、变异与换位。

（1）选择

PGA与标准遗传算法的选择算子类似，这里采用赌轮盘的选择概率。

（2）随机变异

在所有个体中，适应度函数值越大的个体被完整继承的概率越大，也就是说其变异概率越小，取变异概率Q（i）=1-P（i）。在进行变异时，由于约束条件的存在，采用以下变异规则：随机取某个体T中两个需求量ti、ti比较大小，记为max与min，产生一个c∈[1，max-min-1]的随机数，若max-min-1≤1，重新选择，变异结果的两个需求量为（max-c）和（min+c），如此变异得到第2个子代群体sp2。随机变异的含义是将某个需求点的部分物资调运给另一个需求点。

（3）基因换位

本文采用单点换位，在某一个体的基因位上随机将其两个不同位置进行交换，换位概率采用选择算子的概率算法。换位变异的含义是指将任意两个需求点的物资供应量进行了调换。

（4）基因倒位

基因倒位算子是在一定的概率下，将个体的部分基因首尾倒置的过程，进行倒位的子串及长度是随机选择的，本模型将所有基因倒位。倒位的意义在于按照一定概率，将某个个体，将第一个与最后一个需求量对调，第二个与倒数第二个需求量对调……依次进行。

（5）基因移位

本模型中的移位是以一定概率，选择某个个体中的基因子串，将其前移或后移到某位置，重新生成新的个体。移位的物理意义在于将某些连续物资量替换为其他需求点的物资量，其后的所有需求点物资均发生顺移改变。

2.4精英保留策略的改进

在遗传的迭代过程中引入最优保持策略是必要的，也是全局收敛的前提。为提高算法收敛速度与结果精度，本文采用如下精英保留策略：

（1）将初始的w个个体作为历史最佳种群bestPop，适应度最佳个体f1作为历史最佳个体gBest；

（2）从五种遗传操作子代组成的种群挑选适应度最好的前w个作为初选种群newPop，记初选种群中最大和最小适应度为f2max、f2min自，对应个体为maxPop，minPop；

（3）比较历史最佳个体与初选种群的适应度值：

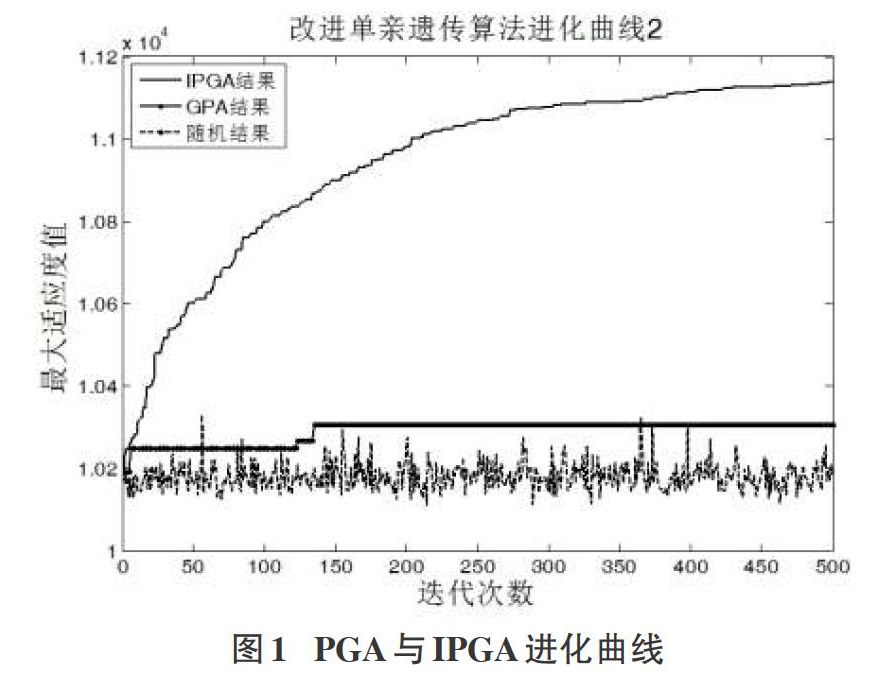
a）若f1

b）若f2min≤f1≤f2max，将newPop中的minPop替换为gBest作为新的最佳种群，maxPop替换gBest，进行下一步迭代；

c）若f1>f2max，bestPop，gBest不变进行下一次迭代。

该种精英保留策略在利用了五种遗传算子并行生成的种群中所有精英个体以外，尽可能多的保留了优于历史最佳个体的所有新的个体，使最佳种群更新速度加快。对于初始种群多样性不够的本模型，可较大提高解的搜索效率。

3实验仿真与分析

根据近二十年的突发灾害来看，地震、海啸涉及面广、破坏性强，物资配送范围极大，需求点数量与物资供应量劇增。考虑物资需求点数量n=60，供应能力限制为m=2000，分别用PGA、IPGA进行仿真实验，将各解与随机结果对比。

基本参数设置为：初始种群规模w=50，倒位变异概率为0.8，移位变异概率为0.7，迭代次数500。实验结果如下：

结果分析：从运算结果中可以看到，PGA算法得出的最优解为10344，相对随机均值提高了1.4%，个别随机值甚至大于该解；IPGA求得的最优解为11134，相对于随机最大值提高了9.26%，相对PGA提高7.63%，说明改进后的单亲遗传算法在求解质量上更好，并且可以看出，算法到了500次迭代仍然没有处于稳定（经实验，在约3000次迭代后将达到稳定值），故时间要求宽松时，运行更多的迭代次数将进一步改善获得的最优解。此时常用的枚举法由于需求点n过大计算量剧增，而动态规划法阶段太多，分析难度大，已不适合求解。

4结束语

为解决在灾害应急物资调度路径规划中，由于需求点数量剧增与总量约束导致原组合优化求解困难的问题，构建了灾害应急物资配送调度路径规划仿真模型，基于单亲遗传算法特性，对其中初始种群产生办法与精英保留策略进行了改进，避免了大量不行解的产生，保证了算法的运算速度，并通过模拟仿真验证了改进算法的可行性与优越性。模型一定程度缓解了灾害应急物资调度时间紧、需求点多、规划困难的现状，能利用有限物资覆盖最大人群，具有明显的经济和社会价值。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。