《PSO-BP神经网络预测模型在智慧课堂中的应用研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

PSO-BP神经网络预测模型在智慧课堂中的应用研究

范文

郭涛魏勇熊杰

摘? 要：大学生的学习成绩与其学习状态和习惯有正相关性。教师工作手册中记录的考勤、答问与作业信息反映了学生的学习状态，智慧课堂中的随堂提问、课后作业、座位偏好等信息进一步反应出学生的行为习惯。充分利用上述数据进行期末成绩预测并向学生反馈学业警示和鼓励信息，将对教学起到积极作用。设计了PSO-BP神经网络预测模型来进行学生行为数据挖掘，筛选了具有代表性的数据作为神经网络的输入，选择课程成绩作为神经网络的输出，成绩预测误差为12%，为提高教学质量提供了新的思路。

关键词： PSO算法; BP算法; 神经网络; 成绩预测; 智慧课堂; 数据挖掘

中图分类号：G642;TP183? ? ? ? ? 文献标识码：A? ? ?文章编号：1006-8228（2021）03-52-05

Research on the application of PSO-BP neural network predictive model in smart classroom

Guo Tao1， Wei Yong1， Xiong Jie2

（1. Electronics & Information School， Yangtze University， Jingzhou， Hubei 434023， China; 2. Huanggang Normal College）

Abstract： College students' academic performance is positively correlated with their learning status and habits. The attendance， Q&A， and homework information recorded in the teacher's work manual reflects the student's learning status. In the smart classroom， information such as in-class questions， homework， seat preference， etc. further reflects the behavior of students. Making full use of the above-mentioned data to predict the final grade and feedback the academic warnings and encouraging information to students will play a positive role in teaching. The PSO-BP neural network prediction model is designed to conduct student behavior data mining， representative data is selected as the input of the neural network， and the course score is selected as the output of the neural network， and the score prediction error is 12%， which provides a new idea for improving the teaching quality.

Key words： PSO algorithm; BP algorithm; neural network; performance prediction; smart classroom; data mining

0 引言

2017年7月，國务院印发了《新一代人工智能发展规划》[1]，首次提出要利用智能技术实现教学方法的改革，构建新型的智能教育体系。2018年10月，教育部发布的“教高 40条”[2]中明确指出要大力推动人工智能（AI）等技术在教学与管理中的应用，打造适应学生需求的智慧课堂，推进现代信息技术与教育教学深度融合。由此可见，人工智能技术方法将是实现智慧课堂和推动教育教学改革的核心技术方法。

目前，国内高校纷纷探索将大数据、人工智能等前沿技术应用于智慧课堂中。例如：文献[3]探索构建教、学、考、评的闭环教学模式，线上与线下相互结合，为打造智慧课堂提供了合理的方法和完备的路径。文献[4]针对学生课堂学习过程中学习效果的量化和教学过程数据化困难的问题，提出基于微信公众号的AI技术融合方案，如使用大数据挖掘技术来量化学习效果等方案，实现“AI+教育”的智慧课堂。

基于以上背景，借助于智慧课堂教学软件，使用多种人工智能技术对学生学习过程中的数据进行量化（如通过图像识别技术实现课堂考勤、抬头率检测和表情识别等）。量化后的学情数据结合神经网络技术进行教育大数据的挖掘，从大量的教育数据中分析学生的学习效果，并给出成绩预测。以预测结果为依据，采取不同的干预措施，这样不仅可以为教师设计与调整教学方法提供理论依据，还可以为提高学生的课程考试成绩以及提升高校的教学质量提供帮助和支持，进一步促进教育体制的改革、发展和完善[5-6]。因此，开展智慧课堂结合神经网络预测模型的应用研究具有理论指导意义和实际应用价值。

1 智慧课堂教学

1.1 教学过程

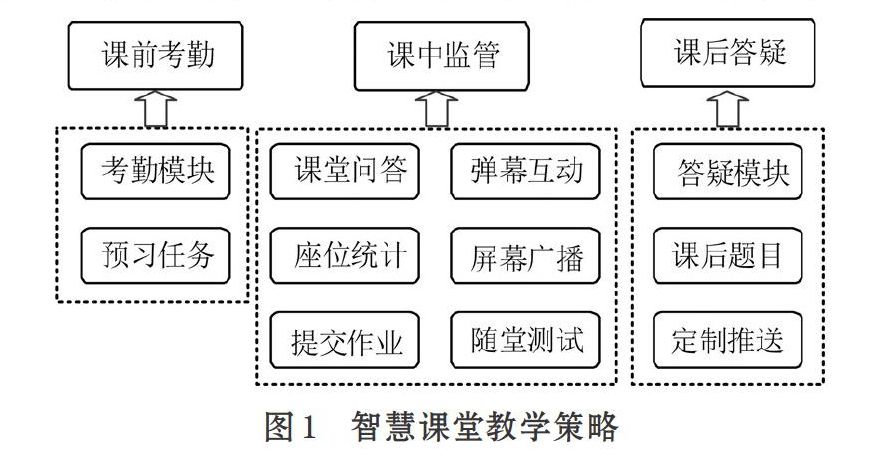
智慧课堂的教学过程分为课前考勤、课中监管和课后答疑三个阶段。课前考勤是教师对学生平时成绩打分的重要依据，智慧课堂依托物联网设备进行人脸识别打卡，有效地避免了时间和人力成本的浪费、提升效率、考勤全面。课中监管的过程中，智慧课堂软件可以实现课堂问答，弹幕互动，座位信息识别，教师端屏幕广播，学生端提交作业，随堂测试等功能。例如：针对部分同学精力不集中问题可以进行课堂点名问答;对于部分实践性较强的内容教师可以将自己的屏幕广播给同学们进行观看学习。在课程结束后，教师可以解答同学们的问题、根据每个同学的学习情况推送个性化的学习内容、布置课后作业来巩固知识。

1.2 智慧课堂与成绩预测

随着“腾讯课堂”、“雨课堂”等优质线上智慧教育平台在大学教学过程中的广泛应用，极大地促进了智慧课堂从理念到现实的应用转换。然而在实际应用过程中，虽然此类平台详实记录了大量教学过程数据和信息，但这些数据却只形成了单项排序和统计图表[7]，数据之间相互独立，没有发挥智慧课堂的全部优势。文献[8]以《高等数学》课程为例，运用SPSS软件对学生的期末成绩进行统计分析，结果表明，学生平时表现和期末考试成绩之间的相关系数为0.785，说明学生的平时表现和课程考试成绩的相关度很高。由此可见，使用智慧课堂记录的大量学生的历史表现数据对学生未来的课程成绩进行预测是可行、可信的。如果我们针对不同预测成绩，采取对应的学业预警或学业鼓励方法，将对于改善学生的课堂表现，减少挂科率具有积极的意义。

图2为针对不同预测成绩的应对策略，其基本思想是：对于预测成绩低于60分的同学，及时地发出学业预警电子邮件，警示该同学改变现状，避免出现该门课程不及格的结果;如果发出预警后该同学仍无动于衷，这将导致后续预测成绩仍然不及格，此时可以通过邮件或电话方式通知该同学的辅导员或家长，进行早期干预、使用多种手段来督促该生学习;而对于预测成绩高于85分的同学，可发送学业鼓励邮件，鼓励其再接再厉，继续保持当前状态将会取得理想的分数。

1.3 成绩预测模型

BP神经网絡具有很强的非线性拟合能力，可映射任意复杂的非线性关系，而且学习规则简单，便于计算机实现，具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力，因此在数值拟合预测方面得到了广泛应用。文献[9]筛选出影响学生表现的因素作为神经网络的输入数据，使用往届学生的历史成绩作为输出结果，基于BP算法建立了人工神经网络预测模型，预测学生表现的测试精度达到了84.6%，说明了BP神经网络在预测学生成绩方面具有很好的鲁棒性，验证了此方法对解决成绩预测问题的可行性。

使用BP神经网络需要首先确定网络的输入和输出，而智慧课堂软件会采集课程管理过程中的各类数据，这包括考勤数据、问答统计、互动次数、测试分数、作业分数、座位信息等数据，究竟选取哪些数据作为神经网络的输入显得尤为重要。文献[10]使用聚类算法对影响学生成绩的因素进行分析，结果表明在影响学生成绩的主观因素方面，学生的课程兴趣、课前考勤、课堂状态、课后作业对成绩影响因素较大。综上，选取学生的课前考勤、课堂表现、课后作业三类信息作为神经网络的输入;成绩预测模型的输出为一个节点，即该课程的综合成绩。

2 PSO-BP神经网络拓扑

2.1 BP神经网络

BP神经网络是一种采用误差反向传播算法并不断进行修正训练的一种多层前馈式神经网络，是目前应用最为广泛的人工神经网络模型之一，广泛应用于网络检测、信息预测等领域中[11]。其基本思想是利用LMS学习算法，在神经网络的训练过程中利用损失函数和不同的优化器来更新权值、阈值，从而最小化神经网络的输出值与实际值之间的偏差。典型的神经网络拓扑结构包含输入层（Input）、隐含层（Hidden）、输出层（Output）的3层网络结构。

图3中Ii，Hj，Ok分别为输入层、隐含层、输出层的某一单元，从输入层单元Ii到隐含层单元Hj的连接权值为wij，阈值表示为a，从隐含层单元Hj到输出单元Ok的连接权值为wjk，阈值表示为b。其学习过程包括前向传播过程和依据输出值和期望值的偏差进行反向传播更新权值阈值两部分。

⑴ 前向传播计算

第j个隐层神经元的输出为：

[Hj=? s（i=1iIiωij+bj）]? ⑴

第k个输出层单元的输出为：

[Ok=s（k=1kHjωij+bk）][ Ok=s（k=1kHJ·wjk.+bk）]? ⑵

⑵ 反向传播更新

神经网络正向传播输出为：

[Ok=（O1，O2，O3，…，Ok）] ⑶

则神经网络在（Ii，Ok）的MSE损失函数为：

[Ek= 12kk=1k（Ok- Ok）2]? ⑷

为减小输出误差，权值的修正从输出层开始向前一层进行修正，根据提前设定的学习率α，得到权值调整值为：

[?ωjk= -α?E?ωjk]? ⑸

然后修正权值为：

[ω=ω+?ω=ωjk-α?E?ωjk]? ⑹

至此，完成一次BP算法的训练过程。但由于BP神经网络中的参数众多，每次训练过程都会更新大量的权值和阈值，计算量也会随着层数和节点数的增加呈几何倍增加，容易产生收敛速度变慢的问题。同时BP神经网络在训练过程中，其修正值容易陷入局部最优解，从表面看误差值符合要求，但此时得到的解却不一定最优。

2.2 PSO算法优化BP神经网络

考虑成绩影响因素的非线性特征，以及对其影响因素的复杂性，同时为了克服BP神经网络容易陷入局部最优的缺陷，加快BP神经网络的收敛速度，本文采用粒子群优化算法（PSO算法）来优化BP神经网络的初始参数。PSO算法会在更大的空间内搜索最优解，具有很强的全局寻优能力，一定程度上弥补了BP神经网络易陷入局部最优的不足，能进一步减小神经网络输出误差。PSO-BP优化算法的具体流程如下：

Step1 确定BP神经网络的拓扑结构，对于BP神经网络隐含层数的选择，在满足精度要求的情况下选取一个隐含层可以避免层数过多导致的过拟合问题。因此实验选择典型3层BP神经网络结构。隐含层节点数的选择有如下公式：

[hidden=input+output+a] ⑺

当确定了输入节点数为3，输出节点数为1时，调节常数a的取值范围是1-10，因此最优隐含层节点数范围确定为3-12之间。最后通过反复实验对比不同隐含层节点数的神经网络性能表现，确定隐含层最优节点数为4，最终的BP神经网络拓扑结构如图4所示。

Step2 初始化种群，将BP神经网络各层的连接权值wij、wjk和阈值a、b拼接成为单个粒子的位置向量。如图3中的权值阈值可拼接得到单个粒子的位置向量：

posn=（w11，w11， a11， b11…wij ，wjk ，aij，bij）=（posn1 …posnd）

再初始化每个粒子对应的速度向量：

vn? = （vn1…vnd）

在迭代搜索的过程中记录第i次更新得到的个体粒子最优位置记录为：

pbestn? = （pn1…pnd）

记录当前群体最优值为：

gbestn = （pg1…pgd）

Step3 使用粒子群优化算法的迭代公式进行迭代寻优

[vi= ω*vi+c1*rand*pbesti-xi]

[? ? ? ? ? ? ? ? ?+c2*rand*gbesti-xi]? ? ⑻

采用迭代公式运算时，式8中的c1和c2分别代表个体学习率和群体经验的学习率。其中，惯性因子w较大时可获得较强的全局寻优能力，随着迭代次数的增加，迭代的全局收益逐步降低，此时逐渐减小惯性因子w可以进行精细的局部搜索，这种方法称为线性递减权值策略，可以获得更好的全局寻优结果。

Step4 粒子的适应度函数同样使用均方差损失函数进行评估当迭代次数达到设置的上限或适应度函数满足设置的精度要求，则停止迭代，完成优化权值阈值的初值。

Step5 优化后进行训练，此时BP神经网络获得了最优的权值、阈值，在此基础上开始训练神经网络，直至满足设定的最小误差精度，則停止训练，输出结果。

3 实验与分析

3.1 数据处理和参数设置

实验中所有的学生数据来源于多名教师教学工作手册中的学生考勤与成绩记载信息和智慧课堂软件记录的数据库，如图5所示。主要获取以下三种信息：①课程教学的考勤信息（人工签到和软件统计签到数据）;②课堂上学生回答问题情况的统计信息（人工记录和结合软件记录）;③学生的作业完成情况统计信息（人工打分和软件统计数据）。收集到的信息经过数据筛选和清洗后，进行统一量化，建立百分制的样本数据集，如表1所示。

预测模型的初始化参数设置原则如下：加速因子c1=1.5，c2=1.5，初始权值采用线性权值递减策略，wmax=0.9，wmin=0.4，种群规模N=200，最大迭代次数设置为500。实验使用相同的网络结构和初始化参数来训练BP神经网络和PSO-BP 神经网络并进行预测输出。

3.2 实验结果与分析

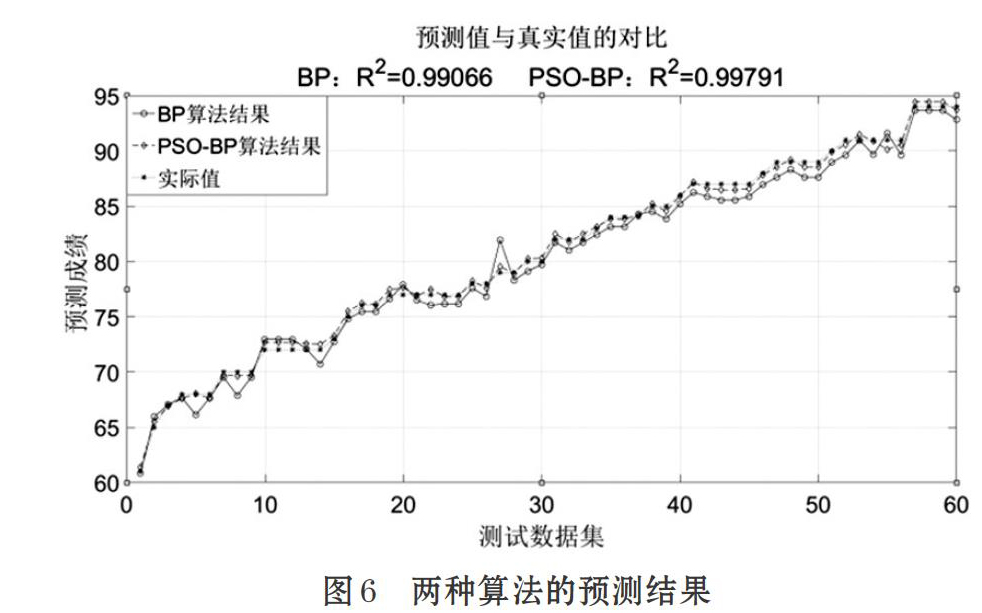
使用PSO算法在优化BP神经网络的权值、阈值时，其适应度函数的输出值随着粒子寻优的迭代更新，在模型训练完成后，导入60个测试数据集对模型进行测试。为了便于显示，60个测试数据集按照实际的课程成绩升序排序。最终得到传统BP神经网络和PSO-BP网络的输出，对比结果如图6所示。

从图6可以直观地看出，BP算法和PSO-BP算法均能较好的逼近非线性的实际课程成绩。但PSO-BP算法结果的决定系数R2，要大于BP算法的结果，因此PSO-BP算法的非线性拟合效果要优于传统BP算法的结果。

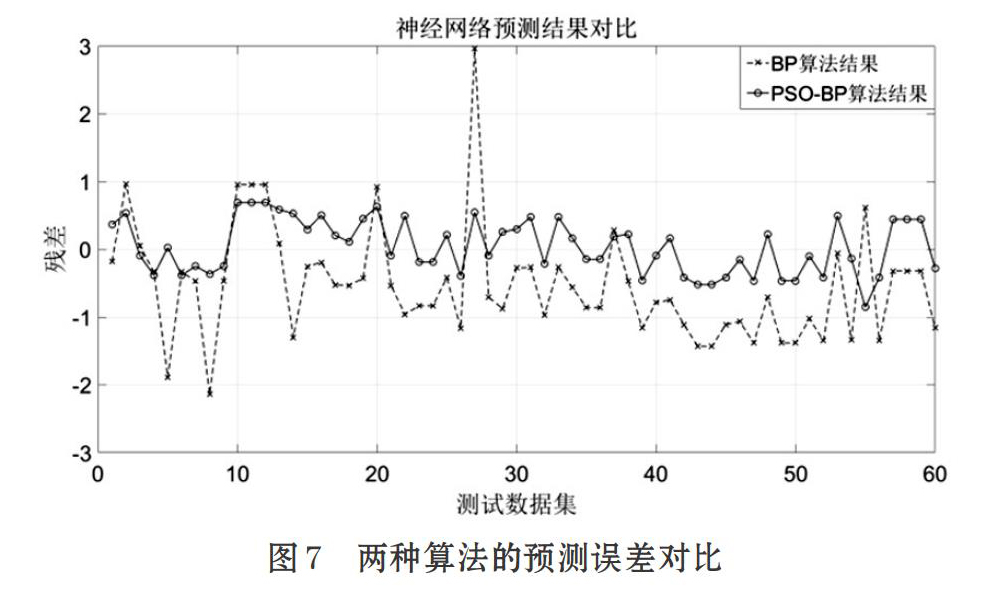
图7进一步给出了PSO-BP和BP算法的预测误差对比结果。其中虚线曲线代表BP算法输出结果，误差范围在[-2.2，3]以内。实线曲线为PSO-BP算法结果，误差范围是[0.8，-0.8]，对比误差范围可见，PSO-BP较于传统BP算法明显较优。

综上所述，PSO-BP算法和BP算法均能获得较好的预测结果，前者的全局寻优能力优于后者，有效提高了预测精度（多次测试均在±3%内），对各层次水平的学生均能达到较高的预测精度。

4 结束语

本文提出了一种应用于智慧课堂的基于神经网络的成绩预测模型，该模型可利用教师的教学工作手册或者智慧课堂软件记录的学生课堂表现信息进行教育数据挖掘，能获得较好地预测学生的期末成绩，其预测精度达到±3%。若希望进一步提高预测精度，可考虑在网络的训练过程加入影响考试成绩较强的因素，例如学生的座位偏好信息，将可以进一步提高预测结果的准确度，当然这也对智慧课堂软件提出了更高的要求。

充分利用神经网络预测模型，有针对性地使用多种方法来激励学生的学习状态朝着积极的方向发展，不仅可以为制定下一步的教学策略提供帮助，还能让高校的教育教学工作和教育管理工作更有成效[12]。在人工智能技术不断发展的今天，智慧课堂结合人工智能技术的应用前景是无可估量的，二者的深度融合也是未来教育发展的必然趋势。

参考文献（References）：

[1] 中华人民共和国国务院.国务院关于印发新一代人工智能发展规划的通知 [EB/OL].（国发〔2017〕35号）.

[2] 中华人民共和国教育部.教育全面提高人才培养能力的意见 [EB/OL].（教高〔2018〕2号）（简称“教高40 条”）.

[3] 曲双红，孟令显.借助雨课堂，创新构建“教、学、考、评”闭环教学模式[J].教育现代化，2019.6（85）：268-271，278

[4] 李群，徐鼎，肖甫.基于微信公众号的“AI+教育”智慧课堂实施方法[J].计算机教育，2019.2：136-139

[5] 陈佳明，骆力明，宋洁.大学基础课课程成绩加权投票预测模型研究[J].现代电子技术，2020.43（1）：93-98

[6] 彭涛，丁凌云.基于教育数据挖掘学生表现预测模型构建研究[J].黑龙江高教研究，2015.11：55-58

[7] 杨世瀚，章维亚.基于“雨课堂”的教学过程知识库构建及学生成绩智能评估[J].高教学刊，2020.14：15-18

[8] 董倩倩.基于spss的《高等数学》期末考试成绩评价与预测[J].教育现代化，2019.6（85）：236-237，246

[9] Samy Abu Naser， Ihab Zaqout. Predicting Student

Performance Using Artificial Neural Network： in the Faculty of Engineering and Information Technology.[C]. International Journal of Hybrid Information Technology，2015.8（2）：221-228

[10] 谢娟英，张宜，陈恩红.学生成绩关键因素挖掘与成绩预测[J].南京信息工程大学学报（自然科学版），2019.11（3）：316-325

[11] Samy Abu Naser， Ihab Zaqout. Predicting Student

Performance Using Artificial Neural Network： in the Faculty of Engineering and Information Technology，2015.8（2）：221-228

[12] 胡祖辉，徐毅.大数据背景下高校教育数据的分析与应用研究[J].现代教育科学，2017.1：109-11

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。