网站首页  词典首页

请输入您要查询的论文：

　

标题 基于随机下采样和SVR的蛋白质?ATP绑定位点预测
范文 余健浩+孙廷凯



摘 要： 将蛋白质序列的ATP绑定位点与非绑定位点进行分类是个不平衡的二分类问题，其中绑定位点是样本数目稀少的正类样本，非绑定位点是样本数目众多的负类样本。根据机器学习关于可以将分类问题作为回归问题的特例的观点出发，并根据所研究问题本身的特点，在此提出一种基于随机下采样和支持向量回归的蛋白质?ATP绑定位点预测方法。首先，使用滑动窗口抽取蛋白质序列中每个残基的特征，得到一批不平衡的两类样本；其次，应用随机下采样策略，消除正负样本存在的显著不平衡；最后，使用支持向量回归建立预测模型，并选取合适的阈值进行蛋白质?ATP绑定位点的预测。在标准数据集上的实验结果以及与几种最新报道的预测方法的对比结果，验证了本文所述方法的有效性。
关键词： 蛋白质?ATP绑定位点； 位置特异性得分矩阵； 滑动窗口； 支持向量回归模型； 随机下采样
中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）04?0019?06
0 引 言
三磷酸腺苷（Adenosine 5′?triphosphate，ATP）在分子细胞生物学中扮演着一个重要的角色，如膜运输、细胞活性、肌肉收缩、信号、复制和转录DNA、以及各种代谢过程[1?2]。ATP与蛋白质相互作用是通过蛋白质的ATP绑定位点进行ATP绑定，通过蛋白质?ATP水解提供化学能，利用这种化学能提供动力，蛋白质才能够执行多种生物功能。显然，ATP需要和蛋白质残基（即氨基酸，一维结构上即为蛋白质序列中的若干位点）绑定才能在细胞活动中完成各种任务，因此研究预测蛋白质残基的ATP绑定位点对于人体蛋白质的功能分析显得尤为重要。此外，蛋白质?ATP绑定位点的准确定位也在化疗药物的研发设计[2]中表现出比较突出的价值。因此，准确地定位蛋白质?ATP绑定残基对于人体蛋白质的功能分析和药物设计都具有非常重要的意义。
目前确定蛋白质?ATP作用绑定残基的研究已经取得了很大的进展，然而，随着蛋白质测序技术的飞速发展，已经积累了大量的蛋白质序列数据未标定，传统的生物学实验方法往往遇到实验密集、昂贵、耗时等问题，因此从蛋白质序列出发通过智能计算方法[3] 预测蛋白质?ATP绑定位点有着迫切的需求。
Nobeli等人最初研究了在鸟嘌呤和腺嘌呤与蛋白质区别的分子识别方法，开创了用分子识别方法进行鸟嘌呤和腺嘌呤与蛋白质区别的先河，但是实验结果并不十分理想[4]。ATPint是最早被提出的专门用于蛋白质?ATP绑定残基的预测方法[5]。ATPint使用蛋白质序列的位置特异性得分矩阵（Position Specific Scoring Matrix，PSSM）作为基本的特征源。最近，Kurgan等人开发了两个更加准确的预测方法分别为ATPsite[6]和NsitePred[7]。其中，ATPsite主要基于序列、进化信息和二级结构的组合方法识别蛋白质?ATP绑定残基，而NsitePred可以对多种类型的核苷酸进行预测，如二磷酸腺苷（Adenosine diphosphate，ADP）、腺嘌呤核糖核苷酸（Adenosine monophosphate，AMP）等。以上两种方法均使用的数据为227个非冗余的ATP绑定蛋白质，其较大的数据量有利于较好结果的预测。
从机器学习角度看，蛋白质?ATP绑定位点预测是一个典型的不平衡学习问题[8]。不同类别样本的数量很明显不同，比如，ATP227数据，非绑定残基的数量是绑定残基的数量的23倍多。不同类别的样本在不平衡的情况下，直接采用传统的机器学习算法，即使得到了较高的识别率，但对于样本数目较少的正类来说，分类效果则未必好。解决不平衡学习的基本方案是改变样本在不同类别的分布，调整样本分布[9]。而随机下采样是比较常用的调整策略，其做法是从众多的负类样本中随机选取一部分，使正负样本达到平衡，在此基础上执行传统的机器学习算法，提高系统的学习效果[10]。
本文研究了蛋白质?ATP绑定位点预测问题，根据机器学习关于可以将分类问题作为回归问题的特例的观点出发，并根据所研究问题本身的特点，提出了一种基于随机下采样和支持向量回归的蛋白质?ATP绑定位点预测方法。在标准数据集上的实验结果以及与几种最新发布的预测方法的对比结果，验证了本文所提出方法的有效性。
1 数据集
本文所采用的数据集来自Chen等提供的227条非冗余的蛋白质序列（简称ATP227）[6]，其中包含3 393个ATP绑定残基，80 409个非绑定残基。从两个类别样本的数据数量中明显可以看出蛋白质?ATP绑定位点预测是一个典型的类别不平衡问题。从相似度角度看，ATP227中任意两条蛋白质序列的相似度低于40%。为了验证本文所述方法的泛化能力，使用了一个包含17条蛋白质序列的独立测试集[7]。该独立测试集中任意两条序列的相似性低于40%，并且独立测试集中任一序列与ATP227中的任一序列的相似性也低于40%。
2 提出的方法
2.1 方法原理与思想
蛋白质?ATP绑定位点预测问题就是要分清蛋白质序列中，哪些位点的残基是绑定的，哪些是非绑定的，这是个典型的不平衡二分类问题，其中绑定位点是样本数目稀少的正类样本，也是最感兴趣的类别，而非绑定位点是样本数目庞大的负类样本。
按照机器学习的观点，可以将分类问题和回归问题统一起来考虑[11?12]。假设给定一批样本[（xi，yi）]，i=1，2，…，n，其中样本点[xi∈Rd]，对于回归问题，[yi∈R]，对于分类的问题，这里[yi]为离散的类别标号。一方面，把回归问题转换为分类问题，相当于将每个[yi]分别加减一个回归误差允许阈值[ε]，从而得到第一类样本[（xi，yi+ε）]和第二类样本[（xi，yi-ε）]，找到的回归曲线尽可能地穿过所有原始样本点，相当于把这两类样本正确分开，原始的回归问题于是转化为分类问题[11]，这种情况是平衡的两类分类问题。另一方面，分类问题相当于将高维样本数据[xi∈Rd]向离散的类标号[yi]=1，2，…，c（而不是连续的实数）做映射，因此可以将分类看作是回归的特例，这种情况各类样本不一定是平衡的，二分类问题也不例外。但是不平衡会影响回归的精度，举个极端情况来说，比如正类只有一个样本，而负类有很多样本。既然回归问题的几何解释是回归曲线尽可能靠近所有样本点，使得总误差尽可能小，在这种情况下，回归曲线必然靠近占优的负类样本。因为这种情况下，无论正类样本还是负类样本，每个样本点对于回归问题具有同等意义的权重，或者说，少数的正类样本并没受到足够的重视。因此，有必要采取措施，使得正负样本变得均衡。
在蛋白质?ATP绑定位点预测问题中，每个残基属于绑定位点还是非绑定位点，不仅仅取决于残基自身是哪种类型的残基，更在很大程度上取决于附近的残基（即上下结构环境）类型及他们是否是绑定位点，换言之，是否属于绑定残基并非是一个0?1二值逻辑，而是有一定的置信水平的。因此，采用支持向量回归（Support Vector Regression，SVR）的方法，预测某个残基属于绑定残基的置信水平，更接近于问题本身的性质特点，然后选取合适的阈值进行判别，是一个比较合理的方法。基于这种考虑，提出并设计了一个基于支持向量回归的蛋白质?ATP绑定位点预测方法。首先对样本进行适当的平衡化处理，在此基础上，根据上文关于分类和回归问题关系的分析讨论，通过支持向量回归的方法构建模型进行预测。尽管支持向量机（Support Vector Machine，SVM）分类方法（support vector classification，SVC）已被广泛用于蛋白质?ATP绑定预测[13?14]。目前将支持向量回归方法用于蛋白质?ATP绑定预测问题的研究还较少，鲜有这方面的报道。基于以上分析，从蛋白质的序列出发，基于序列的位置特异性得分矩阵，使用滑动窗口抽取序列中每个残基的辨别特征；应用随机下采样策略，消除正负样本存在的显著不平衡；最后，使用支持向量回归模型进行蛋白质?ATP绑定位点的预测，选取最优阈值判别蛋白质?ATP是否绑定，得到预测结果。本文方法流程见图1。
2.2 特征提取与标准化
2.2.1 位置特异性得分矩阵
位置特异性得分矩阵（Position Specific Scoring Matrix，PSSM）能够在一定程度上反映蛋白质序列的进化信息，已经被其他研究者广泛用于生物信息学预测问题中，如蛋白质二级结构预测[13]、蛋白质?ATP绑定位点预测[14?19]、蛋白质功能预测[20]、横跨膜的螺旋线预测[21]、亚细胞定位[22?23]等。对于一个包含n个氨基酸残基的蛋白质序列，使用PSI?BLAST[24]（默认阈值E?value= 0.001）生成n×20的PSSM矩阵。
2.2.2 逻辑斯蒂位置特异性得分矩阵
对PSSM矩阵的每个元素是通过逻辑斯蒂函数进行标准化（称LPSSM）的。逻辑斯蒂函数定义如下：[f（x）=11+e-x] （1）
式中x是PSSM矩阵中原始得分。
2.3 随机下采样和支持向量回归
2.3.1 随机下采样
通常情况下，在一个不平衡的数据集中，采样方法可以使数据集平衡，从而能从不平衡的数据集中得到学习[25?27]。对于大多数的不平衡数据集，下采样方法可以提供一个较小的训练集，大量缩短训练和预测的时间，并且能提高分类精确度。随机下采样方法为从小类样本中无重复地随机抽取[Smin]个样本[N]次，即数据集较小的绑定位点为正样本，从大类样本中无重复地随机抽取[Smax]个样本[N]次，即数据集较大的非绑定位点为负样本，每次随机抽取后正样本和负样本的数量相同，即[Smin=Smax]，从而得到平衡样本集[S=Smin+Smax]。
2.3.2 支持向量回归
本文采用支持向量回归方法构建模型，使用广为采用的工具Libsvm[28]，在构建模型时，由于潜在的回归模型未必是线性的（实际研究中发现往往是非线性回归模型），为了建立非线性回归模型，先通过某个核函数诱导的非线性映射[Φ：x?Φ（x）]把原始数据非线性映射到特征空间中，在特征空间建立线性SVR模型。在实验中，将核函数类型采用径向基函数（Radial Basis Function， RBF）形式，如式（2）所示：
[K（x，xi）=exp（-x-xi2γ2）] （2）
式中[γ]为核参数。假定一个训练样本集[{x，y}n1]，训练输入参数[xi∈Rn]和输出预测值[y∈R]，SVR预测如式（3）所示：
[f（x）=i=1N（qi-q*i）K（x，xi）+b] （3）
式中：
[i=1N（qi-q*i）=0，0≤qi， q*i≤C，i=1，2，…，N] （4）
式中：[qi]，[q*i]为对偶参数且满足式（4）条件；[K（x，xi）]为核函数。
2.4 算法评价指标
几个经常使用的评价指标，即特异性（Spe）、灵敏度（Sen）、准确性（Acc）、马氏相关系数（MCC）。方法定义如下式：
[Spe=TNTN+FP] （5）
[Sen=TPTP+FN] （6）
[Acc=TP+TNTP+TN+FP+FN] （7）
[MCC=TP?TN-FP?FN（TP+FP）?（TP+FN）?（TN+FP）?（TN+FN）] （8）
式中：TP、FP、TN和FN分别代表正类预测为正类样本的个数、负类预测为正类样本的个数、负类预测为负类样本的个数和正类预测为负类样本的个数。预测的效果可以通过混淆矩阵[29]来表示，如图2所示。
在不平衡样本下，这些指标将用于选取最优阈值，并将在下文的实验结果中报告展示。
由于SVR的预测输出参数y是连续实数，而不是离散的类标号（例如在两类问题中，两类样本的类标号可分别标记为+1和-1），需要进行参数转化，选取合适的阈值，将SVR模型输出的连续实数y离散化为相应的类标号。从某种意义上说，SVR模型输出的连续实数y相当于分类器的置信水平，这也正是本文采用SVR回归模型进行蛋白质?ATP绑定预测的原因之一。通过逐步调整分类阈值，产生一系列的混淆矩阵。从每一个混淆矩阵计算对应的Spe、Sen、Acc和MCC指标参数，即四个评价指标对阈值是依赖的，它们随阈值的变化而变化。在样本数量明显不平衡的情况下，评价不平衡学习方法的指标显得尤为重要，而评价参数MCC能够反映不平衡学习的预测综合性能，因此，得到最佳MCC值就对应最佳阈值。
3 结果与分析讨论
3.1 优化滑动窗口矩阵
由于邻近蛋白质残基有相互影响，采用滑动窗口增加蛋白质空间局部信息，进行MCC参数最优选取，如图3所示。由图3所示，MCC值随着滑动窗口从3～17时不断上升，期间上升较为平滑，其主要归因于蛋白质ATP227数据量较大，滑动窗口从17之后MCC值开始下滑，即17为LPSSM的滑动窗口大小的最优值，则对应的特征维数即340（[17×20]）。
3.2 性能分析
通过5重交叉验证获取预测值，实验发现选取阈值T=1.433时，指标MCC最大。通过参考阈值最优（1.433）时的4项评价指标，非经过逻辑斯蒂标准化之前的数据（OriginalPSSM[30]）与经过逻辑斯蒂标准化之后的数据（LPSSM在2.2.2节已介绍）进行比较，如表1所示，可以发现LPSSM比OriginalPSSM四项指标都要高，特别是MCC中要高出约9%，这个效果还是比较明显的。
与ATPint，ATPsite，NsitePred，SVRATP（使用支持向量回归方法）进行比较，其中SVRATP未经过下采样处理，经过下采样后处理的方法称为RUS_SVRATP（random under?sampling，RUS），如表2所示。
首先，从SVR和前三种方法（非SVR）比较的角度可以发现：
（1） SVRATP和RUS_SVRATP明显优越于ATPint，SVRATP在四项评价指标中均优于ATPsite；
（2） SVRATP的MCC值为0.544，其分别高于ATPsite、NsitePred各11%和8%。另外NsitePred是最近发布的蛋白质?ATP绑定位点预测方法，但SVRATP略优于NsitePred；
（3） 虽然RUS_SVRATP相比ATPsite、NsitePred、SVRATP在Spe和Acc均略低，但是MCC值为0.609分别高出前者17%，14%，6%。
本文也在表2中用到t检验[31]，如果产生的p值是低于显著水平（0.05），那么不同表现的两种方法就可以认为具有统计意义。其次，从SVR角度看：
（1） 数据方面，RUS_SVRATP比SVRATP的MCC值要好，可能因为不平衡数据经过随机下采样后为平衡数据，负样本对训练中的模型干扰减少，模型更优，所以得到预测结果更好；
（2） 预测方面，SVRATP与RUS_SVRATP两者实验结果较好得益于SVR预测结果为连续实数，更加有利于最优阈值选取。
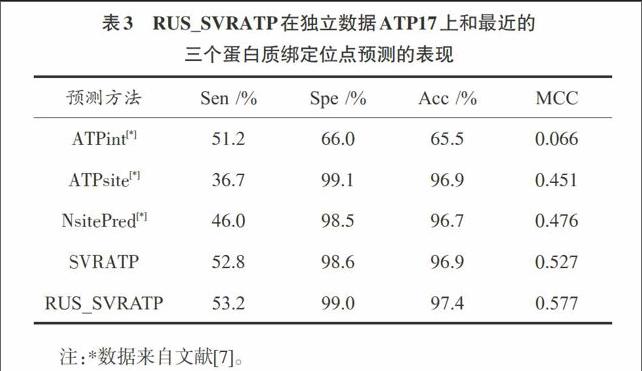
在独立数据集中与不同的蛋白质?ATP绑定位点预测方法进行比较，如表3所示，可看出：
（1） 显然RUS_SVRATP在独立测试数据集中表现最好；
（2） 其中RUS_SVRATP的MCC值比表现较好的NsitePred高出10%，另外和其他三项评价指标Sen、Spe、Acc都要比其他三个预测方法效果要好，分别高出7.2%，0.5%，0.7%；
（3） 另外SVRATP实验结果跟前三种方法对比也较好，这表明SVR对于蛋白质?ATP残基具有良好的预测效果；
（4） 从泛化能力角度看，随机下采样后的平衡数据比不平衡数据的数量更少，训练次数更少，预测结果更优，泛化能力更强。
3.3 讨 论
本文方法性能的改进主要得益于：
（1） logistic标准化处理后使正负样本更具代表性；
（2） 不平衡数据经过随机下采样后为平衡数据，负样本对训练中的模型干扰减少；
（3） 最重要的一点是用SVR预测模型预测置信度水平的方法取代了传统的硬分类。
除了以上3点主要原因，还有以下两种因素：
（1） 在本次实验中，最近公布的Swiss?Prot（www.ebi.ac.uk/swissprot）组合了更多的蛋白质序列数据库信息，更加有利于PSI?BLAST[24]方法搜索，因此可以提供更加准确的蛋白质进化信息；
（2） 选择核函数时，SVR的性能是由正则化参数和核参数影响的，考虑到这个问题，实验中在两个阶段尽可能的优化这两个参数，首先通过反复实验初步确定网格搜索的间隔，然后对网格搜索间隔进一步优化。最终得到c和g两个参数其值分别为1和0.6。
从以上实验结果可以看出，本文所述方法较之前提出方法[5?7]有一定提升，可为相关领域的研究人员特别是生物信息学方面的研究者提供一个新的研究思路，在这类问题的背景中，某个待识别样本的类别归属不仅取决于自身属性，也在很大程度上受到上下结构环境的影响，这时可以采取建立回归模型预测类别归属置信度的方法，即用回归预测取代传统的硬分类，会获得较好的分类效果。
4 结 语
本文采用从蛋白质的序列出发，首先使用滑动窗口抽取序列中每个残基的特征；其次应用随机下采样策略，消除正负样本存在的显著不平衡；最后建立支持向量回归模型进行预测，并选取最优阈值来判定蛋白质序列中的每个残基是否是蛋白质?ATP绑定位点，从而得到最终的预测结果。实验从特征提取方法、随机下采样方法和预测方法三个角度进行比较，实验结果表明基于随机下采样和支持向量回归的方法有效地提高了预测精度。
未来的工作包括两个方向：
（1） 通过合并新的特征提取方法和较优的分类器方法进一步提高RUS_SVRATP预测精度。例如基于回归的逻辑斯蒂L1标准化特征提取方法[32]已经成功用于活性位点预测；基于多重序列校准的稀疏逆协方差估计方法已经成功用于结构关系预测[33]。这两种新方法为提高RUS_SVRATP预测精度提供了研究方向。
（2） 除了研究ATP，还有其他绑定配体类型如金属离子、维生素、二硫键等，因此有效地区分不同类型的绑定配体的绑定机制也为进一步的研究提供了思路。
参考文献
[1] CAMPBELL N A， WILLIAMSON B， HEYDEN R J. Biology： exploring life [M]. [S.l.]： Recording for the Blind & Dyslexic， 2006.
[2] MAXWELL A， LAWSON D M. The ATP?binding site of type II topoisomerases as a target for antibacterial drugs [J]. Current Topics in Medicinal Chemistry， 2003， 3（3）： 283?303.
[3] 史忠植.高级人工智能[M].北京：科学出版社，2011.
[4] NOBELI I， LASKOWSKI R A， VALDAR W S J， et al. On the molecular discrimination between adenine and guanine by proteins [J]. Nucleic Acids Research， 2001， 29（21）： 4294?4309.
[5] CHAUHAN J S， MISHRA N K， RAGHAVA G P S. Identification of ATP binding residues of a protein from its primary sequence [J]. BMC Bioinformatics， 2009， 10（1）： 1?9.
[6] CHEN K， MIZIANTY M J， KURGAN L. ATP site： sequence?based prediction of ATP?binding residues [J]. Proteome Science， 2011， 9（1）： 1?8.
[7] CHEN K， MIZIANTY M J， KURGAN L. Prediction and analysis of nucleotide?binding residues using sequence and sequence?derived structural descriptors [J]. Bioinformatics， 2012， 28（3）： 331?341.
[8] HE H， GARCIA E A. Learning from imbalanced data [J]. IEEE Transactions on Knowledge and Data Engineering， 2009， 21（9）： 1263?1284.
[9] ZHOU Z， LIU X. ON Multi?class cost?sensitive learning [J]. Computational Intelligence， 2010， 26（3）： 232?257.
[10] ALTIN?AY H， ERG?N C. Clustering based under?sampling for improving speaker verification decisions using AdaBoost [C]// Structural， Syntactic， and Statistical Pattern Recognition. Berlin Heidelberg： Springer?Verlag， 2004： 698?706.
[11] 邓乃扬，田英杰.支持向量机：理论、算法与拓展[M].北京：科学出版社，2009.
[12] 孙德山.支持向量机分类与回归方法研究[D].长沙：中南大学，2004.
[13] 隋海峰，曲武，钱文彬，等.基于混合 SVM 方法的蛋白质二级结构预测算法[J].计算机科学，2011，38（10）：169?173.
[14] YU D J， HU J， TANG Z M， et al. Improving protein?ATP binding residues prediction by boosting SVMs with random under?sampling [J]. Neurocomputing， 2013， 104： 180?190.
[15] ZHANG Y N， YU D J， LI S S， et al. Predicting protein?ATP binding sites from primary sequence through fusing bi?profile sampling of multi?view features [J]. BMC Bioinformatics， 2012， 13（1）： 118?125.
[16] CHEN K， MIZIANTY M J， KURGAN L. Prediction and analysis of nucleotide?binding residues using sequence and sequence?derived structural descriptors [J]. Bioinformatics， 2012， 28（3）： 331?341.
[17] YU D， HU J， YANG J， et al. Designing template?free predictor for targeting protein?ligand binding sites with classifier ensemble and spatial clustering [J]. 2013， 10（4）： 994?1008.
[18] YU D J， HU J， HUANG Y， et al. Target ATP site： A template?free method for ATP?binding sites prediction with residue evolution image sparse representation and classifier ensemble [J]. Journal of Computational Chemistry， 2013， 34（11）： 974?985.
[19] FIROZ A， MALIK A， JOPLIN K H， et al. Residue propensities， discrimination and binding site prediction of adenine and guanine phosphates [J]. BMC Biochemistry， 2011， 12（1）： 20?28.
[20] 陈义明，李舟军，刘军万.改进LPU 用于蛋白质功能预测[J].计算机工程与科学，2012（12）：148?152.
[21] YU D J， SHEN H B， YANG J Y. SOMPNN： an efficient non?parametric model for predicting transmembrane helices [J]. Amino Acids， 2012， 42（6）： 2195?2205.
[22] PIERLEONI A， MARTELLI P L， CASADIO R. MemLoci： predicting subcellular localization of membrane proteins in eukaryotes [J]. Bioinformatics， 2011， 27（9）： 1224?1230.
[23] SHEN H B， CHOU K C. A top?down approach to enhance the power of predicting human protein subcellular localization： Hum?mPLoc 2.0 [J]. Analytical Biochemistry， 2009， 394（2）： 269?274.
[24] SCH?FFER A A， ARAVIND L， MADDEN T L， et al. Improving the accuracy of PSI?BLAST protein database searches with composition?based statistics and other refinements [J]. Nucleic Acids Research， 2001， 29（14）： 2994?3005.
[25] WEISS G M， PROVOST F. The effect of class distribution on classifier learning： an empirical study [D]. USA： Rutgers University， 2001.
[26] LAURIKKALA J. Improving identification of difficult small classes by balancing class distribution [M]. Berlin Heidelberg： Springer， 2001.
[27] ESTABROOKS A， JO T， JAPKOWICZ N. A multiple resampling method for learning from imbalanced data sets [J]. Computational Intelligence， 2004， 20（1）： 18?36.
[28] CHANG C C， LIN C J. LIBSVM： a library for support vector machines[J/OL]. [2001?06?01]. http：//?www.?csie.?ntu.?edu.tw/?～ cjlin/? libsvm.
[29] 孔英会，景美丽.基于混淆矩阵和集成学习的分类方法研究[J].计算机工程与科学，2012（6）：111?117.
[30] SHEN H， CHOU J J. MemBrain： improving the accuracy of predicting transmembrane helices [J]. PloS one， 2007， 3（6）： 2399?2399.
[31] YANG J， ZHANG L， YANG J， et al. From classifiers to discriminators： a nearest neighbor rule induced discriminant analysis [J]. Pattern Recognition， 2011， 44（7）： 1387?1402.
[32] SANKARARAMAN S， SHA F， KIRSCH J F， et al. Active site prediction using evolutionary and structural information [J]. Bioinformatics， 2010， 26（5）： 617?624.
[33] JONES D T， BUCHAN D W A， COZZETTO D， et al. PSICOV： precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments [J]. Bioinformatics， 2012， 28（2）： 184?190.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 21:21:30