例谈构造法在数学解题中的应用

    沈重

    

    

    

    [摘要]“构造法”是数学解题的有效方法，构造法四种最常见的形式为方程构造法、图形构造法、函数构造法和数列构造法，探讨构造法在数学解题中的应用能提高学生的解题能力，

    [关键词]构造法，解题，应用

    [中图分类号]G633.6[文献标识码]A [文章编号]1674-6058（2020）11-0012-03

    构造法是指当某些数学问题按照定式思维思考不出结果时，转变到另一个角度去寻找问题的数量、结构、条件与结论间的关系特征等，从而构造出新的数学对象或问题形式，使原来隐晦不清的特性在新构造出的数学对象或问题形式中清晰地展现出来，达到简捷地解决数学问题的目的，构造法是数学解题的有效方法，本文主要探讨构造法在数学解题中的原则与应用。

    一、构造法的解题原则

    1.相似性原则

    相似性原则指由题目中的题设条件启发，联想此前已经学过的相似内容，进而通过构造法将现有题目和熟悉的内容建立起联系，

    [例1]证明a>0.b>0.则a3+b3≥3ab，

    分析：可以联想相似的基本不等式a3+b3≥2ab，通过利用与其相似的方法证明该题的不等式，即由（a+b）3≥0得出a3+b3≥3ab，

    2.直观性原则

    直观性原则，指通过构造一种数学形式或实际模型，使得题设条件与结论之间的关系很明显地显现出来，

    从上述例题可以发现，与一元二次方程构造有关的往往是根与系数的判别式△=b2-4ac，解题时须密切关注与之相似或有关的条件，借以构造适当的方程辅助解题，

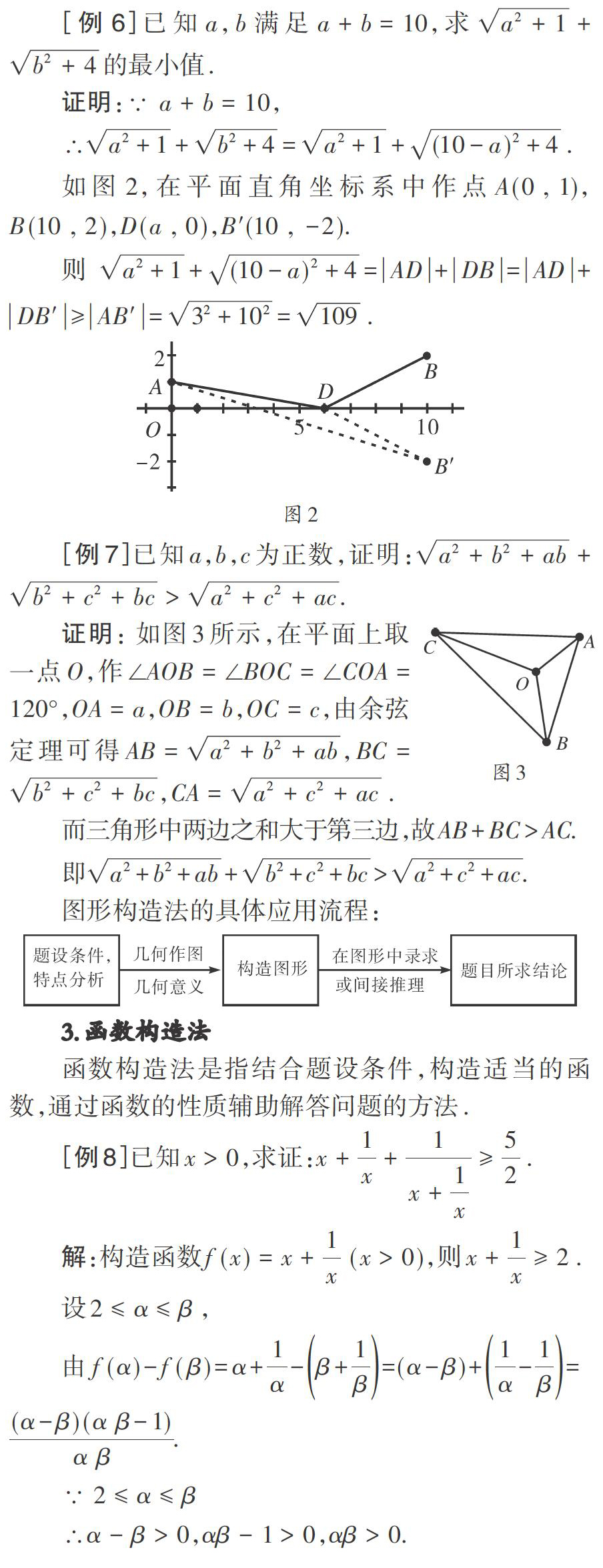
    2图形构造法

    图形构造法是指当问题条件的数量关系有明显的几何意义或能以某种方式将问题转化为几何图形时，可以借助几何图形的性质研究，从而获得问题的解法，

    3.函数构造法

    函数构造法是指结合题设条件，构造适当的函数，通过函数的性质辅助解答问题的方法，

    许多看似与函数无关的题目，其实都可以巧妙地通过构造函数的方法解答，构造函数之后，便涉及函数的单调性和求导等知识的运用，因此，函数构造法是另一种极为重要的解题方法。

    4.数列构造法

    用构造法求数列的通项公式是比较巧妙的方法，构造数列可以构造等比数列和等差数列，其中构造等差数列还包括构造常数列这一特殊情况，

    高中的数列以等差数列和等比数列为主，但题目中往往不会一目了然地给出这两种形式的数列，这时候就需要用到构造法，将题设中复杂的形式通过构造法转化成我们所熟悉的数列形式。

    三、总结及教学建议

    构造法往往能巧妙地化解许多看似无从下手的问题，但是，构造法的解题思路属于非常规思路，虽有原则可循，卻无固定的解题方法，常常需要靠学生的“顿悟”，而这其实也是对一个人创造性思维的一种考验，如今，课程标准也越来越重视对学生创造性思维的培养，所以训练数学构造法也是培养学生创造性思维的一种重要方式。

    教师可适当将构造法融入教学中，比如将其作为一题多解中的一种解法来讲解，由于构造法对解题思维的要求较高，教师最好在展示解题方法的过程中适当暴露思维过程，这样更能让学生了解解题过程中每一个步骤的由来及知识应用的目的。