2016年山东高考数学文科立体几何解法赏析
王义东
立体几何既是高中数学的重点内容,又是高考的必考内容,每年高考试题中都有一道立体几何解答题,通过柱体、锥体、台体或不规则的多面体,来考查考生的空间想象能力、逻辑思维能力和运算能力.本题主要考查证明线面平行及线面垂直.
2016年山东高考文科试题
(18)(本小题满分12分)
在如图1所示的几何体中,D是AC的中点,
EF∥DB.
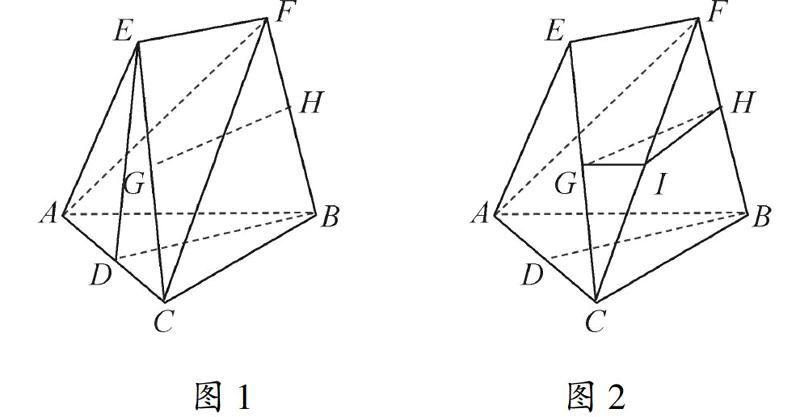
(Ⅰ)已知AB=BC,AE=EC.求证:AC⊥FB;
(Ⅱ)已知G、H分别是EC和FB的中点.
求证:GH∥平面ABC.
证明(Ⅰ)因为EF∥DB,所以EF与DB确定平面BDEF.
连接DE,因为AE=EC,D为AC的中点,所以DE⊥AC.
同理可得BD⊥AC.
又BD∩DE=D,所以AC⊥平面BDEF.
因为FB平面BDEF,所以AC⊥FB.
说明:学生主要存在的问题是对线面垂直的判定不熟悉,没有说明EF与DB确定平面BDEF.另外学生出现字母的笔误较多.
典型问题:没有说明GHMN四点共面.
法五如图6,设AE,AF的中点为M、N,连接MN,NH,GN,MG∥AC,MN∥EF∥BD,面MNG∥面ABC,NG∥面ABC,NH∥AB,NH∥面ABC,面NHG∥面ABC,GH∥面ABC.
典型问题:没有说明MNHG四点共面.
思路二是通过证明线线平行,利用线面平行的判定定理进一步得到线面平行.
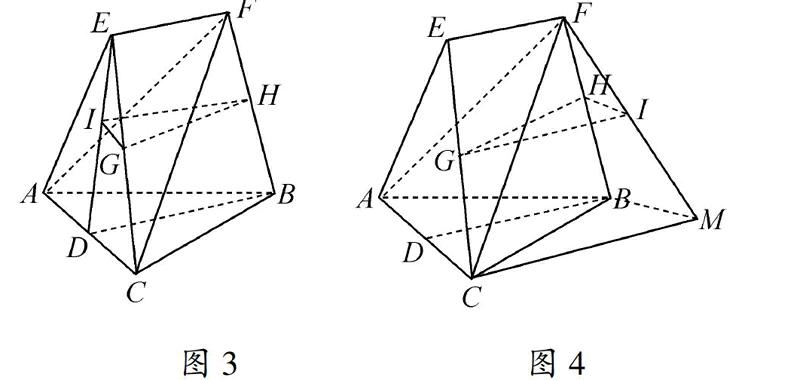
典型错误:学生空间想象能力差,出现GH∥BC,GH∥BD.
总之,文科立体几何的解答题往往通过构建规则的柱体、锥体、台体和不规则的多面体,证明线线、线面、面面的平行或垂直,考查学生空间想象能力、逻辑思维能力.在立体几何解答题的解题过程中,如面面平行(或垂直)转化为线面平行(或垂直),再转化为线线平行(或垂直);在复习中一定掌握平行或垂直的判定及性质,通过强化训练,把握解题的规律,逐步培养空间想象能力,提高逻辑思维能力,提升思维品质,只有这样,在解决问题时,才能触类旁通,举一反三.
立体几何既是高中数学的重点内容,又是高考的必考内容,每年高考试题中都有一道立体几何解答题,通过柱体、锥体、台体或不规则的多面体,来考查考生的空间想象能力、逻辑思维能力和运算能力.本题主要考查证明线面平行及线面垂直.
2016年山东高考文科试题
(18)(本小题满分12分)
在如图1所示的几何体中,D是AC的中点,
EF∥DB.

(Ⅰ)已知AB=BC,AE=EC.求证:AC⊥FB;
(Ⅱ)已知G、H分别是EC和FB的中点.
求证:GH∥平面ABC.
证明(Ⅰ)因为EF∥DB,所以EF与DB确定平面BDEF.
连接DE,因为AE=EC,D为AC的中点,所以DE⊥AC.
同理可得BD⊥AC.
又BD∩DE=D,所以AC⊥平面BDEF.
因为FB平面BDEF,所以AC⊥FB.
说明:学生主要存在的问题是对线面垂直的判定不熟悉,没有说明EF与DB确定平面BDEF.另外学生出现字母的笔误较多.
典型问题:没有说明GHMN四点共面.
法五如图6,设AE,AF的中点为M、N,连接MN,NH,GN,MG∥AC,MN∥EF∥BD,面MNG∥面ABC,NG∥面ABC,NH∥AB,NH∥面ABC,面NHG∥面ABC,GH∥面ABC.
典型问题:没有说明MNHG四点共面.
思路二是通过证明线线平行,利用线面平行的判定定理进一步得到线面平行.

典型错误:学生空间想象能力差,出现GH∥BC,GH∥BD.
总之,文科立体几何的解答题往往通过构建规则的柱体、锥体、台体和不规则的多面体,证明线线、线面、面面的平行或垂直,考查学生空间想象能力、逻辑思维能力.在立体几何解答题的解题过程中,如面面平行(或垂直)转化为线面平行(或垂直),再转化为线线平行(或垂直);在复习中一定掌握平行或垂直的判定及性质,通过强化训练,把握解题的规律,逐步培养空间想象能力,提高逻辑思维能力,提升思维品质,只有这样,在解决问题时,才能触类旁通,举一反三.

