高中数学教学中学生核心素养培养途径探究

    陈红梅

    

    

    摘要：概念教学是高中数学的重点内容，只有牢固掌握与理解数学概念，才能正确灵活应用。在当前大力提倡培养学生核心素养的背景下，应做好高中数学概念的研究，把握核心概念，结合核心素养相关内容，寻找相关的教学策略，使学生在掌握核心概念的同时实现核心素养的提升。

    关键词：高中数学 ?核心素养 ?培养 ?核心概念

    高中数学涉及的很多核心概念，是学习与解决数学问题的重要基础，主要有集合、函数、数列以及立体几何中的相关概念等。这些概念本身并不难记忆与理解，但要想灵活应用并非易事。授课中应做好核心概念教学与核心素养培养之间的研究，积极采取有效策略，将核心素养培养工作融入到核心概念教学的各个环节。

    一、借助集合教学，培养数学抽象素养

    集合是高中数学的核心概念，贯穿整个高中数学。学生掌握集合概念的深度给高中数学学习成绩带来的影响较为明显。授课中深挖集合内涵，使学生真正地掌握集合本质，并能灵活运用所学集合知识表征数量与数量、图形与图形之间的关系，实现数学抽象素养的提升。一方面，要求学生认真学习教材中有关集合概念的描述，不仅要准确掌握相关的符号，而且应充分理解其性质以及集合之间的关系，为其从集合视角分析相关问题奠定坚实基础。另一方面，围绕集合概念以及相关知识，创设相关的问题情境，要求学生根据所学合理地抽象，运用集合知识正确表征事物的规律与结构。

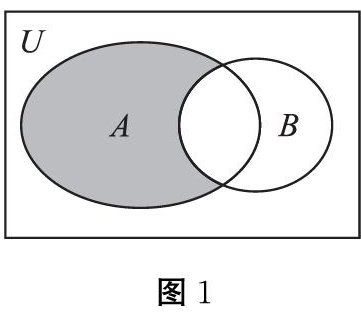
    例1，设全集为U，集合A和B，如图1所示，则阴影部分可用以下哪个集合表示（ ?）

    A.A∪（CUB） ? ?B.A∩（ CUB）

    C.（ CUA）∩B ? D. CU（A∩B）

    该题目要求学生根据图形之间的关系，运用所学的集合知识加以正确的表征，不仅检验了学生对集合概念的理解深度，而且有助于学生直观想象素养的培养。认真观察图1可知阴影部分在集合B外，但在集合A中，因此，可用A∩（ CUB）进行表征，正确选项为B。

    二、借助函数教学，培养数学建模素养

    函数在高中数学中占有重要地位，描述的是自变量与因变量之间逻辑关系。为使学生深刻理解函数概念，灵活应用于解答相关试题中，并在学习中提升数学建模素养。一方面，认真讲解函数定义域、对应法则、值域以及性质等基础知识，使学生不仅认识函数，更要帮助其树立运用函数知识求解问题的观念。同时，讲解构建函数模型应注意的细节，不断提高函数应用能力。另一方面，為在函数教学中培养学生的数学建模素养，应注重设计相关的问题对学生进行训练，使其从问题中提炼有效信息，亲身体会数学建模的整个过程，积累数学建模的方法与经验。

    例2，研究发现，某海鲜加工公司的当月产量在10吨～25吨时，月总成本y（万元）可以看成月产量x（吨）的二次函数。当月产量为10吨时，月总成本20万元。当月产量为15吨时，月总成本最低，为17.5吨。已知该产品销售价为每吨1.6万元，则月产量为多少时，可获得最大利润？

    通过认真审题，提取题干中的有用信息可知，解答该题目需要构建月总成本y（万元）和月产量x（吨）之间的一元二次函数模型。通过该题目的训练，构建函数模型时应注重确定正确的定义域范围。

    三、借助数列教学，培养逻辑推理素养

    高中阶段学习的数列概念主要有等差与等比数列。无论是等差数列还是等比数列，学生均能轻易地掌握相关概念，但高中数学有关数列的情景复杂多变，较为抽象，学生学习难度较大。为使学生牢固地掌握与理解数列概念及其相关知识，授课中应注重以下内容的落实：一方面，引导学生采用对比记忆法，记忆等差与等比数列的相关性质，并鼓励其做好通项公式以及前n项和求解方法的总结，扎实掌握有关数列的基础知识，深化对数列概念的理解。另一方面，等差数列与等比数列较为类似，因此授课中应注重围绕相关的问题情境，为学生讲解类比推理相关知识，使其能够运用所学合理的类比，得出正确的推理结论，促进其逻辑推理素养的提升。

    例3，在等差数列{an}中，前n项和Sn=a1+a2+…+an=n（a1+an）2=na1+n（n-1）2d，类比这一性质，则在等比数列{bn}中前n项的积Tn= ? ?。

    该题目较为新颖，考查了学生对等差、等比概念的理解以及类比推理能力，能很好地锻炼学生的逻辑推理能力。授课中，应要求学生认真回顾等差数列前n项和的推导过程，进行合理的类比推理，推导出等比数列前n项积的表达式。学生通过思考类比出Tn=b1·b2·…·bn=（b1·bn）n2=b1n·qn（n-1）2。该类比推理结论是否正确呢？下面进行推导：Tn=b1b2…bn=b1·b1q·…·b1qn-1=b1n·q·q2·…·qn-1=b1n·qn（n-1）2，则可知类比推理的结果是正确的。

    四、借助立体几何教学，培养直观想象素养

    立体几何是高中数学的重要章节，涉及的概念多而复杂。授课中应灵活运用多种授课方法帮助学生理解相关概念，搞清概念之间的内在关系，为培养其直观想象素养做好铺垫。一方面，授课中可应用多媒体技术直观地展示点、线、面等相关元素，或引导学生想象生活中的事物，进行合理的联想与抽象，搞清楚与立体几何相关的概念，帮助学生建立空间立体感。另一方面，结合自身授课经验，注重选择相关的问题，要求学生利用几何直观以及空间想象，对事物的形态变化加以合理把握，寻找解决问题的突破口，夯实其所学知识的同时，促进其直观想象素养的提升。

    例4，已知某几何体的三视图如图2所示，则该几何体的外接球的表面积为（ ?）

    A.π ? B.2π ? C.3π ? D.4π

    该题目要求学生根据给出的几何体的三视图，认真分析各面之间的关系，进行合理的空间想象，还原出相关的几何体，而后求出其外接球的表面积，不仅加深学生对立体几何相关核心概念的理解，而且能很好地培养学生的直观想象素养。认真观察给出的三个视图，可知该几何体是一个以俯视图为底面的三棱锥。通过绘制相关的草图不难得知，该几何体的外接球相当于一个长、宽、高分别为2，1，1的长方体的外接球，则外接球的半径r=2+1+12=1，则该球的表面积为S=4π·r2=4π，正确选项为D。

    培养学生核心素养是新课改的重要目标之一，因此，高中数学核心概念教学中，应注重核心素养培养工作的渗透，既要做好高中数学核心概念的归纳与分析，又要积极探寻有效策略，将核心概念教学与核心素养培养工作有机融合，使学生在学习、掌握核心概念的同时提升核心素养。

    参考文献：

    [1]张银龙.浅谈高中数学教学中学生核心素养的培养[J].数学学习与研究，2019（19）：97.

    [2]安文勇.高中生物教学中学生核心素养的培养途径[J].甘肃教育，2019（18）：178.

    [3]李玉杰.高中数学教学中学生核心素养的培养策略研究[J].课程教育研究，2019（25）：143.

    [4]吕升斗.高中数学课堂教学中学生核心素养的培养[J].基础教育论坛，2019（04）：42-43.

    [5]肖绍良.数学教学中学生核心素养的形成及培养途径[J].数码设计，2017，6（09）：187-188.