计算归简 分合衍变

    费海明

    

    

    

    “计算思维”概念自进入教育视野后，备受关注。但在教学实践中，教师对“计算思维”有不同的理解。一部分教师将“计算思维”视为计算机科学概念的大集合，把教学如剪贴板、驱动程序、邮件传输等视同计算思维教育的分解;而另一部分教师则将“计算思维”与“程序算法”画上约等号。起初不起眼的微小的理解差异，经过多次迭代，最终会发展成截然不同的实践结果。鉴于此，笔者认为需要追根溯源，透析计算思维的内在要素，追问计算思维教育的最终目的，才能在理解的基础上，生发教学的创意。

    计算思维的内涵与追求

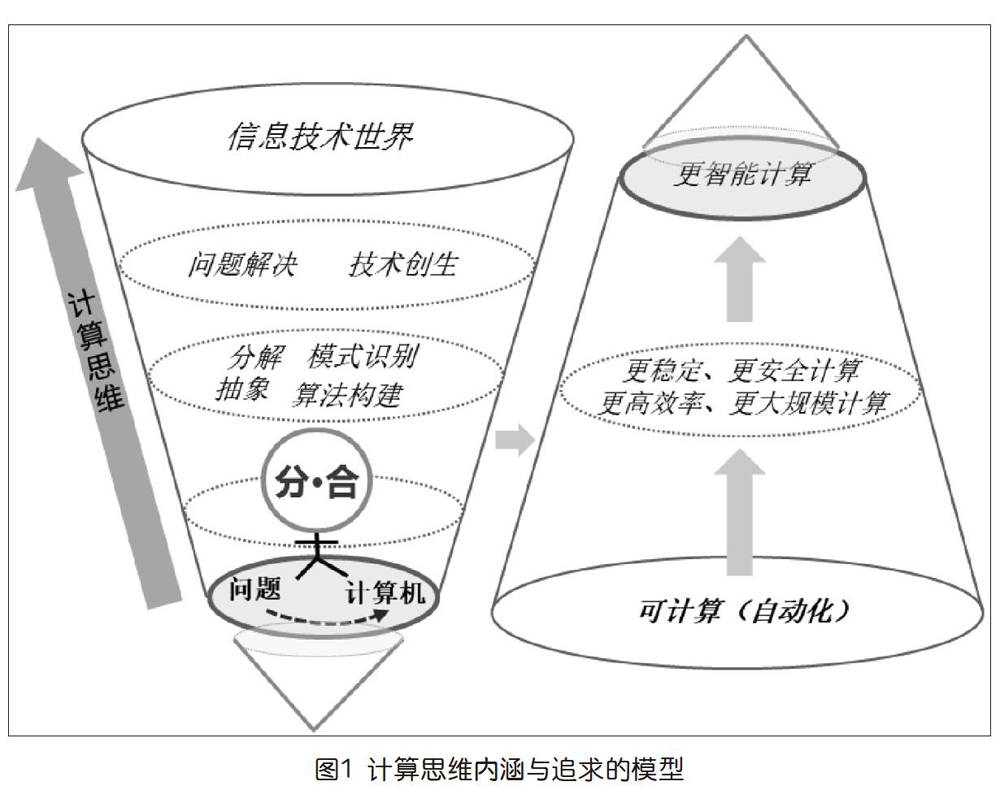
    对计算思维内涵的理解，可追溯至图灵时代。图灵将机器的操作分解为“最基本操作”，以至于不能再分解，让机器从一个无限长的纸带中读取符号序列（将要求解的数转换为机器可识别的符号），机器逐一执行“最基本操作”，最终实现计算的自动化。现代计算机的计算不仅要实现自动化，更要追求高效率、大规模、更稳定、更安全、更智能的计算，这是创造性思维向着“可计算”的方向不断迸发与迭代的过程。如要做到多任务，那就要让CPU“分时”;大规模的数据要快速排序，那就会用到“分治”的算法思想;传输大文件，可将文件“分段”发到目的地后再“重组”;想要让更多的用户同时在线访问，那就将服务器“分身”，用分布式、读写分离和协调器等技术应对大规模计算。

    计算思维（狭义）究其本质，是确定问题的“可计算”部分及“问题解决方案”至“计算机可执行方案”这二者之间实现转化与创造的思维过程。这一过程富有挑战性，是一个分解、抽象、模式识别和算法构建的思维过程，充满了“分合衍变”的辩证思想。为计算而分之，又为目的而合之。合中生分，分而治之，分合复始，“分与合”的组合与衍化，使得“问题解决方案”向着“可计算方案”不断转化与优化，创生出信息技术世界的实体与具体概念，如图1所示。

    “计算思维+”视野下的教育融合

    计算思维的培育应融入教育整体和信息技术学科的核心素养培育过程。

    首先，计算思维可以与其他思维培育相融合。当学生经历问题的逐步分析和抽象时，就是在培育逻辑思维;当学生发现原系统功能或算法的不足，用计算思维进行优化改进时，就是在激发创造性思维。

    其次，计算思维可以与学科三大核心素养培育相融合。信息技术的核心素养包括计算思维、信息意识、数字化学习与创新和信息社会责任四大部分。在“计算思维+”的视野下，信息意识追求的是识别重复结构、发现冗余结构、洞察内在结构、觉察信息背后数据、推断功能背后算法的“意识”;数字化学习与创新就是用计算思维审视现存系统和现实问题的学习与创新;信息社会责任则是对技术与信息的创造者的正能量的宣扬、感悟和仿效，以计算思维为“透镜”，增强技术防护意识，自觉维护数字社会的安全。这样，在计算思维的加持下，各核心素养内涵进一步丰富，其培育得以整体优化。

    中小学计算思维培育的切入点

    对于中小学信息技术教育而言，以项目为载体开展计算思维教育，从具象到抽象，具有可操作性。在项目实践中，教师要有超越具体的项目和技术的意识，通过优化、逆构等视角，引导学生向着“可计算”的方向展开思维过程，并不断反思，从而实现计算思维的内生与发展。

    1.优化视角——在项目实施中渗透计算思维

    优化就是面向更优异目标的一种思考与行动，一种最优解的追求。应用优化视角，可以引导学生对原方案（算法）进行审视，应用抽象、分解和模式識别，实现原方案（算法）的重构或改进。

    案例1：作文集“优化记”。

    第一步：抽象。先不考虑作文集的主题、篇数、文本和插图，也不考虑用Word还是WPS，只考虑作文集要处理（计算）的基本要素——标题、署名、正文等。

    第二步：分解。将作文集项目制作逐步分解，分解至“能清晰地与字处理软件的具体工具对应”为止。

    第三步：模式识别。在分解的基础上，思考：哪些设置属于同类项，可以合并？哪些是属于默认设置，可以忽略？

    第四步：算法构建。在模式识别的基础上，优化作文集的制作流程（算法），如下页图2所示。

    通过对项目的要素与步骤的分解，可以引导学生发现相似、相同的部分并加以统整，避免表示的冗余或操作的重复，以实现问题解决（算法）的优化。例如，作文集的文字格式设置是一项不小的工程，很值得优化研究;而制作PPT的过程中是新建还是复制某页基础上修改，这事实是“哪种方案最优”的思考，是一种优化视角下的分解和模式识别。

    2.逆构视角——在原理探究中发掘计算思维

    逆构，是由果索因，是指从现有的技术思考该技术的实现过程。逆构视角不是关注技术的应用，而是关注技术工具的“重新发明”，即让学生体验技术开发者的计算思维过程，感受开发者的智慧和精神。

    案例2：Excel填充柄诞生记。

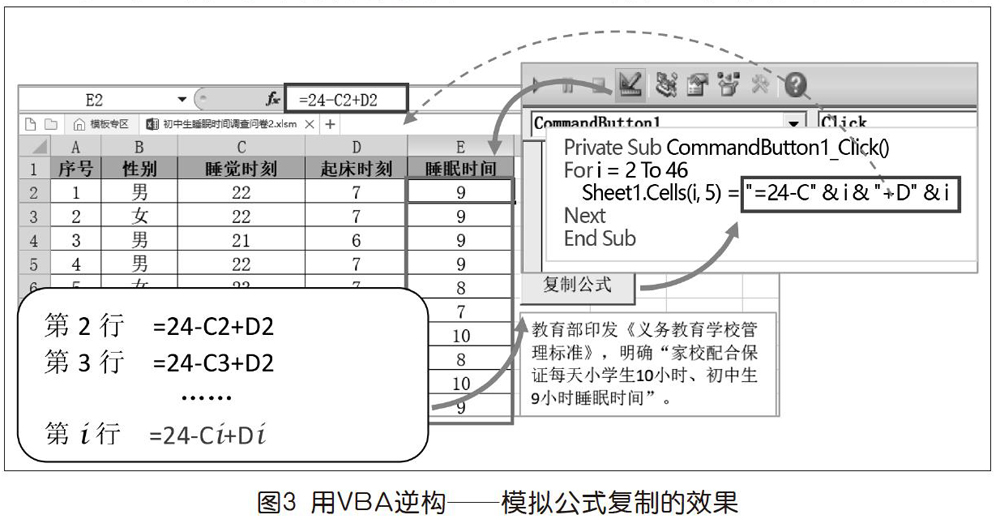
    在“初中生睡眠时间调查统计”项目中，教师提问：“填充柄如何实现公式的自动复制？”学生通过列出E列单元格上的一部分公式，提炼出“通项”公式“=24-Ci+Di”。接着，教师将提炼出的公式转换成VBA代码，并用循环结构令其“反复做”，当按下按钮那一刻，学生惊奇地发现——填充柄诞生了（如图3）。

    抽象出来的公式与最终的VBA代码形式，会略有差异，但其结构是一致的。人脑中的算法转化至机器内能运行的符号表达，算是一种“入乡随俗”。要让机器执行人脑的算法思想，则必须与机器中已人为预置的、已抽象的协议或接口“打交道”，这与图灵思考的“可计算”的本质是一样的。

    以逆构视角观察，计算思维研究和讨论的资源变得无处不在，自然也就取之不尽，用之不竭。例如，Word文字居中——逆构“字符串居中算法”，未封闭图形的填充漏色现象——逆构“广度搜索”等。

    3.突围视角——在现实约束下激发计算思维

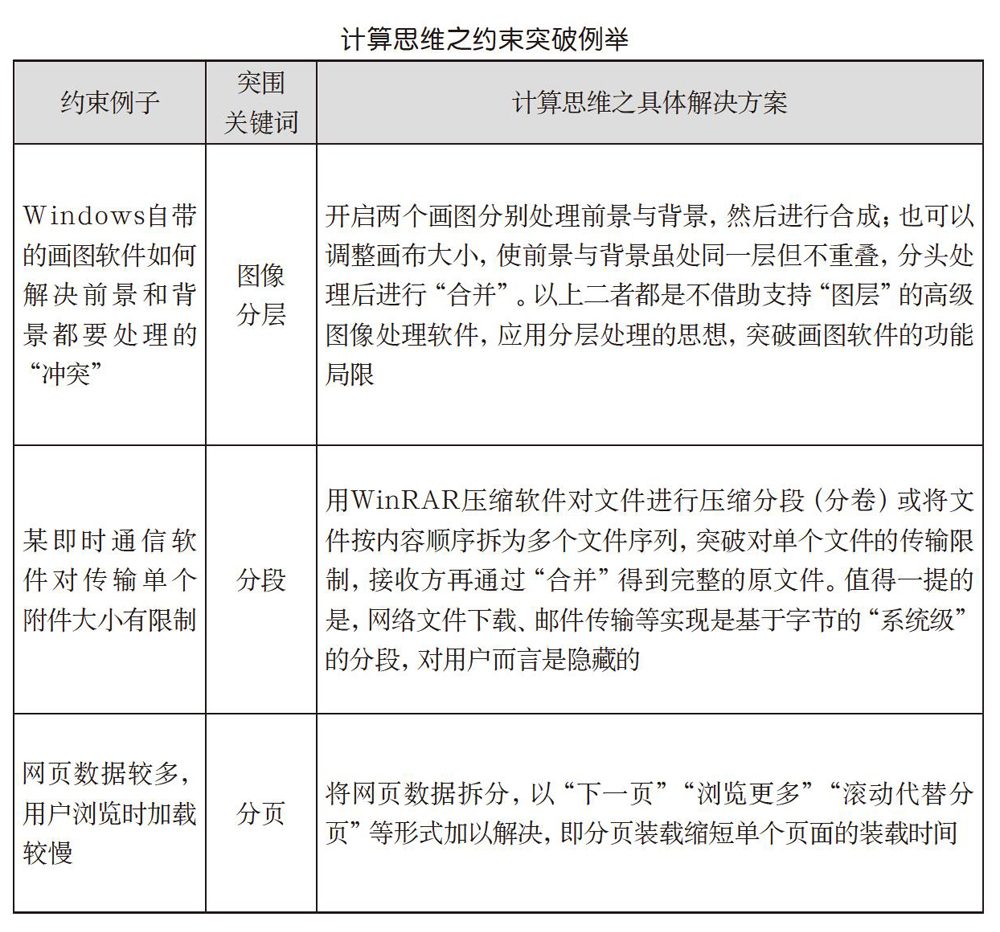
    突围就是突破困难或约束的思考与行动。在用计算机求解问题时，常会遇到存储速度、存储容量、计算速度、网络带宽等问题，这些困难限制了问题求解的规模、速度、稳定性和安全性。在实际教学中，教师可以构造一种模拟的约束情境，在不降低问题难度和更换计算资源的前提下，思考突破的方法——突围视角，这将极大地激发学生的计算思维。具体例子如下表所示。

    4.开发视角——在程序设计中培育计算思维

    开发指的是程序设计与开发，这也是较为经典的计算思维培育视角。程序开发是“原生”的计算思维孕育场，其明确而有限的指令（函数）、面向用户的交互设计、忠实如一的执行调试和朴素算法的不完美等体验，都会激发学生拿起“分解、模式识别、抽象、算法构建”的思维武器，为实现程序的诞生与升级而不断探索。

    案例3：抽奖盘——计算思维知多少。

    第一步：抽奖盘有哪些对象（角色）？它们有什么行为？学生发现转盘上的指针不能随着转盘转动，因此两者需要分离，对应于Scratch中的2个角色。

    第二步：转盘如何转动？在实践中学生发现，输入的度数是让转盘“瞬间定格”于最终度数，而非预想的“旋转”，而且该类指令不支持转动时间的设置，若要实现动画，只能对旋转的度数进行分解，让转盘每次只旋转一个小的角度（如15度），借助循环执行“合成”转动的动画。

    第三步：如何模拟出每次转盘停的位置不一样？用随机数指令即可，但随机数的取值范围与旋转执行次数之间有什么关系呢？可引导学生模式识别，转盘随机停留其本质上是360度范围内的随机取值。若想转动5圈后随机停，则随机数取为360÷15×5（120）～360÷15×6（144），如图4所示。

    以上构建的程序实现的转动是“生硬”的。对于初中生而言，鼓励学生用一次函数y=kx+b或正弦函数y=sin（x）实现缓动，如下页图5所示。此外，还可以借助人工智能技术，支持更友好的交互和更智能化的抽奖。

    计算思维培育的四大视角并不孤立存在，而是互相交融。“逆构视角”以现有技术为对象，乃是重新经历“开发（视角）”的过程;而“突围视角”何尝不是一种约束条件下指向内在的“优化（视角）”。教师拥有四大视角并实现互融，计算思维教育的点滴创意也就在教學实践中不断诞生。

    仔细观察眼前的现实世界，万物看似形态各异，但其内在结构与要素却有着惊人的相似。纷繁复杂的信息世界，谁会料到隐藏于后台的系统和映入眼帘的程序都来自“可计算”的初心。兼顾机器的特性，突破算力的限制，直至人的思维融入至人类自身创生的系统，无数的计算思维演绎出一场场“分与合”的演变，繁衍出层出不穷的技术、各具个性的项目和丰富多彩的信息，最终推动信息世界版本的分秒更迭。计算思维的“可结晶”、可分层、可迭代，正是预示着一场恢宏无比的全世界脑力联网的超智能演化。这一切可以看成是“生命为机器赋智能”，也可以视为“技术为生命赋活力”。计算思维的内涵是如此的深邃，而探索计算思维的教育是如此的充满挑战与乐趣。