初中数学函数教学中渗透模型思想的研究
王国云
[摘? 要] 文章详细阐述教师在初中数学函数课堂中,如何渗透模型思想,并结合具体案例讲述教学过程,旨在提升学生构建模型的能力.
[关键词] 初中数学;函数教学;模型思想
模型思想在一次函数教学中的运用,能帮助学生更快地解决问题,这也是新课程改革要求下常见的教学模式,能充分提高学生学习效率,在初中数学教学中有重要价值.
■ 初中数学函数教学中渗透模型
思想的过程
1. 发现问题
为了更好地将模型思想渗透到教学中,让学生可以自主构建模型并解答,教师在设计教学情境的时候,需根据学生已有经验与对一次函数的认知程度,以最近发展区为基础,以“经过努力,提升能力”为目标,科学构建情境,帮助学生建立数学模型. 而让学生在其中发现问题就是最开始的目的,基于学生的思维能力和年龄特点创设的情境,让其更容易接受直观性知识,在思考中解决问题,有助于数学模型的构建■.
2. 做出假设
在教师情境的构建中,让学生发现问题、分析问题,并能通过观察、分析、总结和归纳,对问题做出大胆假设. 学生在假设的过程中,可能出现问题,如假设错误或者不合理,教师此时不能急于否定,要相信学生,不怕其出现错误,只有经过自己不断思考和分析,设置假设内容,才有助于增强学生的创新能力和实现思维拓展. 对初中函数知识来说,学生可以结合题目中的已知条件和多种数据之间的关系,构建初步假设.
3. 建立模型
假设完成后,就要构建模型,利用函数关系式中的已知量和未知量,找出两者之间的关系,并通过数学符号表示出来,此过程就是模型建立的过程. 在整个教学中,构建模型是最关键的环节. 将有相等关系的数据构建成抽象的方程模型,解决生活中的问题,如商场中货物的销售、银行中多种存钱方案的选择问题等等;解决涉及几何的问题,如实际生活中工程定位、路程和航海问题等,需建立几何、代数模型;解决球赛胜负和彩票中奖问题,构建概率模型等. 初中阶段接触到的模型种类还有很多,本文主要针对一次函数模型进行研究,因为函数能反映事物之间的关系,也揭示了现实生活中的常见情况. 初中数学中函数部分是最难的,为了让学生更好地了解数学函数知识,还是需要教师在函数模型的构建上下功夫,让学生将生活内容和实践结合,建立函数模型,快速解决问题.
4. 求解模型
函数模型建立后,就要求解,运用学生已学知识,如通过等式的性质解方程,如果是不等式,则结合不等式的性质,解答几何模型的时候,则利用三角形性质,或者与图形有关的知识,化简方程式,解答函数模型,最终得到结果.
5. 验证模型
数学模型解答后,学生可能还不能深入发现问题,只是单一解答数学问题,而教师还要带领学生分析结果,将其代入实际问题中进行检验. 对学生来说,可以将结果代入模型和教师创建的问题情境中. 此处的检验呈现两种结果,一种是结果符合模型,说明模型可以使用,另一种是结果不符合模型,此时教师要鼓励学生分析,从假设问题开始到最后的求解模型,找出错误. 这一过程对学生来说有些困难,需要学生正视自己的问题,建立追究到底的信心,在教师的关注下,提升学习数学的严谨性和逻辑性,以正确的学习态度,增强学生学习的积极性.
6. 应用模型
验证结束后,不代表整个建模过程就完全结束,需要学生结合在建模过程中发现的问题,进行总结和反思,将建模过程内化. 现代社会的发展对学生的学习要求越来越高,因此教师要引导学生的思考不局限于其中某一知识点,而是利用模型的构建检测自己的学习情况,并运用建模思想,解决生活中更多的问题. 学生能够独立进行建模,体现了数学的应用价值,能增强学生的数学迁移能力,促进其健康、全面地发展.
■ “一次函数模型”案例分析
以一次函数为案例,介绍渗透数学模型教学过程.
1. 构建模型,发现问题
以弹簧为教学工具,在上面依次悬挂同质量的物品,边增加质量,边让学生观察,提问:“在老师增加物质质量的过程中,你们有什么发现?”回答:“弹簧越来越长. ”此过程就是发现问题. 教师接着提问:“那么请同学们分析,弹簧长度的变化,与什么原因有关?”学生经过思考得出答案:“与悬挂物品质量有关. ”这就是做出假设的过程. 然后教师利用实验过程,如弹簧原长为5厘米,挂上物品后,每增加1千克,弹簧的长度就增加0.6厘米,增加2千克,弹簧延长1.2厘米,问题:悬挂3千克和4千克重量的物品时,弹簧长度为多少?学生得出的答案分别为6.8厘米和7.4厘米. 最后教师提出要求:“那么请同学们利用我们刚刚学习的函数,构建函数关系式. ”学生经过分析,用x表示弹簧所挂物体的质量,y表示弹簧总长度,则y=0.6x+5. 学生刚刚接触函数,教师不能过于激进,要循序渐进,引导学生建模,从简单的情境出发,利用试验让其感受弹簧长度随物体质量变化而变化,激发其学习欲望,提升教学效率.
2. 通过观察,分析变化
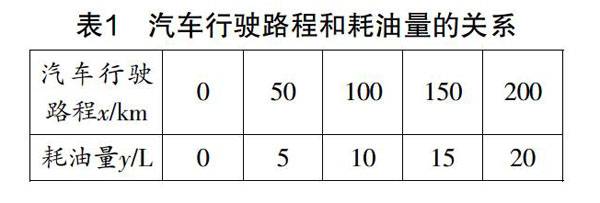
某小型轿车油箱中原有汽油50 L,每行驶50 km耗油5 L. 教师利用表格让学生回答问题,如表1. 学生通过计算,填出答案:0、5、10、15、20. 然后教师提问:“同学们请写出耗油量y和汽车行驶路程x的关系. ”学生的答案是y=0.1x,教师追问:“那么请同学们分析,剩余油量z和汽车行驶路程之间的关系是怎样的?”学生最终建立模型z=50-0.1x. 教师继续提问:“汽车可以无限行驶下去吗?”学生回答:“不能. ”教师:“行驶路程x的取值范围为多少?”学生分析:“汽车在还没有行驶的时候油箱中有50 L油,每行驶50 km耗油5 L,那么汽车行驶■×50=500(km)后,汽车油量全部消耗光,可见x不会无限增加,范围是0~500 km.”最终构建模型为y=0.1x(0≤x≤500);z=50-0.1x(0≤x≤500). 在之前创建情境的基础上,教师就可尝试将课堂交给学生,独立完成构建模型、解答和验证模型,并计算x取值范围,构建完整模型. 这样的过程能够培养学生学习的细心和严谨,解答问题更加周全,促进将来学习和生活的准确性.
■
3. 回顾反思,总结模型
当教学结束后,教师带领学生进行知识的回顾和总结,如通过问题“经过本节课的学习,请谈一谈你有何收获”引导学生独立回顾自己构建和解答模型后的收获和困惑,在与同学的交流中,教师适当给予提醒,令学生可以主动总结出模型构建的方法. 如果学生学习和接受一次函数知識需要一段时间,为了激发其思维,可以在发现问题环节多进行演示,让学生在实际情境中分析数学问题,教师根据其知识接受能力给予精准指导,建立一次函数模型,并通过对一次函数的探索,为后期学习奠定基础,帮助学生养成良好的学习习惯.
综上所述,构建模型是初中函数教学的主要内容,可以帮助学生解答更加复杂的问题. 特别是一次函数教学过程中,将之前用数字代表的关系式,转化为字母形式. 并通过提出质疑、提出假设、构建模型、答疑解惑和最终验证模型,帮助学生提升学习效率.

