指挥信息系统通信网络拓扑结构分析研究
杨帆+杨欣

摘 要:应用复杂网络理论,对指挥信息系统通信网络拓扑结构进行了分析研究。本文将指挥信息系统通信网络抽象为节点和边组成的简单网络图,提出了随机点攻击和智能点攻击两种抗毁性测试方法,建立了通信网络可靠性量化计算方法,对系统通信网络进行了仿真计算。结论验证了该方法的合理性,从拓扑结构分析的角度为指挥信息系统通信网络的风险分析奠定了基础、开辟了蹊径。
关键词:指挥信息系统;通信网络;拓扑分析
指挥信息系统,主要为各级防空指挥员及指挥机关遂行防空作战指挥任务提供自动化的指挥控制平台。
通信网络是指挥信息系统各分系统组网运行的基础,是指控、情报等要素的重点保障。研究指挥信息系统通信网络的拓扑结构,对于分析装备使用过程中的风险点,使装备的使用风险最小、效能最大,对提高基于指挥信息系统的体系作战能力有着重要意义。
复杂网络就是具有复杂拓扑结构和动力行为的大规模网络。从复杂网络的定义,可以得出所要研究的该装备通信网络也是一个典型的复杂网络。因为该通信网由大量的节点所组成,且每个节点具有自身动力学特征,每个节点不是独立存在的,它们与其他节点具有相互连接、相互作用的特点,从而整个通信网具有非常复杂的动力学特征。故该装备的通信网络作为一个典型的复杂网络,用复杂网络理论对它进行可靠性研究是科学有效的。
本文对该装备的通信网拓扑结构进行分析,为该装备的通信网风险管理做基础性研究。
1 基本定义及通信网络拓扑分析模型
1.1 复杂网络的定义
复杂网络就是具有复杂拓扑结构和动力行为的大规模网络。就目前的研究成果而言,一般从图论和矩阵两种方式定义复杂网络。
从图论的方面出发,假设网络中存在n个节点和m条连接线,则可以定义节点集合V={v1,v2,v3,…vn}和边集E={e1,e2,e3,…em}来表示这个网络,其中的边可以有方向和无方向两种,为了简化计算,只考虑无向图。图1是一个网络图示例,它有5个节点和4条连接这些节点的边,可以将它视为端集V={1,2,3,4,5},边集E={e12,e15,e23,e25},其中节点4为独立节点。
从矩阵的角度出发,最常用的就是用一个邻接矩阵A来表示网络的图的结构信息,如果网络中的i节点和j节点是相互连接的,则矩阵上相应位置上Aij的数值为1,如果这两点之间不存在连接边,则相应的Aij的数值就为0,显然一个无向图的邻接矩阵式一个对称矩阵。为了方便对复杂网络的同步特性的研究,本文用比较特殊的对称邻接矩阵表示所对应的网络。
对角线上元素Aij=。对于图1的矩阵表示为
复杂网络的可靠性定义为:在自然或者人为的破坏下,复杂网络自身能够保持原有功能的能力。
从复杂网络的定义可以看出,包括了可靠性的研究对象、规定条件、原有功能着三个要素。首先研究对象就是:具有数量级大的节点和边的复杂网络,且这些节点具有非线性动力性、还要具有按照一定网络拓扑渐渐演化的过程。规定的条件:自然或认为的破坏作用,这里主要是指对网络中的节点和边进行随机攻击或者进行智能攻击。保持原有功能的能力指的是:复杂网络的存在都是为了完成现实中的一些客观存在的功能,如果对这些网络进行了随机攻击和智能攻击后,会对原来的网络造成一定的影响,然而在这种情况下,复杂网络仍然能够保持或者部分保持实现某一功能的能力。
1.2 指挥信息系统通信网络模型
为了计算的方便我们将导弹营、高炮营配属数量减半并简化,将节点编号如图3:
从网络拓扑的简化结构图可以看出节点对之间的连接关系,可以将它表示为
端集V={1,2,3,…,13},
边集E={e12,e13,e14,e15,e16,e23,e24,e25,e28,e29,e2,10,e34,e35,e3,11,e3,12,e3,13,e45,e47}的图。
2 复杂网络的描述参数
复杂网络的描述参数有助于我们对网络的内部特征深入了解,描述参数有:网络的度、网络的聚集系数、网络的最短路径和耦合矩阵特征值。
2.1 节点的度
节点度数ki是第i个节点连接的边数目,即相当于i点的所有相邻节点的数目。在物理学领域中,节点的度表示本地的网络连接的连通性。通过邻接矩阵可以很简单地推出度ki的值:
节点的度分布是一个扩展的节点的度的概念。用分布函数P(k)来表示度的分布,P(k)是网络中某个节点具有k条边或k个邻接点的概率。网络的全局连通性和节点在网络中的重要性都靠节点度的分布,所以它是整个网络的基本统计特征,它同样可以表征网络的均匀性特征。复杂网络的平均度也是一个很重要的概念,平均度这里用表示:
网络的平均度是用来表征整个网络上的所有节点的平均度的数值,同样也可以来衡量网络的疏密程度,越大,对应的网络就越密集,越小,网络就越稀疏。
2.2 最短路径
我们将网络中某一节点到达另一节点所要经过的距离定义为路径长度,在本文中就是指节点直接相互连接所需要的边的数目。最短路径长度lij表示的是节点i到节点j的最短距离,即经过的最少的边的数目。从上述定义可以得出,最短路径长度是以边长作为单位的拓扑距离。与平均节点度概念类似,也存在平均最短路径长度L的概念,它表示的是图的任意两点的最短路集合{lij}的平均值。最短路径长度L的数值可以表征网络的特征尺寸,可以表征网络的连通度。
2.3 聚集系数
我们将图中某一节点的两个最近邻也是近邻的概率定义为聚集系数C。设点i的数目为Ei,k表示这些近邻点与i之间有连线的数目。则定义节点i的聚集系数为:
节点i附近环境的连通性用聚集系数Ci来表示。对网络上全部节点Ci进行平均计算得到的C即为平均聚集系数,整个网络的连通性用C来衡量。
2.4 耦合矩阵特征值
耦合矩阵的特征值是用来表征网络同步特性的重要参数,复杂网络的同步特征是一个重要的属性,反映复杂网络同步特征的参数就是耦合矩阵的特征值。
对于图3,可以得到每个节点的节点度,如k1=5,k2=7,则该网络的平均节点度=2.77,从平均节点度可以看出,该网络的密集程度不高。
3 网络的点攻击设计
为了对网络可靠性进行评价,首先要对网络进行攻击,本文中,分别对网络进行随机攻击和智能攻击,从而评价一个网络所能承受攻击的能力,为网络可靠性的评定提供依据。
3.1 随机攻击
随机攻击就是对网络中的点进行随机的撤除或对该节点的连接线进行随机的切断。在现实中可能发生的事故是由于网络自身的故障,而引起某个或部分节点失效。只要对网络相应的邻接矩阵中的某行和列进行随机的置零就完成了。
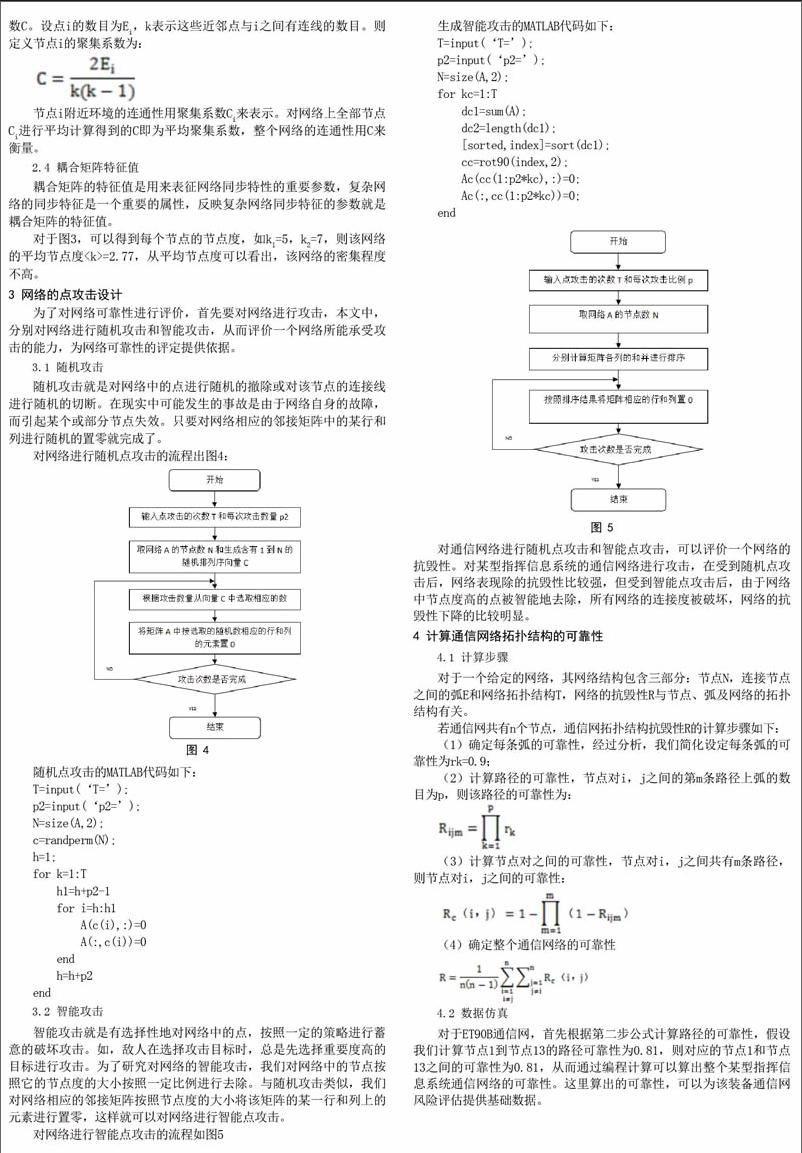
对网络进行随机点攻击的流程出图4:
随机点攻击的MATLAB代码如下:
T=input(‘T=);
p2=input(‘p2=);
N=size(A,2);
c=randperm(N);
h=1;
for k=1:T
h1=h+p2-1
for i=h:h1
A(c(i),:)=0
A(:,c(i))=0
end
h=h+p2
end
3.2 智能攻击
智能攻击就是有选择性地对网络中的点,按照一定的策略进行蓄意的破坏攻击。如,敌人在选择攻击目标时,总是先选择重要度高的目标进行攻击。为了研究对网络的智能攻击,我们对网络中的节点按照它的节点度的大小按照一定比例进行去除。与随机攻击类似,我们对网络相应的邻接矩阵按照节点度的大小将该矩阵的某一行和列上的元素进行置零,这样就可以对网络进行智能点攻击。
对网络进行智能点攻击的流程如图5
生成智能攻击的MATLAB代码如下:
T=input(‘T=);
p2=input(‘p2=);
N=size(A,2);
for kc=1:T
dc1=sum(A);
dc2=length(dc1);
[sorted,index]=sort(dc1);
cc=rot90(index,2);
Ac(cc(1:p2*kc),:)=0;
Ac(:,cc(1:p2*kc))=0;
end
对通信网络进行随机点攻击和智能点攻击,可以评价一个网络的抗毁性。对某型指挥信息系统的通信网络进行攻击,在受到随机点攻击后,网络表现除的抗毁性比较强,但受到智能点攻击后,由于网络中节点度高的点被智能地去除,所有网络的连接度被破坏,网络的抗毁性下降的比较明显。
4 计算通信网络拓扑结构的可靠性
4.1 计算步骤
对于一个给定的网络,其网络结构包含三部分:节点N,连接节点之间的弧E和网络拓扑结构T,网络的抗毁性R与节点、弧及网络的拓扑结构有关。
若通信网共有n个节点,通信网拓扑结构抗毁性R的计算步骤如下:
(1)确定每条弧的可靠性,经过分析,我们简化设定每条弧的可靠性为rk=0.9;
(2)计算路径的可靠性,节点对i,j之间的第m条路径上弧的数目为p,则该路径的可靠性为:
(3)计算节点对之间的可靠性,节点对i,j之间共有m条路径,则节点对i,j之间的可靠性:
(4)确定整个通信网络的可靠性
4.2 数据仿真
对于ET90B通信网,首先根据第二步公式计算路径的可靠性,假设我们计算节点1到节点13的路径可靠性为0.81,则对应的节点1和节点13之间的可靠性为0.81,从而通过编程计算可以算出整个某型指挥信息系统通信网络的可靠性。这里算出的可靠性,可以为该装备通信网风险评估提供基础数据。
5 结语
利用复杂网络理论对某型指挥信息系统通信网络进行分析,可以简化网络模型,将通信网络抽象为只有节点与连接线的图,对网络进行随机点攻击和智能点攻击,来评价网络受到这两种攻击下抗毁性的变化,针对规程给出的拓扑可靠性计算步骤,对某型指挥信息系统通信网络拓扑的可靠性进行仿真计算,可以看出,该装备通信网络密集程度不高,拓扑结构较为可靠,但抗毁性不强,为该装备通信网风险评估相关研究开辟了蹊径、提供网络拓扑可靠性的基础数据。
参考文献
[1]杨丽徙,曾新梅,方华强,娄北,张鸿雁,李珂.基于抗毁性分析的中压配电网络拓扑结构.电力系统自动化,2013.4
[2]高会生.电力通信网可靠性研究.华北电力大学.2009
[3]肖龙.网络通信系统的风险分析与评估.四川大学.2003
[4]张进. 基于复杂性的指挥信息系统通信网络组织建立阶段风险管理.火力与指挥控制.2014.4
[5]赵子岩,刘建明. 基于业务风险均衡度的电力通信网可靠性评估算法.电网技术.2011.10
[6]胡英. 网络通信系统的风险分析及评估.信息通信.2015.4


摘 要:应用复杂网络理论,对指挥信息系统通信网络拓扑结构进行了分析研究。本文将指挥信息系统通信网络抽象为节点和边组成的简单网络图,提出了随机点攻击和智能点攻击两种抗毁性测试方法,建立了通信网络可靠性量化计算方法,对系统通信网络进行了仿真计算。结论验证了该方法的合理性,从拓扑结构分析的角度为指挥信息系统通信网络的风险分析奠定了基础、开辟了蹊径。
关键词:指挥信息系统;通信网络;拓扑分析
指挥信息系统,主要为各级防空指挥员及指挥机关遂行防空作战指挥任务提供自动化的指挥控制平台。
通信网络是指挥信息系统各分系统组网运行的基础,是指控、情报等要素的重点保障。研究指挥信息系统通信网络的拓扑结构,对于分析装备使用过程中的风险点,使装备的使用风险最小、效能最大,对提高基于指挥信息系统的体系作战能力有着重要意义。
复杂网络就是具有复杂拓扑结构和动力行为的大规模网络。从复杂网络的定义,可以得出所要研究的该装备通信网络也是一个典型的复杂网络。因为该通信网由大量的节点所组成,且每个节点具有自身动力学特征,每个节点不是独立存在的,它们与其他节点具有相互连接、相互作用的特点,从而整个通信网具有非常复杂的动力学特征。故该装备的通信网络作为一个典型的复杂网络,用复杂网络理论对它进行可靠性研究是科学有效的。
本文对该装备的通信网拓扑结构进行分析,为该装备的通信网风险管理做基础性研究。
1 基本定义及通信网络拓扑分析模型
1.1 复杂网络的定义
复杂网络就是具有复杂拓扑结构和动力行为的大规模网络。就目前的研究成果而言,一般从图论和矩阵两种方式定义复杂网络。
从图论的方面出发,假设网络中存在n个节点和m条连接线,则可以定义节点集合V={v1,v2,v3,…vn}和边集E={e1,e2,e3,…em}来表示这个网络,其中的边可以有方向和无方向两种,为了简化计算,只考虑无向图。图1是一个网络图示例,它有5个节点和4条连接这些节点的边,可以将它视为端集V={1,2,3,4,5},边集E={e12,e15,e23,e25},其中节点4为独立节点。
从矩阵的角度出发,最常用的就是用一个邻接矩阵A来表示网络的图的结构信息,如果网络中的i节点和j节点是相互连接的,则矩阵上相应位置上Aij的数值为1,如果这两点之间不存在连接边,则相应的Aij的数值就为0,显然一个无向图的邻接矩阵式一个对称矩阵。为了方便对复杂网络的同步特性的研究,本文用比较特殊的对称邻接矩阵表示所对应的网络。
对角线上元素Aij=。对于图1的矩阵表示为
复杂网络的可靠性定义为:在自然或者人为的破坏下,复杂网络自身能够保持原有功能的能力。
从复杂网络的定义可以看出,包括了可靠性的研究对象、规定条件、原有功能着三个要素。首先研究对象就是:具有数量级大的节点和边的复杂网络,且这些节点具有非线性动力性、还要具有按照一定网络拓扑渐渐演化的过程。规定的条件:自然或认为的破坏作用,这里主要是指对网络中的节点和边进行随机攻击或者进行智能攻击。保持原有功能的能力指的是:复杂网络的存在都是为了完成现实中的一些客观存在的功能,如果对这些网络进行了随机攻击和智能攻击后,会对原来的网络造成一定的影响,然而在这种情况下,复杂网络仍然能够保持或者部分保持实现某一功能的能力。
1.2 指挥信息系统通信网络模型
为了计算的方便我们将导弹营、高炮营配属数量减半并简化,将节点编号如图3:
从网络拓扑的简化结构图可以看出节点对之间的连接关系,可以将它表示为
端集V={1,2,3,…,13},
边集E={e12,e13,e14,e15,e16,e23,e24,e25,e28,e29,e2,10,e34,e35,e3,11,e3,12,e3,13,e45,e47}的图。
2 复杂网络的描述参数
复杂网络的描述参数有助于我们对网络的内部特征深入了解,描述参数有:网络的度、网络的聚集系数、网络的最短路径和耦合矩阵特征值。
2.1 节点的度
节点度数ki是第i个节点连接的边数目,即相当于i点的所有相邻节点的数目。在物理学领域中,节点的度表示本地的网络连接的连通性。通过邻接矩阵可以很简单地推出度ki的值:
节点的度分布是一个扩展的节点的度的概念。用分布函数P(k)来表示度的分布,P(k)是网络中某个节点具有k条边或k个邻接点的概率。网络的全局连通性和节点在网络中的重要性都靠节点度的分布,所以它是整个网络的基本统计特征,它同样可以表征网络的均匀性特征。复杂网络的平均度也是一个很重要的概念,平均度这里用
网络的平均度是用来表征整个网络上的所有节点的平均度的数值,同样也可以来衡量网络的疏密程度,
2.2 最短路径
我们将网络中某一节点到达另一节点所要经过的距离定义为路径长度,在本文中就是指节点直接相互连接所需要的边的数目。最短路径长度lij表示的是节点i到节点j的最短距离,即经过的最少的边的数目。从上述定义可以得出,最短路径长度是以边长作为单位的拓扑距离。与平均节点度概念类似,也存在平均最短路径长度L的概念,它表示的是图的任意两点的最短路集合{lij}的平均值。最短路径长度L的数值可以表征网络的特征尺寸,可以表征网络的连通度。
2.3 聚集系数
我们将图中某一节点的两个最近邻也是近邻的概率定义为聚集系数C。设点i的数目为Ei,k表示这些近邻点与i之间有连线的数目。则定义节点i的聚集系数为:
节点i附近环境的连通性用聚集系数Ci来表示。对网络上全部节点Ci进行平均计算得到的C即为平均聚集系数,整个网络的连通性用C来衡量。
2.4 耦合矩阵特征值
耦合矩阵的特征值是用来表征网络同步特性的重要参数,复杂网络的同步特征是一个重要的属性,反映复杂网络同步特征的参数就是耦合矩阵的特征值。
对于图3,可以得到每个节点的节点度,如k1=5,k2=7,则该网络的平均节点度
3 网络的点攻击设计
为了对网络可靠性进行评价,首先要对网络进行攻击,本文中,分别对网络进行随机攻击和智能攻击,从而评价一个网络所能承受攻击的能力,为网络可靠性的评定提供依据。
3.1 随机攻击
随机攻击就是对网络中的点进行随机的撤除或对该节点的连接线进行随机的切断。在现实中可能发生的事故是由于网络自身的故障,而引起某个或部分节点失效。只要对网络相应的邻接矩阵中的某行和列进行随机的置零就完成了。
对网络进行随机点攻击的流程出图4:
随机点攻击的MATLAB代码如下:
T=input(‘T=);
p2=input(‘p2=);
N=size(A,2);
c=randperm(N);
h=1;
for k=1:T
h1=h+p2-1
for i=h:h1
A(c(i),:)=0
A(:,c(i))=0
end
h=h+p2
end
3.2 智能攻击
智能攻击就是有选择性地对网络中的点,按照一定的策略进行蓄意的破坏攻击。如,敌人在选择攻击目标时,总是先选择重要度高的目标进行攻击。为了研究对网络的智能攻击,我们对网络中的节点按照它的节点度的大小按照一定比例进行去除。与随机攻击类似,我们对网络相应的邻接矩阵按照节点度的大小将该矩阵的某一行和列上的元素进行置零,这样就可以对网络进行智能点攻击。
对网络进行智能点攻击的流程如图5
生成智能攻击的MATLAB代码如下:
T=input(‘T=);
p2=input(‘p2=);
N=size(A,2);
for kc=1:T
dc1=sum(A);
dc2=length(dc1);
[sorted,index]=sort(dc1);
cc=rot90(index,2);
Ac(cc(1:p2*kc),:)=0;
Ac(:,cc(1:p2*kc))=0;
end
对通信网络进行随机点攻击和智能点攻击,可以评价一个网络的抗毁性。对某型指挥信息系统的通信网络进行攻击,在受到随机点攻击后,网络表现除的抗毁性比较强,但受到智能点攻击后,由于网络中节点度高的点被智能地去除,所有网络的连接度被破坏,网络的抗毁性下降的比较明显。
4 计算通信网络拓扑结构的可靠性
4.1 计算步骤
对于一个给定的网络,其网络结构包含三部分:节点N,连接节点之间的弧E和网络拓扑结构T,网络的抗毁性R与节点、弧及网络的拓扑结构有关。
若通信网共有n个节点,通信网拓扑结构抗毁性R的计算步骤如下:
(1)确定每条弧的可靠性,经过分析,我们简化设定每条弧的可靠性为rk=0.9;
(2)计算路径的可靠性,节点对i,j之间的第m条路径上弧的数目为p,则该路径的可靠性为:
(3)计算节点对之间的可靠性,节点对i,j之间共有m条路径,则节点对i,j之间的可靠性:
(4)确定整个通信网络的可靠性
4.2 数据仿真
对于ET90B通信网,首先根据第二步公式计算路径的可靠性,假设我们计算节点1到节点13的路径可靠性为0.81,则对应的节点1和节点13之间的可靠性为0.81,从而通过编程计算可以算出整个某型指挥信息系统通信网络的可靠性。这里算出的可靠性,可以为该装备通信网风险评估提供基础数据。
5 结语
利用复杂网络理论对某型指挥信息系统通信网络进行分析,可以简化网络模型,将通信网络抽象为只有节点与连接线的图,对网络进行随机点攻击和智能点攻击,来评价网络受到这两种攻击下抗毁性的变化,针对规程给出的拓扑可靠性计算步骤,对某型指挥信息系统通信网络拓扑的可靠性进行仿真计算,可以看出,该装备通信网络密集程度不高,拓扑结构较为可靠,但抗毁性不强,为该装备通信网风险评估相关研究开辟了蹊径、提供网络拓扑可靠性的基础数据。
参考文献
[1]杨丽徙,曾新梅,方华强,娄北,张鸿雁,李珂.基于抗毁性分析的中压配电网络拓扑结构.电力系统自动化,2013.4
[2]高会生.电力通信网可靠性研究.华北电力大学.2009
[3]肖龙.网络通信系统的风险分析与评估.四川大学.2003
[4]张进. 基于复杂性的指挥信息系统通信网络组织建立阶段风险管理.火力与指挥控制.2014.4
[5]赵子岩,刘建明. 基于业务风险均衡度的电力通信网可靠性评估算法.电网技术.2011.10
[6]胡英. 网络通信系统的风险分析及评估.信息通信.2015.4

